PC_2020-2_EP07_Paridade. Inversa. Crescimento_GABARITO.pdf

Pré-Cálculo 2020-2 EP 07 – GABARITO 1 de 21
DISCIPLINA PRÉ-CÁLCULO 2020-2
Profa. Maria Lúcia Campos
Profa. Marlene Dieguez
EP07 – Paridade, Função Inversa e Crescimento de Funções
GABARITO
____________________________________________________________________________
Exercício 1:
Dê o ponto simétrico dos pontos: I) 𝑃(1, 4) II) 𝑄(−2, 3) em relação:
a) ao eixo 𝑥 b) ao eixo 𝑦 c) à origem d) à reta 𝑦 = 𝑥.
RESOLUÇÃO:
I) 𝑃(1,4)
a) O ponto simétrico do ponto 𝑃(1, 4) em
relação ao eixo 𝑥 é o ponto (1, −4).
b) O ponto simétrico do ponto 𝑃( 1, 4) em
relação ao eixo 𝑦 é o ponto (−1, 4).
c) O ponto simétrico do ponto 𝑃( 1, 4) em
relação à origem é o ponto (−1, −4).
d) O ponto simétrico do ponto 𝑃(1, 4) em
relação à reta 𝑦 = 𝑥 é o ponto (4, 1).
------------------------------------------------------------------------------------------------------------------------------------------
II) 𝑄(−2, 3)
a) O ponto simétrico do ponto 𝑄(−2, 3) em relação
ao eixo 𝑥 , é o ponto (−2, −3).
b) O ponto simétrico do ponto 𝑄(−2, 3) em relação
ao eixo 𝑦 é o ponto (2, 3).
c) O ponto simétrico do ponto 𝑄(−2, 3) em relação à
origem é o ponto (2, −3).

d) O ponto simétrico do ponto 𝑄(−2, 3) em relação à reta
x
y = é o ponto (3, −2).
_____________________________________________________________________________________
Exercício 2:
a) Se o ponto (−
1
7
, −√3) estiver no gráfico de uma função par, 𝑓, que outro ponto também deverá
estar no gráfico?
b) E se este ponto estiver no gráfico de uma função ímpar, 𝑔, que outro ponto também deverá estar no
gráfico?
RESOLUÇÃO:
a) Se a função f é par então 𝑓(−𝑥) = 𝑓(𝑥) . Logo, 𝑓 (
1
7
) = 𝑓 (−
1
7
) . Como (−
1
7
, −√3) está no
gráfico da função f , então 𝑓 (−
1
7
) = −√3 e 𝑓 (
1
7
) = 𝑓 (−
1
7
) = −√3. Concluímos então, que o par
ordenado (
1
7
, −√3) também está no gráfico da função par, 𝑓.
-----------------------------------------------------------------------------------------------------------------------------------------
b) Se a função 𝑔 é ímpar então 𝑔(−𝑥) = −𝑔(𝑥). Logo, 𝑔 (
1
7
) = −𝑔 (−
1
7
) = −(−√3) = √3 donde
concluímos, que o par ordenado (
𝟏
𝟕
, √𝟑) também está no gráfico da função ímpar, 𝑔.
_____________________________________________________________________________________
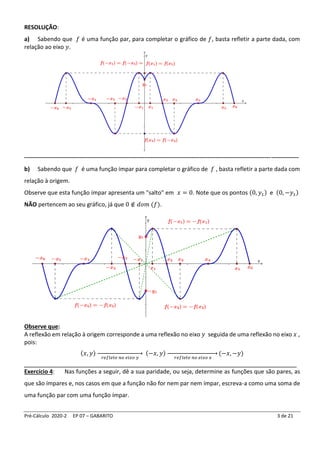
Exercício 3:
Uma função 𝑓 tem domínio [−𝑥6, 𝑥6] e a
parte do seu gráfico para 𝑥 ∈ [0, 𝑥6]
está mostrada ao lado.
a) Complete o gráfico de 𝑓 supondo que ela é uma função par e 𝑓(0) = 𝑦1.
b) Complete o gráfico de 𝑓 supondo que ela é uma função ímpar e 0 ∉ 𝑑𝑜𝑚 (𝑓).

RESOLUÇÃO:
a) Sabendo que 𝑓 é uma função par, para completar o gráfico de 𝑓, basta refletir a parte dada, com
relação ao eixo 𝑦.
-------------------------------------------------------------------------------------------------------------------------------------------
b) Sabendo que 𝑓 é uma função ímpar para completar o gráfico de 𝑓 , basta refletir a parte dada com
relação à origem.
Observe que esta função ímpar apresenta um "salto" em 𝑥 = 0. Note que os pontos (0, 𝑦1) e (0, −𝑦1)
NÃO pertencem ao seu gráfico, já que 0 ∉ 𝑑𝑜𝑚 (𝑓).
Observe que:
A reflexão em relação à origem corresponde a uma reflexão no eixo 𝑦 seguida de uma reflexão no eixo 𝑥 ,
pois:
(𝑥, 𝑦)
𝑟𝑒𝑓𝑙𝑒𝑡𝑒 𝑛𝑜 𝑒𝑖𝑥𝑜 𝑦
→ (−𝑥, 𝑦)
𝑟𝑒𝑓𝑙𝑒𝑡𝑒 𝑛𝑜 𝑒𝑖𝑥𝑜 𝑥
→ (−𝑥, −𝑦)
____________________________________________________________________________
Exercício 4: Nas funções a seguir, dê a sua paridade, ou seja, determine as funções que são pares, as
que são ímpares e, nos casos em que a função não for nem par nem ímpar, escreva-a como uma soma de
uma função par com uma função ímpar.

a) 𝑓(𝑥) = 5𝑥7
− 3𝑥4
+
1
4
𝑥3
+ 7𝑥 − 6 b) 𝑔(𝑥) = √2|𝑥| − 𝑥4
c) ℎ(𝑥) =
2𝑥3
1−𝑥2
d) 𝑗(𝑥) =
𝑥
1+𝑥2
+ 𝑥6
+ √𝑥2 − 1
e) 𝑘(𝑥) = 5 − 𝑥3
√1 + 𝑥4 f) 𝑙(𝑥) = √𝑥 − 4
g) 𝑚(𝑥) = 𝑥
3
5 = √𝑥3
5
h) 𝑛(𝑥) = 𝑥
4
5 = √𝑥4
5
i) 𝑜(𝑥) = 𝑥
3
4 = √𝑥3
4
j) 𝑝(𝑥) = {
√−2 − 𝑥, 𝑥 ≤ −2
√−2 + 𝑥, 𝑥 ≥ 2
RESOLUÇÃO:
a) 𝐷𝑜𝑚(𝑓) = ℝ. ℝ é um conjunto simétrico em relação à origem da reta numérica.
A função 𝑓(𝑥) = 5𝑥7
− 3𝑥4
+
1
4
𝑥3
+ 7𝑥 − 6 é um polinômio e como apresenta monômios de grau par
e monômios de grau ímpar não é uma função par nem ímpar.
𝑓(−1) = 5(−1)7
− 3(−1)4
+
1
4
(−1)3
+ 7(−1) − 6 = −5 − 3 −
1
4
− 7 − 6 = −21 −
1
4
= −
85
4
𝑓(1) = 5(1)7
− 3(1)4
+
1
4
(1)3
+ 7(1) − 6 = 5 − 3 +
1
4
+ 7 − 6 = 3 +
1
4
=
13
4
Logo, como 𝑓(−1) ≠ 𝑓(1), 𝑓 não é par, e como 𝑓(−1) ≠ −𝑓(1), 𝑓 não é ímpar.
Portanto vamos escrevê-la como a soma de uma função par com uma função ímpar.
Defina,
𝑓𝑖(𝑥) = 5𝑥7
+
1
4
𝑥3
+ 7𝑥 e 𝑓
𝑝(𝑥) = −3𝑥4
− 6
Como 𝑓𝑖(−𝑥) = 5(−𝑥)7
+
1
4
(−𝑥)3
+ 7(−𝑥) = −𝑥7
−
1
4
𝑥3
− 7𝑥 = − (5𝑥7
+
1
4
𝑥3
+ 7𝑥) = −𝑓𝑖(𝑥),
então 𝑓𝑖 é uma função ímpar.
Como 𝑓𝑝(−𝑥) = −3(−𝑥)4
− 6 = −3𝑥4
− 6 = 𝑓
𝑝(𝑥) , então 𝑓
𝑝 é uma função par.
Portanto,
𝑓(𝑥) = 5𝑥7
− 3𝑥4
+
1
4
𝑥3
+ 7𝑥 − 6 = (5𝑥7
+
1
4
𝑥3
+ 7𝑥) + (−3𝑥4
− 6) = 𝑓𝑖(𝑥) + 𝑓
𝑝(𝑥).
-------------------------------------------------------------------------------------------------------------------------------------------
b) Seja 𝑔(𝑥) = √2|𝑥| − 𝑥4
. 𝐷𝑜𝑚(𝑓) = ℝ , pois 2|𝑥| ≥ 0, ∀𝑥 ∈ ℝ.
ℝ é um conjunto simétrico em relação à origem da reta numérica.
Como |−𝑥| = |𝑥| e (−𝑥)4
= 𝑥4
, temos que,
𝑔(−𝑥) = √2| − 𝑥| − (−𝑥)4
= √2|𝑥| − 𝑥4
= 𝑔(𝑥).
Donde, a função 𝑔 é uma função par.
-------------------------------------------------------------------------------------------------------------------------------------------
c) Seja ℎ(𝑥) =
2𝑥3
1−𝑥2
. Como o denominador deve ser diferente de zero, então, 1 − 𝑥2
≠ 0 donde,
𝑥 ≠ −1, portanto 𝐷𝑜𝑚(ℎ) = ℝ − {−1, 1}, que é um subconjunto simétrico em relação à origem da reta
numérica.
Sendo (−𝑥)2
= 𝑥2
e (−𝑥)3
= −(𝑥)3
, então,
(−𝑥) =
2(−𝑥)3
1−(−𝑥)2
=
−2𝑥3
1−𝑥2
=
−2(𝑥)3
1−(𝑥)2
= −
2(𝑥)3
1−(𝑥)2
= −ℎ(𝑥).
Donde, a função ℎ é uma função ímpar.
-------------------------------------------------------------------------------------------------------------------------------------------

d) Seja 𝑗(𝑥) =
𝑥
1+𝑥2 + 𝑥6
+ √𝑥2 − 1 . Para que a raiz quadrada √𝑥2 − 1 possa ser calculada, é preciso
que 𝑥2
− 1 ≥ 0 logo 𝑥 ≤ −1 ou 𝑥 ≥ 1. Portanto 𝐷𝑜𝑚(𝑗) = (−∞, −1] ∪ [1, ∞), que é um subconjunto
simétrico em relação à origem da reta numérica.
𝑗(𝑥) =
−𝑥
1+(−𝑥)2
+ (−𝑥)6
+ √(−𝑥)2 − 1 =
−𝑥
1+𝑥2
+ 𝑥6
+ √𝑥2 − 1 = −
𝑥
1+𝑥2
+ 𝑥6
+ √𝑥2 − 1.
Esta equação mostra que a função j não é par nem ímpar. Portanto vamos escrevê-la como a soma de
uma função par com uma função ímpar.
Defina:
𝑗𝑖(𝑥) =
𝑥
1+𝑥2 e 𝑗𝑝(𝑥) = 𝑥6
+ √𝑥2 − 1
Vemos que,
𝑗𝑖(−𝑥) =
−𝑥
1+(−𝑥)2
=
−𝑥
1+𝑥2
= −
𝑥
1+𝑥2
= −𝑗𝑖(𝑥), donde concluímos que a função 𝑗𝑖 é uma função ímpar e
𝑗𝑝(−𝑥) = (−𝑥)6
+ √(−𝑥)2 − 1 = 𝑥6
+ √𝑥2 − 1 = 𝑗𝑝(𝑥), donde concluímos que a função 𝑗𝑝 é uma
função par.
Portanto,
𝑗(𝑥) =
𝑥
1+𝑥2 + 𝑥6
+ √𝑥2 − 1 = (
𝑥
1+𝑥2) + (𝑥6
+ √𝑥2 − 1) = 𝑗𝑖(𝑥) + 𝑗𝑝(𝑥).
-------------------------------------------------------------------------------------------------------------------------------------------
e) Seja 𝑘(𝑥) = 5 − 𝑥3
√1 + 𝑥4. 𝐷𝑜𝑚(𝑘) = ℝ , pois 1 + 𝑥4
≥ 0, ∀𝑥 ∈ ℝ.
𝑘(𝑥) = 5 − (−𝑥)3
√1 + (−𝑥)4 = 5 + 𝑥3
√1 + 𝑥4.
Esta equação mostra que a função 𝑘 não é par nem ímpar. Portanto vamos escrevê-la como a soma de
uma função par com uma função ímpar. Lembre-se que essa decomposição é única.
Embora, depois dos exemplos feitos acima, não seja difícil descobrir a decomposição da função 𝑘 como
a soma de uma função par com uma função ímpar, vamos nesse exemplo, usar o fato lembrado no início
desse EP que diz,
𝑘(𝑥) =
𝑘(𝑥)+𝑘(−𝑥)
2
+
𝑘(𝑥)−𝑘(−𝑥)
2
= 𝑘𝑝(𝑥) + 𝑘𝑖(𝑥)
Assim,
𝑘𝑝(𝑥) =
𝑘(𝑥)+𝑘(−𝑥)
2
=
(5−𝑥3√1+𝑥4)+(5+𝑥3√1+𝑥4)
2
=
10
2
= 5.
𝑘𝑖(𝑥) =
𝑘(𝑥)−𝑘(−𝑥)
2
=
(5−𝑥3√1+𝑥4)−(5+𝑥3√1+𝑥4)
2
= −𝑥3
√1 + 𝑥4.
Portanto, 𝑘(𝑥) = 5 − 𝑥3
√1 + 𝑥4 = 5 + (−𝑥3
√1 + 𝑥4) = 𝑘𝑝(𝑥) + 𝑘𝑖(𝑥).
-------------------------------------------------------------------------------------------------------------------------------------------

f) 𝑙(𝑥) = √𝑥 − 4
Para que a raiz quadrada √𝑥 − 4 possa ser calculada, é preciso que 𝑥 − 4 ≥ 0, logo 𝑥 ≥ 4. Portanto
𝐷𝑜𝑚(𝑙) = [4, ∞), que não é um subconjunto simétrico em relação à origem da reta numérica. Portanto
𝑙(𝑥) = √𝑥 − 4 não pode ser analisada para função par, nem para função ímpar, nem ser escrita como
soma de uma função par com uma função ímpar.
-------------------------------------------------------------------------------------------------------------------------------------------
g) 𝑚(𝑥) = 𝑥
3
5 = √𝑥3
5
A raiz √𝑥3
5
pode ser calculada para ∀𝑥 ∈ ℝ, pois é uma raiz de índice ímpar. Logo 𝐷𝑜𝑚(𝑚) = ℝ.
𝑚(−𝑥) = (−𝑥)
3
5 = √(−𝑥)3
5
= √−𝑥3
5
= −√𝑥3
5
= −𝑚(𝑥) . Portanto, 𝑚(𝑥) = 𝑥
3
5 = √𝑥3
5
é uma função
ímpar.
-------------------------------------------------------------------------------------------------------------------------------------------
h) 𝑛(𝑥) = 𝑥
4
5 = √𝑥4
5
A raiz √𝑥4
5
pode ser calculada para ∀𝑥 ∈ ℝ , pois é uma raiz de índice ímpar. Logo 𝐷𝑜𝑚(𝑛) = ℝ.
𝑛(−𝑥) = (−𝑥)
4
5 = √(−𝑥)4
5
= √𝑥4
5
= 𝑛(𝑥) . Portanto, 𝑛(𝑥) = 𝑥
4
5 = √𝑥4
5
é uma função par.
-------------------------------------------------------------------------------------------------------------------------------------------
i) 𝑜(𝑥) = 𝑥
3
4 = √𝑥3
4
.
Para que a raiz √𝑥3
4
possa ser calculada, é preciso que 𝑥3
≥ 0 ⟹ 𝑥 ≥ 0, pois é uma raiz de índice par.
Logo 𝐷𝑜𝑚(𝑜) = [0, ∞), que não é um subconjunto simétrico em relação à origem da reta numérica.
Portanto 𝑜(𝑥) = 𝑥
3
4 = √𝑥3
4
não pode ser analisada para função par, nem para função ímpar, nem ser
escrita como soma de uma função par com uma função ímpar..
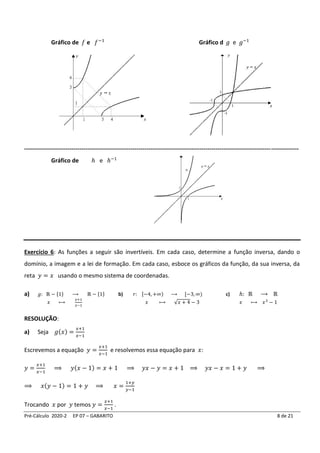
j) 𝑝(𝑥) = {
√−2 − 𝑥, 𝑥 ≤ −2
√−2 + 𝑥, 𝑥 ≥ 2
𝐷𝑜𝑚(𝑝) = (−∞, −2] ∪ [2, ∞) é um conjunto simétrico em relação à origem da reta numérica.
• Para 𝑥 ≥ 2 ⟹ −𝑥 ≤ −2 . Calculando 𝑝(𝑥) e 𝑝(−𝑥).
𝑥 ≥ 2 ⟹ 𝑝(𝑥) = √−2 + 𝑥 (*)
−𝑥 ≤ −2 ⟹ 𝑝(−𝑥) = √−2 − (−𝑥) = √−2 + 𝑥 (**)
Por (*) e (**), concluímos que 𝑥 ≥ 2 ⟹ 𝑝(−𝑥) = √−2 + 𝑥 = 𝑝(𝑥).
• Para 𝑥 ≤ −2 ⟹ −𝑥 ≥ 2 . Calculando 𝑝(𝑥) e 𝑝(−𝑥).
𝑥 ≤ −2 ⟹ 𝑝(𝑥) = √−2 − 𝑥 (***)

−𝑥 ≥ 2 ⟹ 𝑝(−𝑥) = √−2 + (−𝑥) = √−2 − 𝑥 (****)
Por (***) e (****), concluímos que 𝑥 ≤ −2 ⟹ 𝑝(−𝑥) = √−2 − 𝑥 = 𝑝(𝑥).
Assim, para ∀𝑥 ∈ 𝐷𝑜𝑚(𝑝) provamos que 𝑝(−𝑥) = 𝑝(𝑥).
Conclusão: a função 𝑝(𝑥) é uma função par.
____________________________________________________________________________
Exercício 5: As figuras a seguir representam gráficos de funções. Identifique entre elas aquelas que
representam gráficos de funções invertíveis e, nestes casos, esboce sobre a própria figura o gráfico da
função inversa
Gráfico de 𝑓 Gráfico de 𝑔
-------------------------------------------------------------------------------------------------------------------------------------------
Gráfico de ℎ Gráfico de 𝑗
RESOLUÇÃO:
A única função que não é invertível é a função 𝑗, pois ela não é uma função um a um. Basta observar que
ela não satisfaz o Teste da Reta Horizontal.
As funções 𝑓, 𝑔, ℎ satisfazem o Teste da Reta Horizontal e são, portanto, funções um a um e
consequentemente, invertíveis.
Vamos esboçar os gráficos dessas funções e das suas inversas no mesmo sistema de coordenadas.

Gráfico de 𝑓 e 𝑓−1
Gráfico d 𝑔 e 𝑔−1
-------------------------------------------------------------------------------------------------------------------------------------------
Gráfico de ℎ e ℎ−1
Exercício 6: As funções a seguir são invertíveis. Em cada caso, determine a função inversa, dando o
domínio, a imagem e a lei de formação. Em cada caso, esboce os gráficos da função, da sua inversa, da
reta 𝑦 = 𝑥 usando o mesmo sistema de coordenadas.
a) 𝑔: ℝ − {1} ⟶ ℝ − {1} b) 𝑟: [−4, +∞) ⟶ [−3, ∞) c) ℎ: ℝ ⟶ ℝ
𝑥 ⟼
𝑥+1
𝑥−1
𝑥 ⟼ √𝑥 + 4 − 3 𝑥 ⟼ 𝑥3
− 1
RESOLUÇÃO:
a) Seja 𝑔(𝑥) =
𝑥+1
𝑥−1
Escrevemos a equação 𝑦 =
𝑥+1
𝑥−1
e resolvemos essa equação para 𝑥:
𝑦 =
𝑥+1
𝑥−1
⟹ 𝑦(𝑥 − 1) = 𝑥 + 1 ⟹ 𝑦𝑥 − 𝑦 = 𝑥 + 1 ⟹ 𝑦𝑥 − 𝑥 = 1 + 𝑦 ⟹
⟹ 𝑥(𝑦 − 1) = 1 + 𝑦 ⟹ 𝑥 =
1+𝑦
𝑦−1
Trocando 𝑥 por 𝑦 temos 𝑦 =
𝑥+1
𝑥−1
.

Logo, 𝑔−1(𝑥) =
𝑥+1
𝑥−1
= 𝑔(𝑥) e 𝑔−1
: ℝ − {1} ⟶ ℝ − {1}
Vamos esboçar os gráficos de 𝑦 = 𝑔(𝑥) e 𝑔−1
(𝑥) no mesmo sistema de coordenadas:
Para construir o gráfico de 𝑦 =
𝑥+1
𝑥−1
precisamos simplificar a expressão, fazendo uma divisão de
polinômios ou somando e subtraindo 1 no numerador, com a intenção de simplificar até chegar a uma
expressão que possamos reconhecer como uma transformação sobre uma função elementar cujo gráfico
conhecemos. Façamos isso,
𝑦 =
𝑥+1
𝑥−1
=
𝑥−1+1+1
𝑥−1
=
𝑥−1+2
𝑥−1
=
𝑥−1
𝑥−1
+
2
𝑥−1
= 1 +
2
𝑥−1
O gráfico dessa função pode ser obtido pela seguinte sequência de transformações em gráficos:
𝑦 =
1
𝑥
(1)
→ 𝑦 =
2
𝑥
(2)
→ 𝑦 =
2
𝑥−1
(3)
→ 𝑦 = 1 +
2
𝑥−1
(1) Esticamento do gráfico da função elementar 𝑦 =
1
𝑥
por
um fator multiplicativo 2 .
(2) Translação horizontal de 1 unidade para a direita do
gráfico de 𝑦 =
2
𝑥
.
(3) Translação vertical de 1 unidade para cima do gráfico de
𝑦 =
2
𝑥−1
.
OBSERVE: Já vimos anteriormente que 𝑔−1(𝑥) =
𝑥+1
𝑥−1
= 𝑔(𝑥). Se tivéssemos iniciado o exercício
esboçando o gráfico de 𝑔, poderíamos tirar essa conclusão do próprio gráfico, já que o gráfico de 𝑔 é
simétrico em relação à reta 𝑦 = 𝑥.
-------------------------------------------------------------------------------------------------------------------------------------------
b) Seja 𝑟(𝑥) = √𝑥 + 4 − 3.
Escrevemos a equação 𝑦 = √𝑥 + 4 − 3 e resolvemos essa equação para 𝑥 :
𝑦 = √𝑥 + 4 − 3 ⟹ 𝑦 + 3 = √𝑥 + 4 ⟹ (𝑦 + 3)2
= 𝑥 + 4 ⟹ 𝑥 = (𝑦 + 3)2
− 4
Trocando 𝑥 por 𝑦 temos 𝑦 = (𝑥 + 3)2
− 4.
Logo, 𝑟−1(𝑥) = (𝑥 + 3)2
− 4 e 𝑟−1
: [−3, +∞) ⟶ [−4, +∞).
Esboçando os gráficos de 𝑦 = 𝑟(𝑥) = √𝑥 + 4 − 3 e 𝑦 = 𝑟−1(𝑥) = (𝑥 + 3)2
− 4 no mesmo sistema
de coordenadas:

O gráfico de 𝑦 = 𝑟−1(𝑥) = (𝑥 + 3)2
− 4 é a parte
do gráfico da parábola de vértice (−3, −4),
apenas para valores de 𝑥 ≥ −3, não devemos
desenhar toda a parábola.
-------------------------------------------------------------------------------------------------------------------------------------------
c) Seja ℎ(𝑥) = 𝑥3
− 1.
Escrevemos a equação 𝑦 = 𝑥3
− 1 e resolvemos essa equação para 𝑥:
𝑦 = 𝑥3
− 1 ⟹ 𝑦 + 1 = 𝑥3
𝑥 = √𝑦 + 1
3
.
Trocando 𝑥 por 𝑦 temos 𝑦 = √𝑥 + 1
3
.
Logo, ℎ−1(𝑥) = √𝑥 + 1
3
e ℎ−1
: ℝ ⟶ ℝ
Esboçando os gráficos de
𝑦 = ℎ(𝑥) = 𝑥3
− 1 e 𝑦 = ℎ−1(𝑥) = √𝑥 + 1
3
no mesmo sistema de coordenadas:
_____________________________________________________________________________________
Exercício 7: Seja 𝑓: (−∞, 0] ⟶ [1, +∞)
𝑥 ⟼ 𝑥2
+ 1
a) Determine a inversa 𝑓−1
e verifique que (𝑓 ∘ 𝑓−1)(𝑥) = (𝑓−1
∘ 𝑓)(𝑥).
b) Esboce os gráficos de 𝑓, 𝑓−1
, 𝑦 = 𝑥 usando o mesmo sistema de coordenadas.
RESOLUÇÃO:
Sabemos que 𝐷𝑜𝑚(𝑓−1) = 𝐼𝑚(𝑓) e 𝐼𝑚(𝑓−1) = 𝐷𝑜𝑚(𝑓), portanto:
𝐷𝑜𝑚(𝑓−1) = [1, +∞) e 𝐼𝑚(𝑓−1) = (−∞, 0].
Escrevemos 𝑦 = 𝑥2
+ 1 e resolvemos essa equação para 𝑥:
𝑦 = 𝑥2
+ 1 ⟹ 𝑥2
= 𝑦 − 1 ⟹ √𝑥2 = √𝑦 − 1 ⟹ |𝑥| = √𝑦 − 1
⟹ 𝑥 = √𝑦 − 1 ou 𝑥 = −√𝑦 − 1.
Trocando 𝑥 por 𝑦 temos 𝑦 = √𝑥 − 1 ou 𝑦 = −√𝑥 − 1.

Como 𝐼𝑚(𝑓−1) = (−∞, 0] então 𝑦 ≤ 0 e assim a função inversa de 𝑓
será 𝑦 = 𝑓−1(𝑥) = −√𝑥 − 1 , que é um número negativo ou nulo.
Vamos fazer as composições:
(𝑓 ∘ 𝑓−1)(𝑥) = 𝑓(𝑓−1(𝑥)) = 𝑓(−√𝑥 − 1) = (−√𝑥 − 1)
2
+ 1 = (𝑥 − 1) + 1 = 𝑥.
(𝑓−1
∘ 𝑓)(𝑥) = 𝑓−1
(𝑓(𝑥)) = 𝑓−1(𝑥2
+ 1) = −√(𝑥2 + 1) − 1 = −√𝑥2 = −|𝑥| = −(−𝑥) = 𝑥, pois
como 𝑥 ∈ 𝐷𝑜𝑚(𝑓) = (−∞, 0] , então 𝑥 ≤ 0 e, portanto, |𝑥| = −𝑥.
Esboçando os gráficos de 𝑦 = 𝑓(𝑥) e 𝑦 = 𝑓−1
(𝑥) no mesmo sistema de coordenadas:
_____________________________________________________________________________________
Exercício 8: Seja 𝑓(𝑥) = 𝑥3
− 3𝑥 ,para −2 ≤ 𝑥 ≤ 2.
a) Explique por que a função 𝑓, cujo gráfico está na
figura ao lado, não tem inversa em seu domínio.
b) Subdivida o domínio em três intervalos adjacentes
sobre cada um dos quais a função 𝑓 tem uma inversa.
RESOLUÇÃO:
a) A função 𝑓, do gráfico dado, não tem inversa em seu
domínio, pois não satisfaz o Teste da Reta Horizontal, não é
um a um.
-------------------------------------------------------------------------------------------------------------------------------------------

b) Podemos subdividir o domínio em três intervalos adjacentes sobre cada um dos quais a função 𝑓
tem uma inversa. Esses intervalos são: [−2, −1], [−1, 1], [1, 2].
Esses intervalos foram escolhidos, pois em cada um deles a função é um a um, satisfaz
Teste da Reta Horizontal.
𝑓: [−2, −1] ⟶ [−2, 2]
𝑓: [−1, 1] ⟶ [−2, 2] 𝑓: [1, 2] ⟶ [−2, 2]
_____________________________________________________________________________________
Exercício 9: Dê o domínio das funções a seguir e esboce os seus respectivos gráficos. Essas funções
definem parte de uma curva já estudada. Elas são invertíveis?
a) 𝑓(𝑥) = −√16 − 𝑥2 b) 𝑔(𝑥) = −√4 − 𝑥 − 1
RESOLUÇÃO:
a) Seja 𝑓(𝑥) = −√16 − 𝑥2
Para que a raiz quadrada √16 − 𝑥2 possa ser calculada é preciso que 16 − 𝑥2
≥ 0. Mas,
16 − 𝑥2
≥ 0 ⟺ 𝑥2
≤ 16 ⟺ √𝑥2 ≤ √16 ⟺ |𝑥| ≤ 4 ⟺ −4 ≤ 𝑥 ≤ 4

Portanto, 𝐷𝑜𝑚(𝑓) = [−4, 4].
Para saber qual a curva que deu origem a esta função, vamos fazer alguns cálculos.
Considere a equação 𝑦 = −√16 − 𝑥2. Então,
𝑦 = −√16 − 𝑥2 ⟹ 𝑦2
= (−√16 − 𝑥2)
2
⟺ 𝑦2
= 16 − 𝑥2
⟺ 𝑥2
+ 𝑦2
= 16
Esta é a equação de um círculo de centro 𝐶(0,0)e raio 𝑟 = 4.
Como em 𝑓(𝑥) = −√16 − 𝑥2, 𝑦 ≤ 0, então o gráfico desta função
é o semicírculo, que está nos 3º. e 4º.quadrantes e mais os pontos
𝐴(−4, 0) e 𝐵(4, 0) sobre o eixo 𝑥 :
Esta função não é invertível, pois não é “um-a-um”.
É fácil ver graficamente que retas horizontais, como por exemplo,
𝑦 = −1, 𝑦 = −3 cortam a curva em dois pontos.
b) Seja 𝑔(𝑥) = −√4 − 𝑥 − 1
Para que a raiz quadrada √4 − 𝑥 possa ser calculada é preciso que 4 − 𝑥 ≥ 0 ⟺ 𝑥 ≤ 4.
Consideremos 𝑦 = −√4 − 𝑥 − 1 e vamos fazer algumas contas:
𝑦 = −√4 − 𝑥 − 1 ⟹ (𝑦 + 1)2
= (−√4 − 𝑥)
2
⟺ (𝑦 + 1)2
= 4 − 𝑥 ⟺ 𝑥 − 4 = −(𝑦 + 1)2
Esta é a equação canônica de uma
parábola de vértice no ponto 𝑉(4, −1),
concavidade voltada para esquerda e
tem como eixo de simetria a reta 𝑦 = −1.

Observação: a equação na forma (𝑥 − ℎ) = 𝑎(𝑦 − 𝑘)2
mostra que o coeficiente 𝑎 = −1 < 0, por isso a
parábola possui concavidade voltada para a esquerda.
Observe que,
𝑦 = −√4 − 𝑥 − 1 ⟺ 𝑦 + 1 = −√4 − 𝑥 ≤ 0 ⟺ 𝑦 + 1 ≤ 0 𝑦 ≤ −1
Portanto a função 𝑔(𝑥) = −√4 − 𝑥 − 1 é tal que, 𝑥 ≤ 4 e 𝑦 ≤ −1.
O seu gráfico é o ramo da parábola que está abaixo do eixo de simetria.
Veja ao lado.
O ponto (0, −3) é um ponto do gráfico dessa função,
como podemos verificar:
𝑔(0) = −√4 − 0 − 1 = −√4 − 1 = −2 − 1 = −3
Esta função é invertível, pois é “um-a-um”.
É fácil ver graficamente que retas horizontais, cortam a curva em no máximo um ponto.
_____________________________________________________________________________________
Exercício 10: Seja 𝑓(𝑥) =
𝑥3
𝑥2+4
uma função invertível.
a) Encontre 𝑥 se 𝑓−1(𝑥) = 3 b) Ache o valor de 𝑓−1(1) .
RESOLUÇÃO:
a) Sabemos que 𝑓−1(𝑥) = 3 ⟺ 𝑓(3) = 𝑥.
Assim, 𝑥 = 𝑓(3) =
33
32+4
=
27
9+4
=
27
13
.
-------------------------------------------------------------------------------------------------------------------------------------------
b) Suponha 𝑓−1(1) = 𝑥.
Sabemos que 𝑓−1(1) = 𝑥 ⟺ 𝑓(𝑥) = 1.
Mas, 𝑓(𝑥) = 1 ⟺
𝑥3
𝑥2+4
= 1 ⟺ 𝑥3
= 𝑥2
+ 4 ⟺ 𝑥3
− 𝑥2
− 4 = 0.
Como 𝑓 é uma função invertível então 𝑓 é uma função um-a-um e, portanto, existe um único valor de 𝑥,
tal que 𝑓(𝑥) = 1.
Pelo que afirmamos acima, existirá uma única raiz real para o polinômio 𝑝(𝑥) = 𝑥3
− 𝑥2
− 4 .
Começamos buscando as possíveis raízes inteiras desse polinômio, que estão entre os divisores do termo
independente −4, e são: −1, +1, −2, +2, −4, 4.
Testando esses valores, verificamos que 𝑝(2) = 23
− 22
− 4 = 8 − 4 − 4 = 0 . Assim, 𝑥 = 2 é raiz do
polinômio 𝑝(𝑥) e será, portanto, o único valor de 𝑥, tal que 𝑓(𝑥) = 1.

Logo, 𝑓−1(1) = 2.
Ainda não aprendemos em Pré-Cálculo como construir o
gráfico dessa função, mas em Cálculo I será possível construí-
lo, ele está desenhado ao lado.
-------------------------------------------------------------------------------------------------------------------------------------------
Exercício 11:
A figura ao lado apresenta o gráfico do polinômio
𝑝(𝑥) = 3𝑥4
− 4𝑥3
− 12𝑥2
+ 5 , restrito a um intervalo
𝐼 ⊂ ℝ.
a) Diga qual é o domínio dessa função. Responda na
forma de intervalo.
b) Esta função é monótona? Justifique sua resposta!
c) Marque no eixo 𝑥 os intervalos onde essa função é
decrescente. Diga quais são esses intervalos.
d) A função é monótona no intervalo [−1, 2]?
Justifique sua resposta.
e) Marque no eixo 𝑥 os intervalos onde essa função é
crescente. Diga quais são esses intervalos.
f) Diga qual é a imagem dessa função. Responda na forma de intervalo.
RESOLUÇÃO:
(a) Observando o gráfico vemos que 𝐷𝑜𝑚(𝑓) = [−2, 3].
(b) Essa função não é monótona, pois, por exemplo, ela é
decrescente no intervalo [−2, −1] e é crescente no intervalo
[−1, 0].
(c) Essa função é decrescente nos intervalos: [−2, −1], [0, 2].

(d) Essa função não é monótona no intervalo [−1, 2], pois, ela é crescente no intervalo [−1, 0] e é
decrescente no intervalo [0, 2].
(e) Essa função é crescente nos intervalos: [−1, 0], [2, 3].
(f) Observando o gráfico vemos
que.
𝐼𝑚(𝑓) = [𝑓(2), 𝑓(−2)] = [−27, 37]
____________________________________________________________________________
Exercício 12:
Desenhe, caso exista, o gráfico de uma função 𝑔 que satisfaz (simultaneamente) as seguintes
condições:
a) O domínio de 𝑔 é 𝐷 = [−3, −1] ∪ [1, 3]
b) A função 𝑔 é decrescente em [−3, −1].
c) A função 𝑔 é decrescente em [1, 3].
d) A função 𝑔 é não é decrescente em 𝐷 = [−3, −1] ∪ [1, 3].
RESOLUÇÃO:
b) Essa função é decrescente no intervalo
[−3, −1].
c) A função g é decrescente em [1, 3].
d) A função g é não é decrescente em 𝐷 =
[−3, −1] ∪ [1, 3]. De fato, temos por exemplo,
que;
−2 < 2 e 𝑓(−2) = 2 < 6 = 𝑓(2)
____________________________________________________________________________

Exercício 13:
a) Usando a definição de função decrescente, mostre que a função ℎ(𝑥) =
1
𝑥
é decrescente no intervalo
(0, +∞) .
b) Usando a definição de função decrescente, mostre que a função ℎ(𝑥) =
1
𝑥
(−∞, 0).
c) A função ℎ(𝑥) =
1
𝑥
é decrescente no seu domínio, que é (−∞, 0) ∪ (0, ∞)? Justifique sua resposta!
RESOLUÇÃO:
a) De fato:
Sejam 𝑥1, 𝑥2 ∈ 𝐴 = (0, ∞), com 𝑥1 < 𝑥2.
Assim, 0 < 𝑥1 < 𝑥2 ⟹ 0 <
1
𝑥2
<
1
𝑥1
⟹ ℎ(𝑥2) < ℎ(𝑥1)
Mostramos então que, ∀ 𝑥1, 𝑥2 ∈ 𝐴 , 𝑥1 < 𝑥2 ⟹ ℎ(𝑥2) < ℎ(𝑥1).
Ou, escrita de outra forma, ∀ 𝑥1, 𝑥2 ∈ 𝐴 , 𝑥1 < 𝑥2 ⟹ ℎ(𝑥1) > ℎ(𝑥2).
Portanto, concluímos que a função ℎ(𝑥) =
1
𝑥
é decrescente no intervalo 𝐴 = (0, ∞).
-------------------------------------------------------------------------------------------------------------------------------------------
b) Sejam 𝑥1, 𝑥2 ∈ 𝐵 = (−∞, 0), com 𝑥1 < 𝑥2.
Assim,
𝑥1 < 𝑥2 , 𝑥1 < 0, 𝑥2 < 0 ⟹
𝑥1
𝑥2
> 1 , 𝑥1 < 0 ⟹
1
𝑥2
<
1
𝑥1
< 0 ⟹ ℎ(𝑥2) < ℎ(𝑥1)
Mostramos então que, ∀ 𝑥1, 𝑥2 ∈ 𝐵 , 𝑥1 < 𝑥2 ⟹ ℎ(𝑥2) < ℎ(𝑥1).
Ou, escrita de outra forma, ∀ 𝑥1, 𝑥2 ∈ 𝐵 , 𝑥1 < 𝑥2 ⟹ ℎ(𝑥1) > ℎ(𝑥2).
Portanto, concluímos que a função ℎ(𝑥) =
1
𝑥
é decrescente no intervalo 𝐵 = (−∞, 0).
-------------------------------------------------------------------------------------------------------------------------------------------
c) Observe que −2 < 0 < 2 ⟹
1
−2
< 0 <
1
2
Portanto, a função ℎ(𝑥) =
1
𝑥
não é decrescente no seu
domínio, que é (−∞, 0) ∪ (0, ∞).
Para ilustrar, apresentamos ao lado o gráfico da função
citada.
_____________________________________________________________________________________

Exercício 14:
Usando a definição de função decrescente, mostre que a função 𝑓(𝑥) = 𝑥2
𝐴 = (−∞, 0].
RESOLUÇÃO:
De fato:
Sejam 𝑥1, 𝑥2 ∈ 𝐴 = (−∞, 0], com 𝑥1 < 𝑥2.
Assim, 𝑥1 < 𝑥2 ≤ 0, donde 𝑥1 < 0 e 𝑥1 − 𝑥2 < 0 . Como 𝑥1 < 0 e 𝑥2 ≤ 0 então 𝑥1 + 𝑥2 < 0 .
Sendo o produto de dois números reais negativos, um número real positivo, segue que:
(𝑥1 + 𝑥2) (𝑥1 + 𝑥2) > 0 ⟹ (𝑥1)2
− (𝑥2)2
> 0 ⟹ (𝑥1)2
> (𝑥2)2
⟹ 𝑓(𝑥1) > 𝑓(𝑥2)
Mostramos então que, ∀ 𝑥1, 𝑥2 ∈ 𝐴 , 𝑥1 < 𝑥2 ⟹ 𝑓(𝑥1) > 𝑓(𝑥2).
Portanto, concluímos que a função 𝑓(𝑥) = 𝑥2
é decrescente no
intervalo 𝐴 = (−∞, 0].
Para ilustrar, apresentamos ao lado o gráfico da função citada.
__________________________________________________________________________________
Exercício 15:
Mostre que se 𝑦 = 𝑓(𝑥) é uma função crescente em um intervalo [𝑎, 𝑏] então 𝑦 = 𝑔(𝑥) = −𝑓(𝑥) é
uma função decrescente neste mesmo intervalo.
RESOLUÇÃO:
Se 𝑦 = 𝑓(𝑥) é uma função crescente em um intervalo [𝑎, 𝑏] então
∀ 𝑥1, 𝑥2 ∈ [𝑎, 𝑏], 𝑥1 < 𝑥2 ⟹ 𝑓(𝑥1) < 𝑓(𝑥2) ⟹ −𝑓(𝑥1) > −𝑓(𝑥2) ⟹ 𝑔(𝑥1) > 𝑔(𝑥2).
Provamos assim que, ∀ 𝑥1, 𝑥2 ∈ [𝑎, 𝑏], 𝑥1 < 𝑥2 ⟹ 𝑔(𝑥1) > 𝑔(𝑥2)
Logo, 𝑦 = 𝑔(𝑥) = −𝑓(𝑥)é uma função decrescente no intervalo [𝑎, 𝑏].
___________________________________________________________________________________
Exercício 16:
Esboce o gráfico da função: 𝑦 = 𝑓(𝑥) = {
−|𝑥 + 3| + 2 𝑠𝑒 𝑥 < −2
𝑥2
− 3 𝑠𝑒 − 2 ≤ 𝑥 ≤ 2
−|𝑥 − 3| + 2 𝑠𝑒 𝑥 > 2
a) Determine os intervalos onde 𝑓 é crescente, onde 𝑓 é decrescente.
b) Determine os intervalos onde 𝑓(𝑥) ≤ −2. Mostre no gráfico, a parte do gráfico que satisfaz essa
condição.
c) A função 𝑓 é invertível? Justifique sua resposta!
d) Se a sua resposta para o item c) foi não, escolha dois possíveis intervalos onde é possível inverter a
função 𝑓 . Justifique sua escolha.

RESOLUÇÃO:
O gráfico da função
𝑦 = 𝑓(𝑥) = {
−|𝑥 + 3| + 2 𝑠𝑒 𝑥 < −2
𝑥2
− 3 𝑠𝑒 − 2 ≤ 𝑥 ≤ 2
−|𝑥 − 3| + 2 𝑠𝑒 𝑥 > 2
O gráfico de 𝑦 = −|𝑥 + 3| + 2 pode ser
construído a partir das seguintes transformações em gráficos de funções:
𝑦 = |𝑥|
𝑟𝑒𝑓𝑙𝑒𝑥ã𝑜 𝑒𝑚
𝑡𝑜𝑟𝑛𝑜 𝑑𝑜
𝑒𝑖𝑥𝑜 𝑥
→ 𝑦 = −|𝑥| 𝑡𝑟𝑎𝑛𝑠𝑙𝑎çã𝑜 ℎ𝑜𝑟𝑖𝑧𝑜𝑛𝑡𝑎𝑙
𝑑𝑒 3 𝑢𝑛𝑖𝑑𝑎𝑑𝑒𝑠
𝑝𝑎𝑟𝑎 𝑒𝑠𝑞𝑢𝑒𝑟𝑑𝑎
→ 𝑦 = −|𝑥 + 3| 𝑡𝑟𝑎𝑛𝑠𝑙𝑎çã𝑜 𝑣𝑒𝑟𝑡𝑖𝑐𝑎𝑙
𝑝𝑎𝑟𝑎 𝑐𝑖𝑚𝑎
→ 𝑦 = −|𝑥 + 3| + 2
Este gráfico será considerado no intervalo (−∞, −2).
O gráfico de 𝑦 = −|𝑥 − 3| + 2 pode ser construído a partir das seguintes transformações em gráficos de
funções:
𝑦 = |𝑥|
𝑟𝑒𝑓𝑙𝑒𝑥ã𝑜 𝑒𝑚
𝑡𝑜𝑟𝑛𝑜 𝑑𝑜
𝑒𝑖𝑥𝑜 𝑥
→ 𝑦 = −|𝑥| 𝑡𝑟𝑎𝑛𝑠𝑙𝑎çã𝑜 ℎ𝑜𝑟𝑖𝑧𝑜𝑛𝑡𝑎𝑙
𝑝𝑎𝑟𝑎 𝑑𝑖𝑟𝑒𝑖𝑡𝑎
→ 𝑦 = −|𝑥 − 3| 𝑡𝑟𝑎𝑛𝑠𝑙𝑎çã𝑜 𝑣𝑒𝑟𝑡𝑖𝑐𝑎𝑙
𝑝𝑎𝑟𝑎 𝑐𝑖𝑚𝑎
→ 𝑦 = −|𝑥 − 3| + 2
Este gráfico será considerado no intervalo (2, ∞).
O gráfico de 𝑦 = 𝑥2
− 3 pode ser construído a partir das seguintes transformações em gráficos de
funções:
𝑦 = 𝑥2
𝑡𝑟𝑎𝑛𝑠𝑙𝑎çã𝑜 𝑣𝑒𝑟𝑡𝑖𝑐𝑎𝑙
𝑝𝑎𝑟𝑎 𝑏𝑎𝑖𝑥𝑜
→ 𝑦 = 𝑥2
− 3
Este gráfico será considerado no intervalo [−2, 2].
a) Determine os intervalos onde 𝑓 é crescente, onde 𝑓 decrescente.
𝑓 é crescente nos intervalos: (−∞, −3] , [0, 3]
(parte em vermelho no gráfico ao lado).

𝑓.é decrescente nos intervalos: [−3, 0], [3, ∞)
(parte em vermelho no gráfico ao lado).
-------------------------------------------------------------------------------------------------------------------------------------------
b) Determine os intervalos onde 𝑓(𝑥) ≤ −2. Mostre no gráfico, a parte do gráfico que satisfaz essa
condição.
Pelo gráfico, observamos que temos que considerar as três expressões que fazem parte da definição da
função 𝑓(𝑥).
1) 𝑦 = −|𝑥 + 3| + 2 ≤ −2 para 𝑥 < −2.
−|𝑥 + 3| + 2 ≤ −2 ⟺ −|𝑥 + 3| ≤ −4 ⟺ |𝑥 + 3| ≥ 4 ⟺
𝑥 + 3 ≤ −4 ou 𝑥 + 3 ≥ 4 ⟺ 𝑥 ≤ −7 ou 𝑥 ≥ 1.
Como 𝑥 < −2, então 𝑦 = −|𝑥 + 3| + 2 ≤ −2 para 𝑥 ≤ −7.
2) 𝑦 = 𝑥2
− 3 ≤ −2 para −2 ≤ 𝑥 ≤ 2.
𝑥2
− 3 ≤ −2 ⟺ 𝑥2
− 1 ≤ 0 ⟺ −1 ≤ 𝑥 ≤ 1.
Como −2 ≤ 𝑥 ≤ 2 , então 𝑦 = 𝑥2
− 3 ≤ −2 para −1 ≤ 𝑥 ≤ 1.
3) 𝑦 = −|𝑥 − 3| + 2 ≤ −2 para 𝑥 > 2.
−|𝑥 − 3| + 2 ≤ −2 ⟺ −|𝑥 − 3| ≤ −4 ⟺ |𝑥 − 3| ≥ 4 ⟺
𝑥 − 3 ≤ −4 ou 𝑥 − 3 ≥ 4 ⟺ 𝑥 ≤ −1 ou 𝑥 ≥ 7.
Como 𝑥 > 2, então 𝑦 = −|𝑥 − 3| + 2 ≤ −2, para 𝑥 ≥ 7.
Concluímos que 𝑓(𝑥) ≤ −2 em: (−∞, −7] ∪ [−1, 1] ∪ [7, ∞) (projeção no eixo 𝑥 da parte em verde no
gráfico acima)
-------------------------------------------------------------------------------------------------------------------------------------------

c) A função f é invertível? Justifique sua
resposta!
Não, a função não é invertível. Essa função não é
um-a-um, não é “aprovada” no Teste da Reta
Horizontal.
Do gráfico observamos que;
𝑓(−3) = 2 = 𝑓(3), 𝑓(−5) = 0 = 𝑓(5).
d) Se a sua resposta para o item c) foi não, escolha dois possíveis intervalos onde é possível inverter a
função 𝑓. Justifique sua escolha.
Podemos escolher, por exemplo, os seguintes intervalos:
1) Intervalo escolhido (−∞, −3]. Justificativa: considerando a parte verde do gráfico abaixo, temos o
gráfico de uma função crescente. A projeção no eixo 𝑥 desta parte do gráfico é o intervalo (−∞, −3].
Dizemos, portanto, que no intervalo (−∞, −3] do domínio, a função 𝑓 é crescente, logo é um-a-um,
sendo assim, invertível.
2) Intervalo escolhido [−3, 0]. Justificativa: considerando a parte vermelha do gráfico abaixo, temos o
gráfico de uma função decrescente. A projeção no eixo 𝑥 desta parte do gráfico é o intervalo [−3, 0].
Dizemos, portanto, que no intervalo [−3, 0] do domínio, a função 𝑓 é decrescente, logo é um-a-um, sendo
assim, invertível.
3) Intervalo escolhido [0, 3]. Justificativa: considerando a parte azul do gráfico abaixo, temos o gráfico
de uma função crescente. A projeção no eixo 𝑥 desta parte do gráfico é o intervalo [0, 3]. Dizemos,
portanto, que no intervalo [0, 3] do domínio, a função 𝑓 é crescente, logo é um-a-um, sendo assim,
invertível.
4) Intervalo escolhido [3, ∞). Justificativa: considerando a parte preta do gráfico abaixo, temos o gráfico
de uma função decrescente. A projeção no eixo 𝑥 desta parte do gráfico é o intervalo [3, ∞). Dizemos,
portanto, que no intervalo [3, ∞) do domínio, a função 𝑓 é decrescente, logo é um-a-um, sendo assim,
invertível.

PC_2020-2_EP07_Paridade. Inversa. Crescimento_GABARITO.pdf

Mais conteúdo relacionado

Semelhante a PC_2020-2_EP07_Paridade. Inversa. Crescimento_GABARITO.pdf

Último

PC_2020-2_EP07_Paridade. Inversa. Crescimento_GABARITO.pdf