Fisica

2. Tipo de trajetória
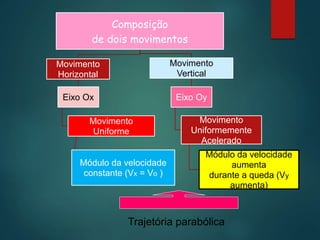
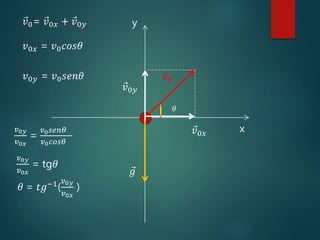
O tipo de trajetória de uma partícula sujeita a uma força
resultante constante depende da orientação relativa da
velocidade inicial e da força resultante.
Se a velocidade inicial ( 𝑣0) e a força resultante ( 𝐹𝑅) tiverem
a mesma direção, a trajetória é retilínea.
Se a velocidade inicial ( 𝑣0) e a força resultante ( 𝐹𝑅) tiverem
direções diferentes, a trajetória é curvilínea.

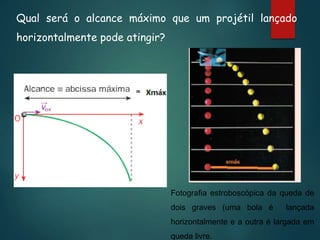
3. Uma bola em queda livre (sujeita apenas a uma única
força – o peso ou força gravítica) cai verticalmente com
movimento retilíneo uniformemente acelerado.
𝑃

4. MOVIMENTO RETILÍNEO
UNIFORMEMENTE VARIADO
Neste movimento a aceleração é constante e igual à
aceleração tangencial, com aceleração normal nula.
Lei das posições: Lei das velocidades:
𝑥 = 𝑥0 + 𝑣0t +
1
2
𝑎𝑡2
𝑟 = 𝑟0 + 𝑣0t +
1
2
𝑎𝑡2
𝑣 = 𝑣0 + 𝑎𝑡
𝑣 = 𝑣0 + 𝑎𝑡

5. Projéteis
 O termo projétil aplica-se quer a uma bala disparada por
um canhão quer a outro qualquer objeto lançado ao ar
(pedra, bola, etc).
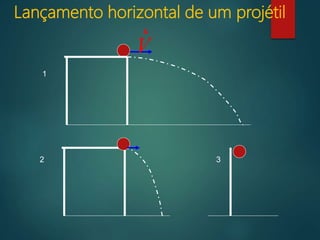
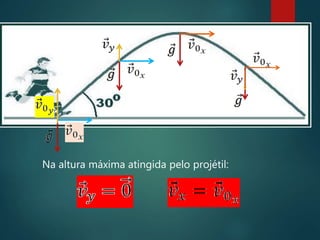
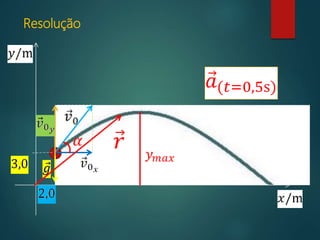
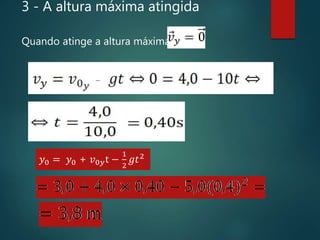
 O movimento de um projétil é um caso particular de um
movimento sob ação de uma força constante, quando é
desprezável a resistência do ar.
 O lançamento de um projétil pode ser vertical, horizontal
ou oblíquo.

6. Lançamento horizontal de um projétil
V
r
1
2 3

8. Composição
de dois movimentos
Movimento
Horizontal
Eixo Ox
Movimento
Uniforme
Módulo da velocidade
constante (Vx = Vo )
Movimento
Vertical
Eixo Oy
Movimento
Uniformemente
Acelerado
Módulo da velocidade
aumenta
durante a queda (Vy
aumenta)
Trajetória parabólica

9. Decomposição do vetor
velocidade, ao longo do
movimento.
y

10. Equações das leis do movimento
x0 = 0
y0 = h
vox = v0
voy = 0
h
Condições iniciais do movimento:
O movimento
decorre sempre
no plano definido
pela aceleração e
pela velocidade
inicial.

11. EQUAÇÕES DAS LEIS DO MOVIMENTO
Na vertical (Eixo Oy)
0
0
0;
0
;2 2
0
( )
1 1
( )
2 2
y
v a g
y
a g y h
v t v at v gt
y t y at y h gt
  
  
    
    
Na horizontal (Eixo Ox)
0 00;
0 0( ) xx v v
x t x vt x v t 
   

12. Como se pode determinar o tempo de
queda?
O tempo de queda ou tempo de voo é determinado pelo
movimento vertical.
O instante de queda corresponde à chegada ao solo
(y = 0), de acordo com o sistema de eixos escolhido, logo:
2 2 2
queda queda queda
queda
1 1 2
0
2 2
2
ou seja, o tempo de queda é:
h
h gt h gt t
g
h
t
g
     


14. Qual será o alcance máximo que um projétil lançado
horizontalmente pode atingir?
Fotografia estroboscópica da queda de
dois graves (uma bola é lançada
horizontalmente e a outra é largada em
queda livre.

15. O alcance depende do valor da velocidade de
lançamento e da altura inicial.

16. LANÇAMENTO OBLÍQUO DE PROJÉTEIS
No lançamento oblíquo, um projétil tem, na direção horizontal, um
movimento retilíneo uniforme e, na direção vertical, um movimento
retilíneo uniformemente variado.

17. y
x
𝑔
𝑣0
𝑣0𝑥
𝑣0𝑦
𝑣0= 𝑣0𝑥 + 𝑣0𝑦
𝑣0𝑥 = 𝑣0 𝑐𝑜𝑠𝜃
𝜃
𝑣0𝑦 = 𝑣0 𝑠𝑒𝑛𝜃
𝑣0𝑦
𝑣0𝑥
=
𝑣0 𝑠𝑒𝑛𝜃
𝑣0 𝑐𝑜𝑠𝜃
𝑣0𝑦
𝑣0𝑥
= tg𝜃
𝜃 = 𝑡𝑔−1(
𝑣0𝑦
𝑣0𝑥
)

18. Na altura máxima atingida pelo projétil:

19. LEIS DAS POSIÇÕES
𝑥0 = 𝑥0 + 𝑣0𝑥t
𝑦0 = 𝑦0 + 𝑣0𝑦t −
1
2
𝑔𝑡2
𝑟𝑦 = 𝑟0𝑦 + 𝑣0𝑦t +
1
2
𝑎𝑡2
𝑟𝑥 = 𝑟0𝑥 + 𝑣0𝑥t
𝑟 = x 𝑒 𝑥 + y 𝑒 𝑦

20. LEIS DAS VELOCIDADES
𝑣 𝑦 = 𝑣0𝑦 − 𝑔𝑡
𝑣 𝑥 =
𝑑𝑥
𝑑𝑡
𝑣 𝑦 =
𝑑𝑦
𝑑𝑡

21. RESOLVE O EXERCÍCIO
Um projétil é lançado de um ponto (2,0; 3,0) m com
velocidade inicial:
Seja
Determine:
1 - o ângulo de lançamento;
2 - o vetor posição no instante t= 0,2 s ;
3 - a altura máxima atingida;
4 - a aceleração no instante t = 0,5 s .

22. Resolução

23. 1 - o ângulo de lançamento;

24. 2 - O vetor de posição no instante 0,2 s ;
2
2,0 3,0 0,2
3,0 4,0 0,2 5 0,2
x
y
  

    
𝑦0 = 𝑦0 + 𝑣0𝑦t −
1
2
𝑔𝑡2

25. 3 - A altura máxima atingida
Quando atinge a altura máxima,
𝑦0 = 𝑦0 + 𝑣0𝑦t −
1
2
𝑔𝑡2

26. 4 - A aceleração no instante 0,5 s.
A aceleração é constante, logo