Incorporar apresentação
Transferir como PDF, PPTX


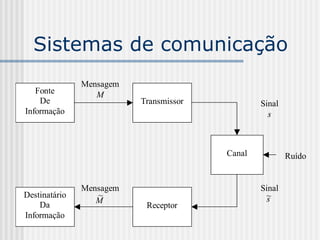



















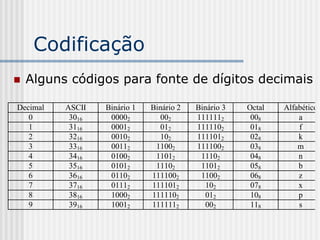


















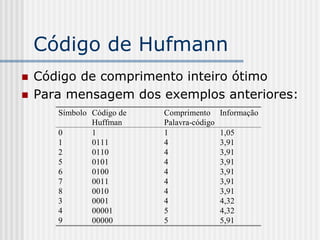





























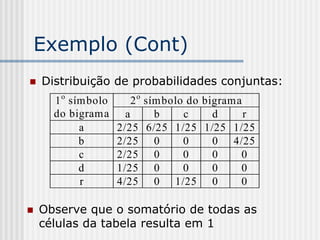


























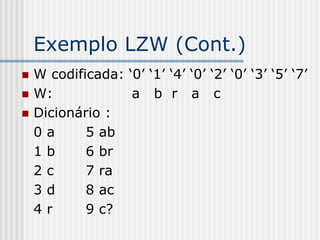














































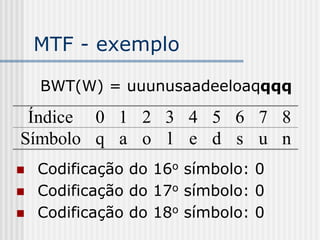















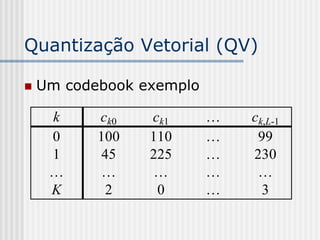








1) A teoria da informação estuda as comunicações e é baseada na concepção formal de "informação" e na capacidade de transmissão de informação pelos canais de comunicação. 2) A compressão de dados é uma aplicação da teoria da informação que reduz a quantidade de dados em uma mensagem preservando a informação. 3) A informação é uma medida da incerteza ou surpresa relacionada a um evento e é relativa ao processo de comunicação.








































































































































































