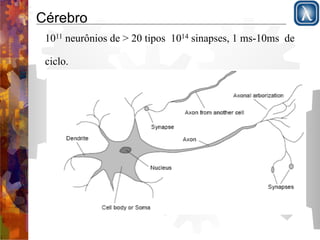
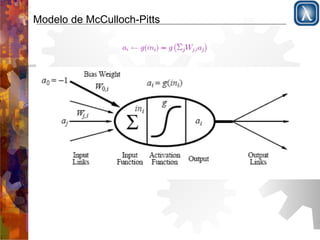
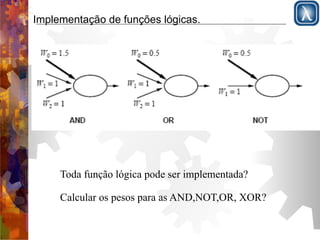
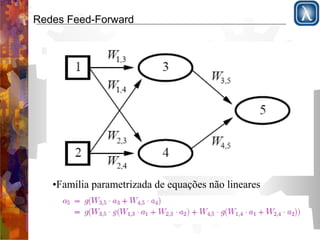
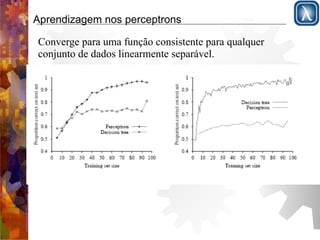
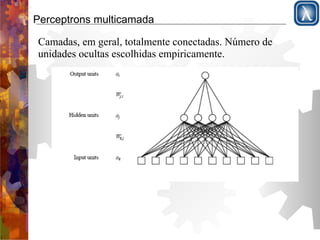
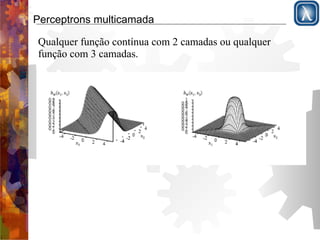
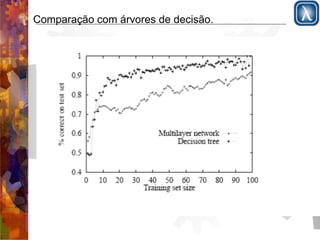
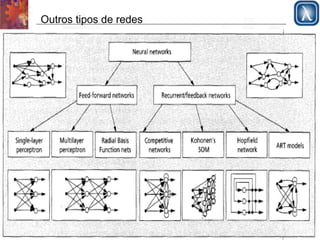
O documento discute redes neurais, começando com a estrutura do cérebro e modelo de McCulloch-Pitts. Apresenta perceptrons de camada simples e multicamadas, explicando que perceptrons de camada simples são insuficientemente expressivos, ao contrário de redes multicamadas que podem representar qualquer função contínua. Descreve o algoritmo de retropropagação para treinamento de redes multicamadas.


![Função de ativação
a) Função limiar
b) Função sigmóide 1/(1-e-x)
Mudando o bias muda a posição do limiar W[0,1]](https://image.slidesharecdn.com/cursoiamecatronica-parte11-redesneurais-141017065951-conversion-gate01/85/Inteligencia-Artificial-Parte-6-IA-5-320.jpg)

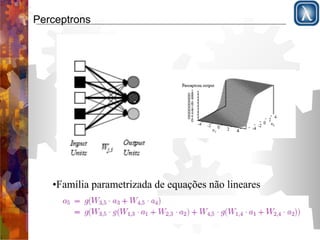





![Inteligência Artificial Parte 6 [IA]](https://image.slidesharecdn.com/cursoiamecatronica-parte11-redesneurais-141017065951-conversion-gate01/85/Inteligencia-Artificial-Parte-6-IA-21-320.jpg)