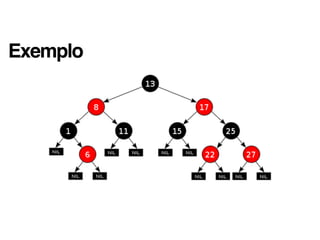
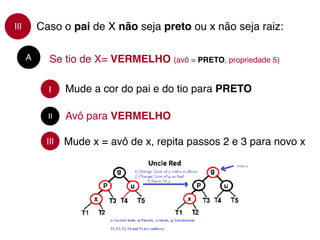
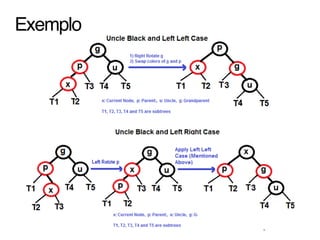
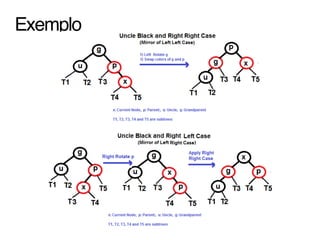
Uma árvore rubro-negra é uma árvore binária de busca auto-balanceada onde cada nó possui uma cor (vermelha ou preta) e as propriedades de balanceamento são mantidas durante inserções e remoções, garantindo operações de busca, inserção e remoção em O(log n).

1. RUBRO
NEGRA

2. O que é uma árvore rubro-negra?
É uma Árvore Binária de Busca (ABB) com auto-balanceamento,
III
I
IV
II
Cada nó tem tem uma cor: Preta ou Vermelha
O nó raíz é sempre preto
Não há dois nós vermelhos adjacentes
Todas as folhas são pretas
V Cada caminho raiz -> nó NULL mesma
quantidade de nós pretos

3. Exemplo

4. Por que usar?
Operações em uma ABB - busca,
min, máx, insert, delete -> O(h);
na qual h altura da árvore
Árvore desbalanceada -) O(n)
Se inserir e apagar = O(lgn) =>
O(logn) para as outras operações
A altura de um ARN (RBT) é
sempre O(logn)
(n - números de nós)

5. RUBRO-NEGRA
VS
AVL
As AVLs são mais
balanceadas
Menor quantidade de
rotações ao inserir/
apagar nó.
Muitas operações de
inserir/apagar -> ARN

6. Como é feita a inserção?
São utilizadas duas ferramentas após a inserção, para rebalancear.
I
II
recolorir
rotacionar

7. Algoritmo
Dependendo da cor do nó tio, dois casos:
I
II
Se o tio foi vermelho -> recolorir
Se o tio for preto -> rotação e/ou recolorir
Novo nó X
Inserção ABB e o novo nó = vermelho
Se X for raiz, troque a cor para preta (a altura +1)
I
II

8. I
II
Mude a cor do pai e do tio para PRETO
Avô para VERMELHO
III Caso o pai de X não seja preto ou x não seja raiz:
A Se tio de X= VERMELHO (avô = PRETO, propriedade 5)
Mude x = avô de x, repita passos 2 e 3 para novo xIII

9. I
II
caso esquerda-esquerda - p é filho da esquerda de a e
x é filho a esquerda de p
caso esquerda-direita - p é filho da esquerda de
g e x é filho da direita de p
III Caso o pai de X não seja preto ou x não seja raiz:
B Se o tio for preto 4 configurações possiveis para x, pai (p) e
avô (a) de X - similar com AVL:
caso direita-direita - caso espelhado iIII
IV caso direita-esquerda - caso espelhado ii

10. Exemplo

11. Exemplo

12. Como é feita a remoção?
Assim como a inserção:
I
II
recolorir
rebalancear

13. Passos
I
Delete do AVL - no final temos um nó com apenas um
filho ou uma folha, para nós internos - chamadas
recursivas do Delete.
Seja : v - nó a ser deletado;
u - filho que vai tomar o lugar de v
Lembre-se: u é NULL quando v é folha e NULL = PRETO
II Caso Simples:
Quando u ou v é VERMELHO
Fazemos:
u = PRETO

14. Passos
III Quando u e v PRETOS
A u como PRETO duplo
Tarefa: converter o DUPLO PRETO para PRETO
SIMPLES.
Lembrando: se v folha, então u é NULL (NULL =
PRETO) - então a remoção de uma folha PRETA
causa duplo preto

15. Passos
B Enquanto o nó atual for DUPLO PRETO ou não é a raiz,
fazendo o nó irmão s.
“Se s é PRETO e pelo menos um dos sobrinhos for VERMELHO,
ROTAÇÃO. O sobrinho VERMELHO será chamado de r. São quatro
casos dependendo da posição de r e s.”
III
I
II
Caso ESQUERDO - ESQUERDO: s é filho a esquerda e r é filho a
esquerda de s ou ambos os filhos de s VERMELHOS.
Caso ESQUERDA - DIREITA: s é filho a esquerda e r é filho a
direita.
Caso DIREITA-DIREITA: s é filho a direita e r é filho a direita
ou ambos os filhos de s são VERMELHOS.
IV Caso ESQUERDA-DIREITA: s é filho a direita e r é filho a
esquerda

16. Passos
Caso o pai = VERMELHO -> faça o nó PRETO (VERMELHO +
DUPLO PRETO = PRETO SIMPLES )
Converte para o caso de 3 irmãos PRETO, pode ser dividido em
dois subcasos?
“Se o irmão é PRETO ambos os seus filhos PRETOS -> RECOLORIR e
refaça para o PAI se o pai for PRETO.”
“Se o irmão é VERMELHO: ROTACIONE para mover o irmão mais
velho para cima, RECOLORIR o novo PAI e IRMÃO.”
I
II
caso ESQUERDA (s é filho a esquerda) - ROTACIONA a DIREITA
o pai p.
caso DIREITA (s é filho a direita ) - ROTACIONA a ESQUERDA o
pai p.

17. Cristiano Oliveira
Marcos Levi
Mariana Ogawa
Rafael Parente
Renata Theóphilo