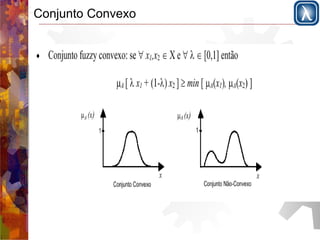
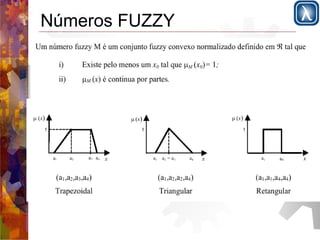
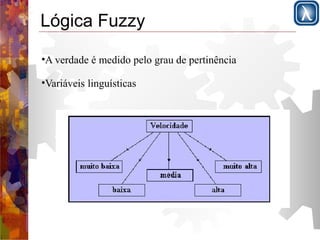
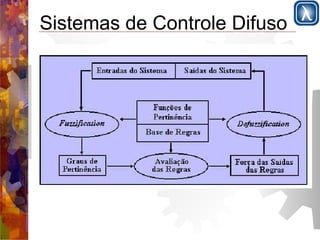
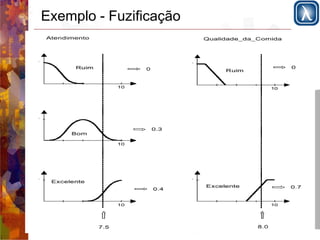
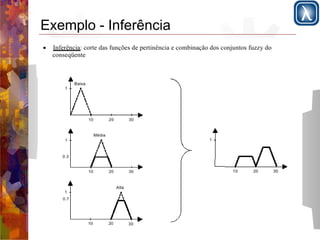
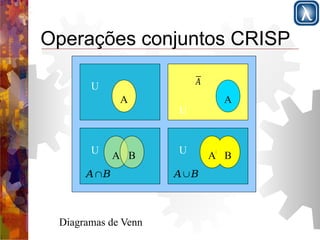
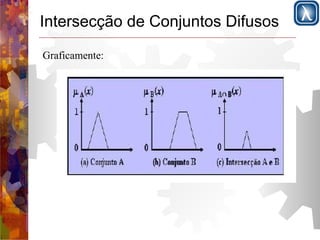
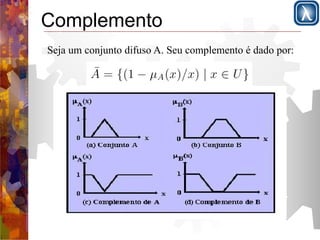
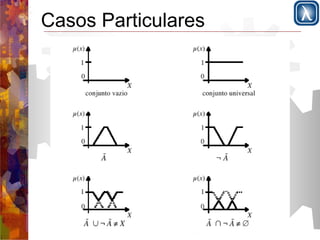
Este documento apresenta os conceitos fundamentais de sistemas difusos (fuzzy) em 3 frases: Apresenta a lógica clássica versus lógica difusa e define conjuntos difusos utilizando funções de pertinência entre 0 e 1; Descreve operações básicas com conjuntos difusos como união, interseção e complemento; Introduz a lógica difusa com variáveis linguísticas, partições difusas e regras de produção para sistemas de controle difuso.

1. Sistemas Difusos
(Fuzzy)
Ronaldo F. Ramos, Dr.
ronaldo@cefet-ce.br

2. Roteiro
 Lógica clássica x Lógica Difusa
 Sistemas Difusos
 Aplicações em Controle
 Inferência Difusa
 Arquitetura de Sistemas Difusos

3. Lógica Clássica
Começou com Aristóteles. (384 – 322 A.C)
Sejam os enunciados abaixo:
Premissas:
- Todo Homem é Mortal
- Sócrates é um Homem
Conclusão:
- Sócrates é Mortal
Formalmente
∀xHxMx
Hs
Ms
O que se pode afirmar sobre a semântica das afirmações
acima?
- Cada assertiva pode assumir valores V ou F
- Nenhuma assertiva pode ser parcialmente V ou F.
- Nenhuma assertiva pode ser ao mesmo tempo V e F.
No mundo real as coisas acontecem sempre desta forma?

4. Conjuntos Clássicos
Mortais (M)
Humanos
Sócrates
Sócrate∈sHumano⊂sMortais
Diz-se que um elemento pertence ou não pertence a um
conjunto.

5. Função de Pertinência
Dada uma função f(e,C)=[0..1] onde
e= e1,e2 ...en representa os elementos do conjunto
C= Representa o conjunto clássico relacionado aos
elementos e.
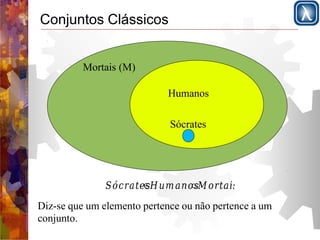
Então para conjuntos clássicos:
f(e,C)=
0 ssee ∉C
1 ssee ∈C
Para conjuntos difusos:
f(e,C)= [0..1]

6. Conjuntos Difusos
Seja D um conjunto definido como:
D= {e,f e,C  } onde:
e : elementos do conjunto C
f(e,C) : grau de pertinência de e em C
C é considerado como o conjunto de suporte do conjunto
difuso D
Chamamos: μC = f(e,C) a função de pertinência com
domínio U (universo) e imagem contida no intervalo [0..1]
ou seja: μC: U [0..1]

7. Conjuntos Difusos
Exemplo1. Conjunto dos números próximos de 1
P = {...(-2,0)(-1,1/3)(0,2/3)(1,1)(2,2/3)(3,1/3)(4,0)...}
Onde:
suporte(P) = {...-2,-1,0,1,2,3,4...}
μP =
0 sse e≤−2 ou e≥4
e+2
3 sse −2<e≤1
4−e
3 sse 1<e<4

8. Conjuntos Difusos
Representação Gráfica D = {(e,μD(e))}
-4 -3 -2 -1 0 1 2 3 4 5 6
1,2
1
0,8
0,6
0,4
0,2
0
Números Próximos de 1
fuzzy
Crisp
Representação Formal:.
D={de/e∣e∈U}

9. Funções de Pertinência
Triangular TrapTerzioaindgaullar
Retangular Universo Contínuo
9

10. Operações conjuntos CRISP
A
U
A
A
U
U A B U
A∩B
A B
A∪B
Diagramas de Venn

11. Operações com Conjuntos Difusos
Sejam os conjuntos difusos:
A={a x/x∣x∈U}
B={bx/x∣x∈U}
A união A U B é dada por:
A∪B={max{a x,b x}/x∣x∈U}
Onde:
a∪b=max {a x,bx}

12. União de Conjuntos Difusos
Exemplo.
Sejam os conjuntos difusos:
ALTO ={ (0/1.5), (0,2/1.55), (0,5/1.6), (0,8/1.65), (1/1.7 })
BAIXO = { (1/1.5), (0,8/1.55), (0,5/1.6), (0,2/1.65), (0/1.7)}
Então:
Co-Norma T
ALTO U BAIXO = ALTO v BAIXO
{ (1/1.5), (0,8/1.55), (0,5/1.6), (0,8/1.65), (1/1.7)}

13. União de Conjuntos Difusos
Representação Gráfica da União de conjuntos Difusos

14. Intersecção (Norma T)
Sejam os conjuntos difusos:
A={a x/x∣x∈U}
B={bx/x∣x∈U}
A intersecção entre A e B é dada por:
A∩B={min{a x,bx}/x∣x∈U}
Onde:
a∩b=min{a x,bx}

15. Intersecção
Exemplo.
Sejam os conjuntos difusos:
ALTO ={ (0/1.5), (0,2/1.55), (0,5/1.6), (0,8/1.65), (1/1.7 })
BAIXO = { (1/1.5), (0,8/1.55), (0,5/1.6), (0,2/1.65), (0/1.7)}
Então:
ALTO ∩ BAIXO ≡ ALTO ∧ BAIXO
= { (0/1.5), (0,2/1.55), (0,5/1.6), (0,2/1.65), (0/1.7)}

16. Intersecção de Conjuntos Difusos
Graficamente:

17. Complemento
Seja um conjunto difuso A. Seu complemento é dado por:

18. Casos Particulares

19. Mais definições
Seja A um conjunto difuso: A={a x/x∣x∈U}
O Conjunto Suporte de A é definido como:
suporteA={x∈X∣a x0}
O Núcleo (core) de A é definido como:
coreA={x∈X∣a x=1}
O ponto de crossover é definido como:
x∈X∣a x=0,5

20. Relações

21. Corte

22. Altura de um Conjunto Difuso
 Altura de A:
h(A)=Altura
normal: se h(A) = 1
subnormal:s e h(A) 1

23. Conjunto Convexo

24. Números FUZZY

25. Teoria dos Conjuntos Difuso
 Área similar a Teoria dos Conjuntos da Matemática:
 Fique à Vontade para estudar ............

26. Lógica Fuzzy
•A verdade é medido pelo grau de pertinência
•Variáveis linguísticas

27. Lógica Difusa

28. Lógica Difusa
Partição difusa da Variável lingüística Temperatura:

29. Lógica Difusa
Regras de Produção
Regras de Controle
Ordem das Regras não é Importante!

30. Sistemas de Controle Difuso

31. Fuzificação

32. Base de Regras

33. Avaliação das Regras - Inferência

34. Defuzificação - Centróide
Centróide ou centro de Massa
Média dos Máximos
First of Maxima
Primeiro Máximo
Outros ...

35. Defuzificação - Centróide

36. Defuzificação – Médias dos Máximos

37. Exemplo

38. Exemplo - Fuzificação

39. Exemplo - Fuzificação

40. Exemplo - Inferência

41. Exemplo Defuzificação

42. Exemplo 2
Ver Aplicações Fuzzy.ppt