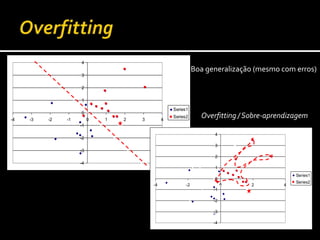
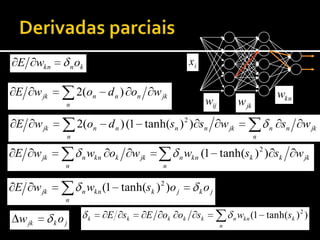
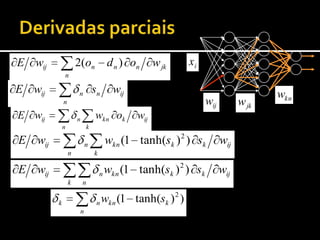
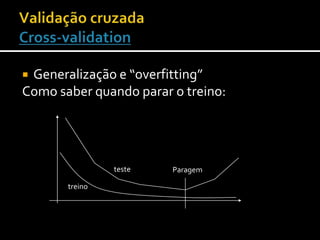
1) O documento discute técnicas de aprendizagem automática supervisionada como regressão, classificação e redes neurais artificiais. 2) A retropropagação é descrita como um método para treinar redes neurais através da propagação de erros e atualização dos pesos para minimizar o erro. 3) Várias técnicas são discutidas para acelerar a convergência da retropropagação incluindo taxas de aprendizagem adaptativas e momento.

1. AprendizagemAutomática Mestrado em Engenharia Informática

2. Sumário Aprendizagem Supervisionada 18-10-2010 Aprendizagem Automática / Machine Learning 2

4. Reformulação Se assumirmos que a função é linear Será que a partir de um conjunto de pontos (x, f(x)) conseguimos saber w1 e w2? (i.e., qual a “regra” usada para gerar os pontos) Encontrar os pesos para minimizar o erro:

7. Aproximação Por exemplo, se soubermos que: Se , e fizermos: O erro diminui (se o passo (α) for suf. pequeno) Demonstração

8. Classificação Queremos uma função com parâmetros wij, que dê os seguintes resultados: Que tipo de função é mais adequado?

9. Algo como: Mas a derivada é sempre zero ou infinita (?) Classificação Perceptrão [McCullogh & Pitts 43] Regra Delta (delta-rule)

10. É necessária uma aproximação contínua: Funções para classificação b - Termo de polarização (bias). Funciona como uma fasquia regulável. ou …

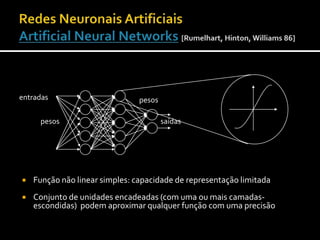
11. Função não linear simples: capacidade de representação limitada Conjunto de unidades encadeadas (com uma ou mais camadas-escondidas) podem aproximar qualquer função com uma precisão arbitrária (desde que … ) Redes Neuronais ArtificiaisArtificial Neural Networks[Rumelhart, Hinton, Williams 86] entradas pesos pesos saídas

12. Capacidade de divisão do espaço Funções para classificação

13. Codificação / Compressão Redes Neuronais ArtificiaisArtificial Neural Networks

14. Projecção num espaço de maiores dimensões de modo a tornar as classes separáveis (na prática, combinando de modos diferentes as features de entrada de modo a criar características que definem bem as classes) Redes Neuronais ArtificiaisArtificial Neural Networks

15. Os métodos analíticos de classificação / regressão têm desvantagens quando os dados têm ruído e/ou muitos exemplos. São também sensíveis em relação a aproximações numéricas. As ANN são: Robustas em relação ao ruído e aproximações Baseadas num modelo (muito simplificado) do funcionamento dos neurónios Podem ser treinadas incrementalmente Condensam a informação de grandes conjuntos de dados num conjunto comparativamente pequeno de pesos Redes Neuronais Artificiais

16. Apresentar cada exemplo (xi,di) Calcular a resposta da rede para xi: f(xi) Propagar para trás o erro (construindo a derivada do erro em relação a cada peso) Ao fim de cada época: actualizar os pesos RetropropagaçãoBackpropagation

17. Vantagens das funções de activação apresentadas: As derivadas num ponto calculam-se à custa do valor nesse ponto (possibilidade de implementação paralela) Retropropagação

18. Cálculo da derivada é simples com base no valor da avaliação Menos cálculos (do que outras funções semelhantes): Menos erros de aproximação Mais rápido Redes Neuronais Artificiais

19. Overfitting Boa generalização (mesmo com erros) Overfitting / Sobre-aprendizagem

20. Generalização e “overfitting” Como saber quando parar o treino: Validação cruzadaCross-validation teste Paragem treino

22. Treino, Teste, Validação

23. Conjuntos pequenos (k-foldvalidation/leaven-off)Dividir dados em k subconjuntos Em cada uma de k experiências usar um dos conjuntos para validação Calcular nº médio de iterações (n) para minimizar erro de validação Treinar com todos os dados n épocas Validação

24. Termo de momento (momentum) Duas vezes na mesma direcção, acelera, Em direcções contrárias, trava (ou não é usado). Valor típico: 0.8 Aceleração de Backprop

25. A mesma taxa de aprendizagem para todos os pesos faz com que se mova com a mesma “velocidade” em todas as direcções Solução: taxas de aprendizagem diferentes para cada peso Aceleração de Backprop

26. ALR (AdaptiveLearning Rates): Aceleração de Backprop

27. Técnica dos passos-adaptativos AdaptiveLearning Rates F. M. Silva and L. B. Almeida, "Acceleration Techniques for the Backpropagation Algorithm", in L. B. Almeida and C. J. Wellekens (eds.), Neural Networks, Springer-Verlag, 1990. Aceleração de ANN

28. Dicas de implementação: Deve ser fácil mudar a função (e a sua derivada), a tanh() é, normalmente, melhor Deve ser possível ter 2 ou 3 camadas Deve ser fácil mudar a taxa de aprendizagem Experimentar primeiro com um caso muito simples Use sempre uma taxa de aprendizagem baixa para começar (1E-7) Vá aumentando a taxa até verificar que de uma época para a seguinte há alteração da média do erro Diminua a taxa de aprendizagem ao longo do treino Use valores desejados abaixo do limite da função (e.g. -0.9 e 0.9, para a tanh) Redes Neuronais Artificiais 27 AA/ML, Luís Nunes, DCTI/ISCTE

29. [Rumelhart, Hinton, Williams 86] D.E.Rumelhart, G.E.Hinton and R.J.Williams, "Learning internal representa-tions by error propagation", In David E. Rumelhart and James A. McClelland, volume 1. The MIT Press, 1986. [Rumelhart, Widrow, Lehr] David E. Rumelhart, Bernard Widrow, Michael A. Lehr, The basic ideas in neural networks, Communications of the ACM archive, Volume 37 , Issue 3 (March 1994) table of contents, pp 87 – 92, 1994, ISSN:0001-0782 , Publisher ACM Press New York, NY, USA F. M. Silva and L. B. Almeida, "Acceleration Techniques for the Backpropagation Algorithm", in L. B. Almeida and C. J. Wellekens (eds.), Neural Networks, Springer-Verlag, 1990. OutrasReferências: [McCullough & Pitts 43] W. S. McCullough, W. Pitts, LogicalCalculusoftheideasimmanentinnervousactivity, Contemp. Math, 113, pp. 189-219 [Minsky & Papert 69] Minsky M L and Papert S A 1969 Perceptrons (Cambridge, MA: MIT Press) Referências-base 28 AA/ML, Luís Nunes, DCTI/ISCTE

30. Sumário Aprendizagem Supervisionada 18-10-2010 Aprendizagem Automática / Machine Learning 29

31. Avaliação e erro

32. Derivadas parciais

33. Derivadas parciais

34. Derivadas parciais

35. Derivadas parciais

36. Actualização (batch) … ou, para evitar que seja um valor muito grande (overflow):

37. Actualização (online)