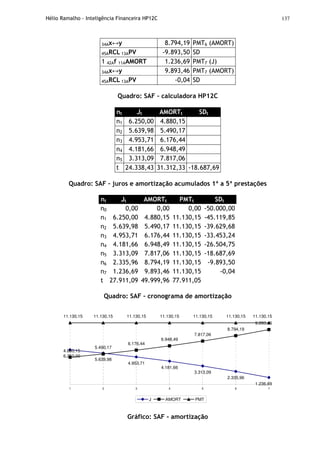
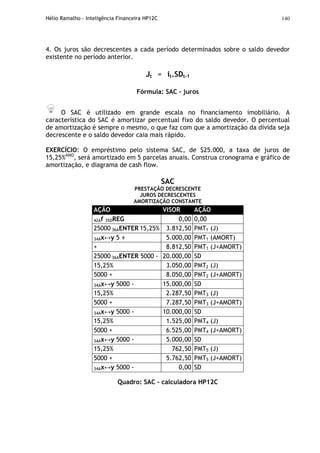
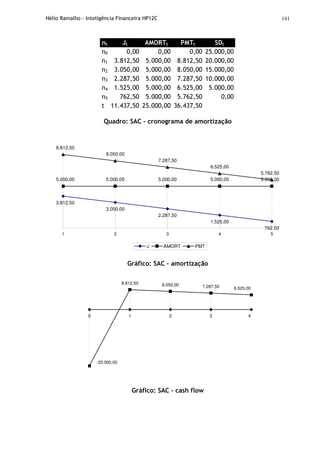
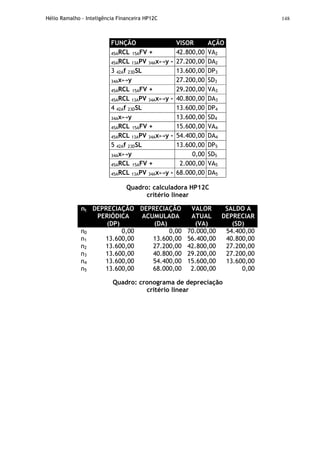
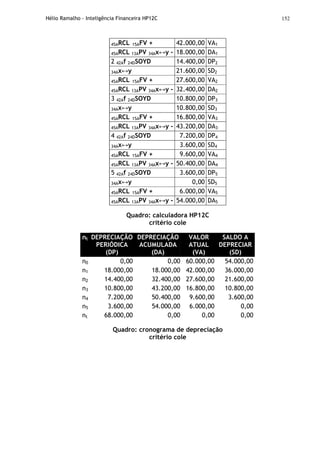
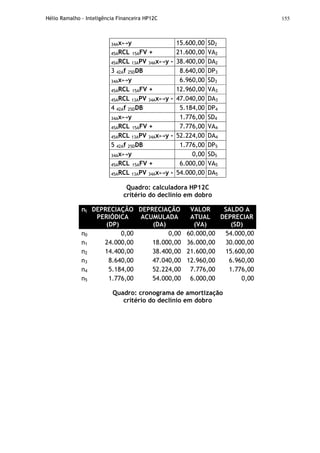
O documento apresenta uma introdução à calculadora financeira HP-12C, abordando seus fundamentos matemáticos e financeiros, como fluxo de caixa, juros simples e compostos, análise financeira de projetos e amortização. Inclui também explicações sobre o funcionamento da máquina, com seus registradores, memórias e teclas, preparando o leitor para utilizar a HP-12C em cálculos e análises financeiras.















![Hélio Ramalho - Inteligência Financeira HP12C 18
As empresas que necessitam de recursos por prazos maiores podem recorrer a essa
modalidade de financiamento, se as suas previsões indicarem uma tendência de
queda nas taxas de juros.
A taxa de juros do hot money é linear. Apresentada na forma de taxa mensal ao dia
útil ou taxa over. A convenção do mercado é usar a taxa efetiva de um dia útil
multiplicada por 30 dias.
Geralmente, para valores elevados, a operação é contratada por um dia e, caso
necessário, renovada no dia seguinte. O procedimento evita os riscos para as
partes, em períodos de elevada oscilação das taxas de juros.
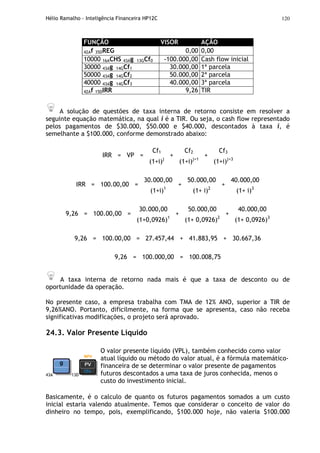
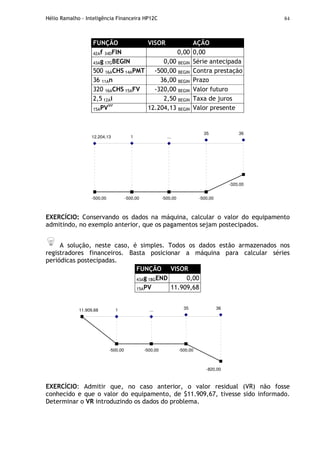
EXERCÍCIO: Com base nas taxas de hot money exibidas abaixo, calcule o montante
para um financiamento de $45.000, contratado por 5 dias corridos e 7 dias corridos.
CÁLCULO LINEAR DE FINANCIAMENTO – HOT MONEY
(1) (2) (3) (4) (5)
DIAS
CORRIDOS
DIAS
ÚTEIS
MENSAL LINEAR
DIÁRIA
EFETIVA
NO PERÍODO
1 1 6,978120% 0,232604% 0,232604%
2 2 6,986235% 0,232875% 0,465749%
3 3 6,994370% 0,233146% 0,699437%
4 4 7,002510% 0,233417% 0,933668%
5 5 7,010664% 0,233689% 1,168444%
6 5 5,842220% 0,194741% 1,168444%
7 5 5,007617% 0,166921% 1,168444%
A variação ( ) efetiva (5) foi calculada pela fórmula [((3)÷(1)].
A taxa diária (4) foi calculada pela fórmula ((5)÷(1)).
VF = VP.(1=i.n)
VF = {45.000,00[1+(0,07010664 x 5/30)]} = 45.525,80
VF = {45.000,00[1+(0,07010664 x 7/30)]} = 45.736,12
O montante ou valor futuro calculado para 5 ou 7 dias corridos é o mesmo, por
conter o mesmo número de dias úteis.
A taxa do hot money é diferente nos dois casos, mas a taxa efetiva no período
é a mesma.](https://image.slidesharecdn.com/helram-intelfin-130605192551-phpapp01/85/Helio-Ramalho-18-320.jpg)









![Hélio Ramalho - Inteligência Financeira HP12C 28
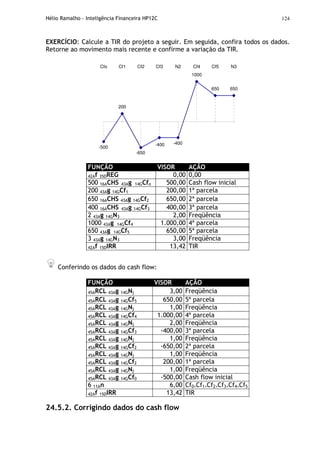
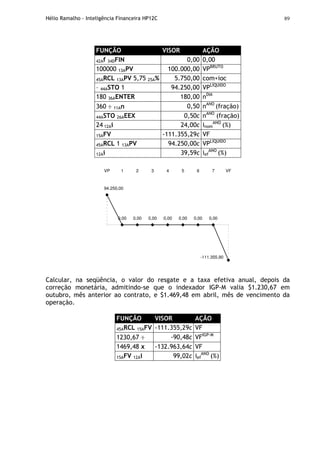
EXERCÍCIO: Com a calculadora desligada, vamos verificar se todos os flags do visor
estão funcionando corretamente.
TECLAS VISOR AÇÃO
X (segure)
41AON (solte) 0,00 Liga
X (solte) running Flags
-8,8,8,8,8,8,8,8,8,8
USER f g BEGIN GRAD D.MY C PRGM
Figura: Teste automático
7.2. Teste semi-automático
EXERCÍCIO: Com a calculadora desligada, pressione e mantenha pressionada a tecla
÷ e depois ligue a HP12C, pressionando a tecla 41AON. Solte a tecla 41AON e depois a
tecla ÷
TECLAS VISOR AÇÃO
÷ (segure)
41AON (solte) 0,00 Liga
÷ (solte) running Flags
-8,8,8,8,8,8,8,8,8,8
USER f g BEGIN GRAD D.MY C PRGM
Figura: Teste semi-automático
Para verificar todas as teclas da HP12C, nesta opção de teste é necessário
pressionar TODAS as teclas da máquina, da esquerda para a direita, de cima para
baixo.
Ou seja, é necessário pressionar todas as teclas, da tecla 11AN até a tecla ÷, depois
da tecla 34Ay↔x até a tecla x, da tecla 31AR/S até a tecla -, pressionando, na
passagem, a tecla 36AENTER e, por último, da tecla 41AON até a tecla [+], passando,
também, pela tecla 36AENTER.
Assim, a tecla 36AENTER deverá ser pressionada em duas passagens distintas. Por
isso, a função é grafada na FIGURA 1 como 36AENTER e 46AENTER.
De forma similar ao teste anterior, se o mecanismo da máquina estiver funcionando
corretamente, após pressionar todas as teclas na ordem descrita, o visor indicará o
número 12 no centro.
Se aparecer a expressão "Error 9" ou não aparecer nada, a calculadora está com
problemas. Recomendo você procurar suporte no site ou uma oficina de assistência
técnica autorizada pela fabricante.](https://image.slidesharecdn.com/helram-intelfin-130605192551-phpapp01/85/Helio-Ramalho-28-320.jpg)











![Hélio Ramalho - Inteligência Financeira HP12C 40
19.1. Cadeia de cálculos: sem parênteses e sinal de igual
A rapidez e a simplicidade dos cálculos quando se utiliza RPN são evidentes numa
cadeia de cálculos com mais de uma operação. A pilha de memória RPN, como verá
adiante, armazena resultados intermediários. A adição de percentagem e a raiz
cúbica são dois exemplos elementares de cadeias de cálculos.
EXERCÍCIO: Calcular 7x(12+3)
Inicie o cálculo dentro dos parênteses encontrando 12+3. Observe que não
precisa pressionar 36AENTER para salvar resultados intermediários. Sendo um
resultado calculado, esse é um saldo automático – sem utilizar parênteses.
FUNÇÃO VISOR AÇÃO
42Af 35DREG 0,00 0,00
12 36AENTER 3 + 15,00 Intermediário
7 x 105,00 7x(12+3)
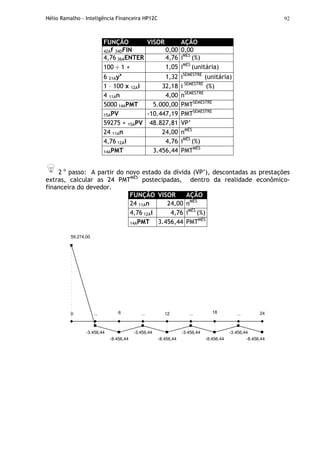
EXERCÍCIO: Calcular [(750x12)÷360]
FUNÇÃO VISOR AÇÃO
42Af 35DREG 0,00 0,00
750 36AENTER 12 x 360 ÷ 25,00 [(750x12)x360]
19.2. RPN: Pilha automática de memória
Como vimos, o armazenamento automático de resultados intermediários é a razão
pela qual o modo RPN facilmente processa cálculos complicados – sem utilizar
parênteses e o sinal de igual. A chave para o armazenamento automático é a pilha
automática de memória RPN.
A pilha de memória, área de trabalho para cálculos, consiste de até 4 posições de
armazenamento chamadas registradores, os quais são “empilhados” uns em cima
dos outros.
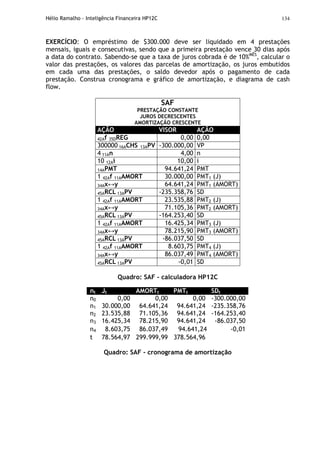
Esses registradores, rotulados como X, Y, Z e T, armazenam e manipulam 4
números correntes. O número “mais antigo” será o que estiver no registrador T
(topo da pilha). O número “recente” é o que estiver no visor.
T 0 Número “mais antigo”
Z 0
Y 0
X 0 Número “mais recente” - Visor
Figura: Modo RPN – Lógica Lukasiewics](https://image.slidesharecdn.com/helram-intelfin-130605192551-phpapp01/85/Helio-Ramalho-40-320.jpg)



![Hélio Ramalho - Inteligência Financeira HP12C 44
FUNÇÃO VISOR AÇÃO
42Af 35DREG 0,00 0,00
2 36AENTER 36AENTER 36AENTER 2,00 Constante
84000 84.000,00 Ano 0
x 168.000,00 Ano 1
x 336.000,00 Ano 2
x 672.000,00 Ano 3
0 1 2 3
84.000
168.000
672.000
336.000
O processo automático de levantar e deixar cair o conteúdo da pilha permite a
retenção de resultados intermediários sem retrabalho, e sem utilizar parênteses e
sinal de igual. Essa é uma vantagem da pilha RPN sobre a Lógica Algébrica.
19.7. Principais recursos da Lógica RPN
1. Nunca é preciso trabalhar com mais de dois números ao mesmo tempo.
2. A tecla 36AENTER separa dois números digitados em seqüência.
3. Pressionar uma tecla de operação executa o cálculo imediatamente.
4. Resultados intermediários aparecem quando são calculados, podendo ser
checado cada passo do cálculo.
5. Resultados intermediários são armazenados automaticamente.
Reaparecendo, quando solicitados, para novos cálculos. O último resultado
armazenado é o primeiro a reaparecer.
Podemos calcular na mesma ordem que faríamos com lápis e papel – de dentro para
fora dos parênteses.
EXERCÍCIO: Calcular [360÷(750x12)]
FUNÇÃO VISOR AÇÃO
42Af 35DREG 0,00 0,00
360 36AENTER 750 36AENTER 12 x ÷ 0,04 Produto](https://image.slidesharecdn.com/helram-intelfin-130605192551-phpapp01/85/Helio-Ramalho-44-320.jpg)
![Hélio Ramalho - Inteligência Financeira HP12C 45
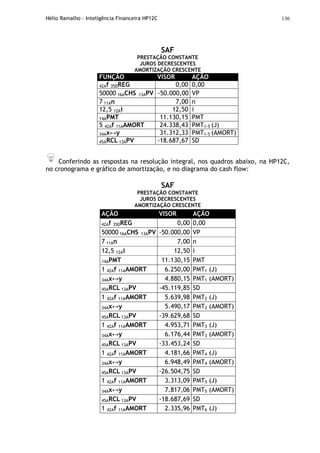
EXERCÍCIO: Calcular [((456-75)÷18,5).(68÷ 1,9)]
FUNÇÃO VISOR AÇÃO
42Af 35DREG 0,00 0,00
456 36AENTER 75 – 18,5 ÷ 68 36AENTER 1,9 ÷ x 737,07 Produto
EXERCÍCIO: Calcular √(5,4x0,8)÷(12,5-0,73
)
FUNÇÃO VISOR AÇÃO
42Af 35DREG 0,00 0,00
5,4 36AENTER 0,8 x 0,7 36AENTER
3 11Ay↔x 12,5 11Ay↔x - ÷ 43Ag 11G√x
0,6 Produto
EXERCÍCIO: Calcular [8,33x(4-5,2)÷(8,33-7,46)x0,32]
√ [4,3x(3,15-2,75)-(1,71x2,01)]
FUNÇÃO VISOR AÇÃO
42Af 35DREG 0,00 0,00
8,33 36AENTER 4 36AENTER 5,2 - x
8,33 36AENTER 7,46 – 0,32 x ÷
4,3 36AENTER 3,15 36AENTER 2,75 – x
1,71 36AENTER 2,01 x - ÷ 43Ag 11G√x
4,57 Produto
20. Operadores matemáticos
20.1. Soma, Multiplicação, Subtração e Divisão
O modo RPN exige a digitação dos valores para depois efetuar a operação
aritmética. A tecla 36AENTER separa números digitados e o operador matemático
completa o cálculo.
Não precisa utilizar 36AENTER antes de um operador.
Operador matemático é função assistente, na cor branca, acionada
diretamente.](https://image.slidesharecdn.com/helram-intelfin-130605192551-phpapp01/85/Helio-Ramalho-45-320.jpg)














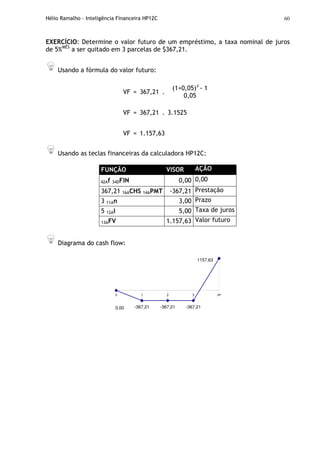

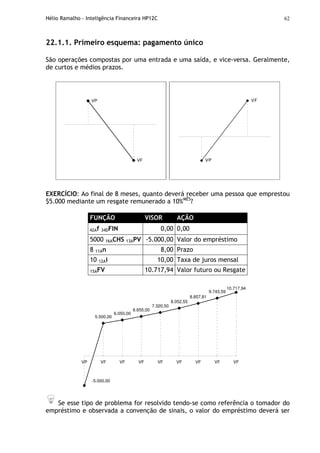

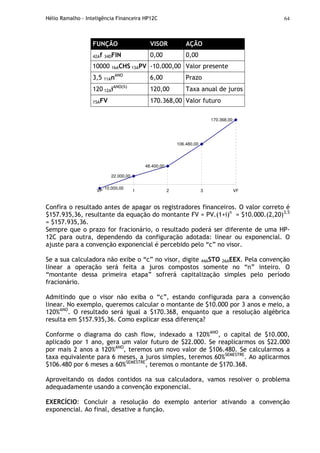


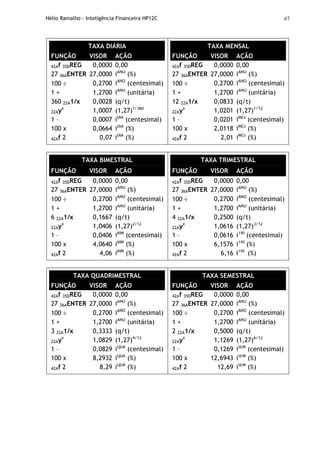

























![Hélio Ramalho - Inteligência Financeira HP12C 97
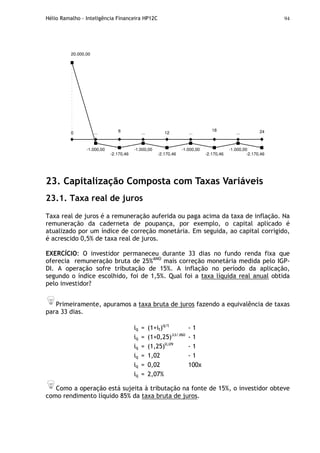
Mantida a premissa de constância ou igualdade das taxas de juros, a taxa
acumulada é calculada a partir da fórmula da taxa equivalente de juros. Se as
taxas forem diferentes, podemos deduzir que:
Utilizando a fórmula da taxa acumulada de juros:
iac = (1+i1)n
(1+i2)n
(1+i3)n
... (1+in)n
- 1
Fórmula: Taxa acumulada de juros
iac = (1+0,0453)1
(1+0,0356)1
(1+0,0562)1
(1+0,0485)1
- 1
iac = 1,1988 - 1
iac = 0,1988 100x
iac = 19,88%QUA
23.3. Taxa média de juros
A taxa média de juros é útil para atuar nos mercados de capitais e commodities,
bem como formular políticas empresariais de orçamentos e investimentos, com ou
sem subsídios de capital de terceiros.
EXERCÍCIO: Conhecida a taxa de 19,88%QUA
, qual é a taxa média mensal?
Usando a fórmula de equivalência da taxa quadrimestral para mensal de juros:
iq = (1+i)q/t
- 1
iq = (1+0,1988)1/4
- 1
iq = 0,0464 100x
iq = 4,64%MÊS
EXERCÍCIO: Como calcular a taxa média mensal de juros de três meses
consecutivos com as seguintes taxas: 8,5%, 10,5% e 11,02%?
im = [(1+i1)n
(1+i2)n
(1+i3)n
... (1+in)n
]1/n
- 1
Fórmula: Taxa média de juros
im = [(1+0,085)1
(1+0,105)1
(1+0,1102)1
]1/3
- 1
im = 1,1000 - 1
im = 0,1000 100x
im = 10,00%MÊS](https://image.slidesharecdn.com/helram-intelfin-130605192551-phpapp01/85/Helio-Ramalho-97-320.jpg)








![Hélio Ramalho - Inteligência Financeira HP12C 106
C = V = N - Dc = 6.000,00 – 504,00 = 5.496,00
A+B+C = V = N - Dc = 23.500,00 – 1.260,00 = 22.240,00
Usando a fórmula da taxa efetiva de juros, para encontrar a taxa efetiva
mensal de juros do desconto de cada duplicata:
A = ief =
VF
VP - X
1
21/30
- 1 =
8.000,00
7.776,00
30
21
-1 = 4,14%MÊS
A = ief =
VF
VP - X
1
42/30
- 1 =
9.500,00
8.968,00
30
42
-1 = 4,20%MÊS
A = ief =
VF
VP - X
1
63/30
- 1 =
6.000,00
5.496,00
30
63
-1 = 4,27%MÊS
Sofisticando a resposta, podemos indicar a taxa média efetiva de juros da
operação, usando a fórmula da taxa média de juros:
im = [(1+i1)n
(1+i2)n
(1+i3)n
... (1+in)n
]1/n
- 1
im = [(1+0,0414)1
(1+0,0420)1
(1+0,427)1
]1/3
- 1 = 4,20%
A taxa média efetiva da operação é igual à taxa efetiva de juros o prazo de 42
dias, que também é o prazo médio da operação.
24.3.1. Determinação da taxa de desconto
EXERCÍCIO: Qual a taxa de desconto para 30 dias, quando a taxa efetiva anual de
juros, objetivada pela instituição financeira, é de 30%ANO
.
Sempre que a questão envolver o cálculo do prazo ou da taxa DIÁRIA de juros,
na sua HP12C, pressione 42Af 4 para fixar 4 casas decimais e, ao final, pressione 42Af
2 para retornar 2 casas decimais.
Utilizando a fórmula de equivalência de taxas.
iq = (1+i)q/t
- 1 = (1+0,30)30/360
- 1 = 0,022104 = 2,2104%](https://image.slidesharecdn.com/helram-intelfin-130605192551-phpapp01/85/Helio-Ramalho-106-320.jpg)