Este documento apresenta os fundamentos da geometria espacial euclidiana. Introduz os conceitos de elementos primitivos do espaço como pontos, retas e planos, e os axiomas que regem as relações entre esses elementos. Explica propriedades básicas do espaço como separação por planos, ângulos e congruência, e apresenta noções iniciais sobre paralelismo e perpendicularismo entre retas e planos no espaço tridimensional.






![7
Introdu¸c˜ao
INTRODUC¸ ˜AO
Caras e caros alunas e alunos, neste livro apresentamos os fundamentos da geometria espacial
euclidiana, e pode ser visto como uma continua¸c˜ao do livro [7]. Na verdade, o que chamamos
“Fundamentos da Geometria Euclidiana” n˜ao deveria ser separado em geometria plana e
geometria espacial, pois ´e um s´o assunto, coeso. Esta separa¸c˜ao ´e apenas uma forma de
apresentar a geometria euclidiana de maneira mais did´atica e pr´atica.
Adotaremos neste texto todas as nomenclaturas, terminologias e nota¸c˜oes estabelecidas
em [7], em sua maioria tradicionais e utilizadas em quase todos os textos que tratam de
geometria euclidiana. Suporemos que todos vocˆes est˜ao familiarizados com os termos utili-zados
nesse livro. Em caso de d´uvidas, consultem-no.
Abaixo, como uma forma de refrescar a mem´oria, listamos as principais nota¸c˜oes que utili-zaremos.
Pontos serao ˜denotados por letras latinas maiusculas ´(A, B, etc.).
Retas serao ˜em geral denotadas por letras latinas minusculas ´(r, s, etc.). No caso
em que apresentarmos retas determinadas por dois pontos espec´ıficos usaremos uma
seta de duas pontas () sobre as letras que nomeiam os pontos. Por exemplo, a reta
determinada pelos pontos A e B sera ´denotada por
AB.
Para semirretas adotamos uma notac¸ao ˜analoga ´a `para retas, mas as demarcaremos
por uma seta com uma ponta (). Por exemplo, o s´ımbolo r denota a semirreta r;
e o s´ımbolo
AB denota a semirreta com origem no ponto A e passando pelo ponto B.
Segmentos de reta ser˜ao demarcados por uma barra cont´ınua sobre as letras que no-meiam
os pontos que determinam o mesmo. Por exemplo, o segmento de extremos A
e B ser´a denotado por AB. A medida de um segmento ser´a denotada pelos extremos
do mesmo, sem a barra. Por exemplo, a medida de AB ´e AB.
ˆAngulos ser˜ao denotados pelo s´ımbolo . Por exemplo, um ˆangulo chamado ser´a
denotado por ; e um ˆangulo determinado por trˆes pontos A, B, C, com origem
em B, ser´a denotado por ABC. A medida de um ˆangulo , por exemplo, ser´a
denotada por m().
Os nossos novos elementos, os planos, ser˜ao denotados, como manda a tradi¸c˜ao, por
letras gregas min´usculas (, , , etc.). N˜ao h´a perigo de confundir uma letra grega
que represente um plano com a mesma que denote um ˆangulos, pois a segunda sempre
vir´a acompanhada com o s´ımbolo .
Para facilitar a consulta de vocˆes listamos no apˆendice A os axiomas da geometria plana
euclidiana introduzidos em [7], e algumas defini¸c˜oes b´asicas.
5
Fundamentos de Geometria Espacial.indd 7 28/01/2013 11:09:23](https://image.slidesharecdn.com/fundamentosdegeometriaespacial-sergio-02-141028100838-conversion-gate01/85/Fundamentos-de-geometria_espacial-sergio-02-7-320.jpg)



![aula 1: O Espaço 11
AULA1: O ESPAC¸O
OBJETIVOS
Introduzir os conceitos elementos primitivos e de axiomas da Geometria Euclidiana no
espa¸co. Apresentar os axiomas de “incidˆencia” e algumas de suas consequˆencias.
1.1 Introdu¸c˜ao
Todos temos uma ideia bem intuitiva do conceito que denominamos “espa¸co”: ´e o ambi-ente
em que vivemos, onde podemos nos mover para os lados, para cima e para baixo,
o mundo “tridimensional”, ou seja, que possui trˆes dimens˜oes, uma a mais que o mundo
plano, bidimensional. Costumamos dizer que somos seres “tridimensionais” por vivermos
neste tal espa¸co. Pois bem, um conceito aparentemente t˜ao simples na verdade esconde uma
complexidade filos´ofica, f´ısica e matem´atica que n˜ao imaginamos1. Neste curso n˜ao vamos
discutir estas profundas quest˜oes, mas abordaremos este assunto da mesma maneira que se
faz quando estudamos a geometria plana do ponto de vista axiom´atico.
Figura 1.1
Nosso ponto de partida neste curso, como j´a o dissemos na Introdu¸c˜ao, ´e o texto [7], onde
apresentamos um modelo axiom´atico para a geometria plana euclidiana. Recomendamos a
todos os estudantes, portanto, que releiam este texto, principalmente as aulas um a trˆes.
Antes de come¸carmos, vamos abordar um problema pr´atico que se tem quando estudamos
geometria espacial: como representar visualmente as figuras tridimensionais. Desenhar fi-guras
planas ´e f´acil, pois as p´aginas de um livro, por exemplo, s˜ao boa representa¸c˜ao de um
plano. Desenhar figuras que vivem no espa¸co, por outro lado, representa um desafio, j´a que
os desenhos devem ser apresentados sobre a mesma folha de papel. Assim a imagina¸c˜ao dos
leitores ser´a muito mais exigida neste curso do que num curso de geometria plana. Vamos
mostrar alguns exemplos.
Para come¸car, representaremos um plano no espa¸co em geral como na figura 1.1 (na ver-dade,
uma “por¸c˜ao” de um plano – use a imagina¸c˜ao!). Usaremos, em geral, letras gregas
min´usculas para nomear estes objetos; no nosso exemplo denotamos o plano por .
1O leitor interessado poder´a estudar mais sobre isto no livro “Conceitos de espa¸co: a hist´oria das teorias do
espa¸co na f´ısica”, de Max Jammer, editado pela Editora Contraponto no Brasil.
Fundamentos de Geometria Espacial.indd 11 28/01/2013 11:09:25](https://image.slidesharecdn.com/fundamentosdegeometriaespacial-sergio-02-141028100838-conversion-gate01/85/Fundamentos-de-geometria_espacial-sergio-02-11-320.jpg)

![aula 1: O Espaço 13
1.2 Elementos primitivos e axiomas
Em [7] apresentamos os trˆes elementos primitivos da geometria plana: os pontos as retas e
o plano. Quando passamos para o espa¸co “aumentamos” uma “dimens˜ao geom´etrica”, isto
´e, passamos a ver um universo onde temos v´arios planos, todos essencialmente c´opias de
um mesmo “modelo”: o plano estudado num curso de geometria plana. Do ponto de vista
formal acrescentamos mais um elemento primitivo em nossa lista. Agora nossos elementos
primitivos ser˜ao os pontos, as retas, os planos (no plural, e n˜ao mais no singular!) e o
espa¸co. Mas aten¸c˜ao! Esta n˜ao ´e uma “nova geometria”. Separamos estes assuntos –
geometria plana e geometria espacial – por quest˜oes did´aticas, mas s˜ao todas partes de um
conjunto ´unico. Em particular, todos os resultados da geometria plana continuam v´alidos,
inclusive os axiomas.
Em [7] apresentamos um sistema axiom´atico da geometria plana dividido em seis grupos
(veja o apˆendice A):
Grupo I: axiomas de incidˆencia.
Grupo II: axiomas de m´etrica na reta e ordem na reta e no plano.
Grupo III: axiomas de medidas de ˆangulos.
Grupo IV: axiomas de congruˆencia de triˆangulos.
Grupo V: axioma das paralelas.
Grupo VI: axiomas sobre ´areas de figuras planas.
Para estudarmos a geometria no espa¸co precisaremos atualizar a lista de axiomas. Mas esta
opera¸c˜ao n˜ao ser´a muito traum´atica, pois a ´unica modifica¸c˜ao (na verdade uma extens˜ao) que
precisa ser feita ´e nos axiomas do grupo I, para abarcar as inter-rela¸c˜oes entre os elementos
primitivos que agora incluem planos e o espa¸co.
Os trˆes axiomas do grupo I listados em [7] permanecem como est˜ao, apenas trocando-se a
palavra plano por espa¸co.
Axioma I.1. Por dois pontos distintos do espa¸co passa uma e somente uma reta.
Observa¸c˜ao 1.1. Neste texto adotamos a mesma linguagem geom´etrica estabelecida em [7].
Por exemplo, no axioma acima usamos o termo “passar” no sentido de que dados dois pontos
distintos do espa¸co ent˜ao existe apenas uma reta que os cont´em.
Axioma I.2. Toda reta do espa¸co possui pelo menos dois pontos distintos.
Axioma I.3. O espa¸co cont´em pelo menos trˆes pontos distintos que n˜ao pertencem a
uma mesma reta.
Em seguida precisamos estabelecer condi¸c˜oes an´alogas `as dadas nos axiomas I.1 e I.2 para
planos – isto ´e as condi¸c˜oes de determina¸c˜ao de um plano por pontos, e o fato de planos
serem conjuntos n˜ao vazios do espa¸co. Primeiro observe o que nossa experiˆencia nos traz:
se vocˆe toma um banco com trˆes pernas e o coloca no ch˜ao, ver´a que ele n˜ao claudica (veja
figura 1.4).
Fundamentos de Geometria Espacial.indd 13 28/01/2013 11:09:25](https://image.slidesharecdn.com/fundamentosdegeometriaespacial-sergio-02-141028100838-conversion-gate01/85/Fundamentos-de-geometria_espacial-sergio-02-13-320.jpg)







![AULA2: MAIS PROPRIEDADES DO ESPAC¸O
OBJETIVOS
Apresentar os outros axiomas da Geometria Euclidiana no espa¸co. Analisar, com cuidado,
as seguintes propriedades: separa¸c˜ao do espa¸co em semiespa¸cos, congruˆencias no espa¸co, e
paralelismo de retas no espa¸co.
Aula 2 – Mais propriedades do espaço 21
2.1 Introdu¸c˜ao
Na aula anterior apresentamos o nosso novo elemento primitivo, o espa¸co, e os axiomas
que regem as inter-rela¸c˜oes entre pontos, retas, planos e o espa¸co, chamados axiomas de
incidˆencia. Estes s˜ao, essencialmente, os ´unicos axiomas que precisam ser modificados em
rela¸c˜ao a um sistema axiom´atico para a geometria plana. Os outros, como j´a o dissemos,
permanecem v´alidos. Nesta aula estudaremos os axiomas dos outros grupos e veremos
algumas consequˆencias.
2.2 Separa¸c˜ao do espa¸co: semiespa¸cos
Vamos come¸car estabelecendo um axioma “curioso”, que sintetiza o que afirmamos na in-trodu
¸c˜ao acima:
Axioma E.1. Todos os axiomas dos grupos II, III, IV e V, apresentados em [7], s˜ao
v´alidos na geometria espacial, salvo algumas adapta¸c˜oes.
Queremos dizer com este axioma que todas as afirma¸c˜oes sobre propriedades da geometria
plana s˜ao v´alidas no espa¸co, com as devidas adapta¸c˜oes. Vamos ent˜ao “passar os olhos” nos
axiomas apresentados em [7], chamando a aten¸c˜ao para os pontos mais complicados.
Os axiomas II.1 a II.5 de [7] tratam de medida de segmentos, da ordem de pontos numa reta
e de semirretas. Estas propriedades s˜ao transcritas automaticamente para o espa¸co, como
se pode ver facilmente.
Problema 2.1. Reveja os axiomas II.1 a II.5 de [7] e tente visualiz´a-los no espa¸co.
O axioma II.6, que trata da separa¸c˜ao de um plano em semiplanos por retas, ser´a analisado
com mais detalhes. Vamos reescrever seu enunciado, dentro de nosso novo contexto.
Figura 2.1: – Axioma II.6
Fundamentos de Geometria Espacial.indd 21 28/01/2013 11:09:28](https://image.slidesharecdn.com/fundamentosdegeometriaespacial-sergio-02-141028100838-conversion-gate01/85/Fundamentos-de-geometria_espacial-sergio-02-21-320.jpg)
![Axioma II.6. Toda reta l em um plano determina exatamente dois subconjuntos
l e ˜l de , denominados semiplanos de em rela¸c˜ao a l, satisfazendo as seguintes
propriedades:
(a) todos os pontos de est˜ao contidos em l ˜l;
(b) l ˜l = l;
(c) dois pontos A e B de n˜ao pertencentes a l est˜ao num mesmo semiplano de em
rela¸c˜ao a l se e somente se AB l = ;
(d) dois pontos A e B n˜ao pertencentes a l est˜ao em semiplanos distintos de em
rela¸c˜ao a l se e somente se AB l .
Problema 2.2. Compare este enunciado do axioma II.6 com o enunciado do mesmo em [7]
e aponte as diferen¸cas. Aproveite a oportunidade e reescreva os enunciados dos outros
axiomas apresentados em [7], colocando-os no novo contexto.
Na figura 2.1 representamos dois planos e no espa¸co. Eles s˜ao cortados pelas retas l
e s, respectivamente, que dividem cada um em dois semiplanos. No caso do plano , por
exemplo, os pontos A e B est˜ao do mesmo lado1 em rela¸c˜ao a l, e os pontos B e C est˜ao em
lados opostos.
Problema 2.3. Na figura 2.1 identifique todos os pontos representados, dizendo de que lado
est˜ao em cada plano e , em rela¸c˜ao `as retas l e s, respectivamente.
Situa¸c˜ao an´aloga `a descrita no axioma II.6 vale no espa¸co, isto ´e, um plano determina no
espa¸co dois conjuntos com propriedades exatamente equivalentes `as propriedades descritas
neste axioma. No entanto, esta propriedade n˜ao precisa ser estabelecida como um axioma,
mas ´e consequˆencia do axioma II.6, como enunciamos no teorema seguinte.
22 Fundamentos de geometria espacial
Figura 2.2: – Separa¸c˜ao do Espa¸co
Teorema 2.1 (Separa¸c˜ao do espa¸co). Todo plano do espa¸co determina exatamente dois
subconjuntos n˜ao vazios E e E
do espa¸co, denominados semiespa¸cos em rela¸c˜ao a ,
satisfazendo as seguintes propriedades:
(a) todos os pontos do espa¸co est˜ao contidos em E E
;
1Lembramos que os lados de um plano em rela¸c˜ao a uma reta l s˜ao os conjuntos l e ˜ l, na
nota¸c˜ao do axioma II.6, onde o s´ımbolo “” – vale a pena recordar – significa diferen¸ca de conjuntos.
Fundamentos de Geometria Espacial.indd 22 28/01/2013 11:09:28](https://image.slidesharecdn.com/fundamentosdegeometriaespacial-sergio-02-141028100838-conversion-gate01/85/Fundamentos-de-geometria_espacial-sergio-02-22-320.jpg)
![(b) E E
= ;
(c) dois pontos A e B do espa¸co n˜ao pertencentes a est˜ao num mesmo semiespa¸co em
Aula 2 – Mais propriedades do espaço 23
rela¸c˜ao a se e somente se AB = ;
(d) dois pontos A e B n˜ao pertencentes a est˜ao em semiespa¸cos distintos (ou opostos)
em rela¸c˜ao a se e somente se AB .
N˜ao demonstraremos este teorema agora – sua demonstra¸c˜ao, cuja leitura ´e opcional, ser´a
apresentada na ´ultima se¸c˜ao desta aula – mas ´e preciso compreender bem o seu significado.
Para explic´a-lo melhor vamos estabelecer uma terminologia, an´aloga `a que vocˆes j´a viram
num curso de geometria plana em rela¸c˜ao a semiplanos:
Defini¸c˜ao 2.2. Se ´e um plano do espa¸co, o conjunto dos pontos de um semiespa¸co
determinado por que n˜ao est˜ao contidos em ´e um lado do espa¸co em rela¸c˜ao a . Os
lados do espa¸co correspondentes aos semiespa¸cos opostos s˜ao chamados de lados opostos em
rela¸c˜ao a .
Na figura 2.2 representamos a situa¸c˜ao descrita no teorema 2.1. Os pontos A e C est˜ao de
um mesmo lado do plano , enquanto que os pontos A e B, e A e D est˜ao em lados opostos.
Usando estes dados podemos concluir que CB . De fato, se CB = , ent˜ao, pelo
item (c) do teorema, os pontos C e B deveriam estar do mesmo lado do espa¸co em rela¸c˜ao
a . Ora, ent˜ao C est´a no mesmo semiespa¸co que A e no mesmo semiespa¸co que B, que
s˜ao semiespa¸cos distintos. Logo C pertence a ambos E e E
, contrariando o item (b) do
teorema, j´a que estamos supondo (implicitamente) que C .
Problema 2.4. Prove, adaptando a argumenta¸c˜ao apresentada no par´agrafo precedente que,
seguindo os dados representados na figura 2.2, BD = .
2.3 ˆAngulos e congruˆencia no espa¸co
Definimos em [7] um ˆangulo simplesmente como sendo um par de semirretas com origem
comum. Esta defini¸c˜ao n˜ao apresenta nenhum problema quando passamos a vˆe-la do ponto
de vista do espa¸co. No entanto devemos nos lembrar que ˆangulos s˜ao essencialmente objetos
planos. Por exemplo, temos a seguinte propriedade:
Figura 2.3: – Proposi¸c˜ao 2.3
Proposi¸c˜ao 2.3. Todo ˆangulo no espa¸co determina um ´unico plano.
Problema 2.5. Demonstre a proposi¸c˜ao 2.3 (a figura 2.3 d´a uma dica de como resolver
este problema).
Precisamos tomar cuidado, no entanto, com o conceito de regi˜ao angular. Para deixar
isto claro, transcrevemos a defini¸c˜ao de regi˜ao angular apresentada em [7] com as devidas
modifica¸c˜oes.
Fundamentos de Geometria Espacial.indd 23 28/01/2013 11:09:28](https://image.slidesharecdn.com/fundamentosdegeometriaespacial-sergio-02-141028100838-conversion-gate01/85/Fundamentos-de-geometria_espacial-sergio-02-23-320.jpg)
![Defini¸c˜ao 2.4. A regi˜ao angular determinada por um ˆangulo (n˜ao trivial) A = BAC ´e
o subconjunto
24 Fundamentos de geometria espacial
RA = l r,
onde ´e o plano determinado por A, B e C, l =
AB, r =
AC, l ´e o semiplano de relativo
a l que cont´em o ponto C, e r ´e o semiplano de relativo a r que cont´em o ponto B.
Os pontos pertencentes a RA que n˜ao pertencem aos lados de A s˜ao denominados pon-tos
interiores a A, e os pontos que n˜ao pertencem a RA e nem aos lados de A s ˜ao
denominados pontos exteriores a A.
Se D ´e um ponto interior a A dizemos que
AD divide ou separa o ˆangulo A.
Problema 2.6. Compare a defini¸c˜ao acima com a defini¸c˜ao de regi˜ao angular apresentada
em [7], apontando as diferen¸cas, e fa¸ca um desenho.
Observa¸c˜ao 2.1. As defini¸c˜oes de ˆangulo adjacente, ˆangulo raso e ˆangulo suplementar
tamb´em s˜ao todas relativas ao plano determinado pelo ˆangulo em quest˜ao, ou seja, s˜ao
objetos planos.
Se prestarmos aten¸c˜ao na defini¸c˜ao 2.4 e na observa¸c˜ao acima vemos que os axiomas III.1 e
III.2 do grupo III – axiomas sobre medidas de ˆangulos no plano – vistos em [7], s˜ao v´alidos
no espa¸co sem necessidade de adaptar seus enunciados. No entanto, o axioma III.3 precisa
de ser reescrito, como se segue.
Axioma III.3. Para toda semirreta
AB, todo n´umero real a tal que 0 a 180, e cada
plano contendo
AB existem exatamente duas semirretas
AD l e
AD ˜l tais que
m(BAD) = m(BAD) = a,
onde l =
AB e l, ˜l s˜ao semiplanos de em rela¸c˜ao a l.
Figura 2.4: – Axioma III.3
Na figura 2.4 representamos a situa¸c˜ao descrita no axioma III.3. No plano temos os pontos
D e D em lados opostos da reta l =
AB como no axioma III.3, isto ´e, tais que
m(BAD) = m(BAD) = a,
para um dado n´umero a com 0 a 180. Analogamente fica garantida a existˆencia de dois
pontos P e P num outro plano passando por l, com
m(BAP) = m(BAP) = a.
Fundamentos de Geometria Espacial.indd 24 28/01/2013 11:09:28](https://image.slidesharecdn.com/fundamentosdegeometriaespacial-sergio-02-141028100838-conversion-gate01/85/Fundamentos-de-geometria_espacial-sergio-02-24-320.jpg)
![Figura 2.5: – Caso LAL de congruˆencia de triˆangulos
Fechamos esta se¸c˜ao com algumas observa¸c˜oes sobre congruˆencias. No sistema axiom´atico
de geometria plana apresentado em [7] baseamos a ideia de congruˆencia na ideia de medida.
Estes conceitos, e os axiomas relativos, permanecem inalterados no nosso sistema para a
geometria espacial. Em particular, o axioma IV em [7], que postula o caso “lado-ˆangulo-lado”
(LAL) de congruˆencia de triˆangulos ´e v´alido tamb´em ao se comparar triˆangulos em
planos distintos. Por exemplo, na figura 2.5 representamos os triˆangulos ABC e PQR
nos planos e , respectivamente, tais que
Aula 2 – Mais propriedades do espaço 25
AB PQ
ABC PQR
BC QR
(LAL)
Nestas condi¸c˜oes, pelo caso LAL de congruˆencia de triˆangulos tem-se que ABC PQR.
Vamos agora resolver um problema de congruˆencia no espa¸co no exemplo a seguir.
Exemplo 2.1. Na figura 2.6 sabe-se que A, B, C e D s˜ao pontos n˜ao coplanares, e que B,
C e D est˜ao no plano . Se AB BC, AB BD e BC BD, demonstre que AC AD.
A
B
C
D
Figura 2.6: – Exemplo 2.1 e problema 2.7
Soluc¸˜ao: Os triˆangulos ABD e ABC s˜ao congruentes pelo caso LAL, pois
AB AB Lado comum aos triˆangulos;
ABD ABC ˆ Angulos retos, por hip´otese;
BD BC Lados congruentes, por hip´otese.
(LAL)
Logo os lados AD e AC s˜ao congruentes.
Resolva vocˆe o problema seguinte.
Problema 2.7. Novamente usando a figura 2.6 como referˆencia, suponha que DAB
CAB, AB BD e AB BC. Nestas condi¸c˜oes, prove que AD AC.
Fundamentos de Geometria Espacial.indd 25 28/01/2013 11:09:28](https://image.slidesharecdn.com/fundamentosdegeometriaespacial-sergio-02-141028100838-conversion-gate01/85/Fundamentos-de-geometria_espacial-sergio-02-25-320.jpg)
![2.4 O axioma das paralelas no espa¸co
Vimos em [7] que duas retas paralelas no plano s˜ao retas que n˜ao tˆem pontos em comum.
No espa¸co, por´em, temos outra situa¸c˜ao em que retas n˜ao tˆem pontos em comum, as retas
reversas:
26 Fundamentos de geometria espacial
Figura 2.7: – Retas reversas
Defini¸c˜ao 2.5. Duas retas no espa¸co s˜ao reversas se n˜ao est˜ao contidas em um mesmo
plano.
Na figura 2.7 representamos duas retas reversas. Para indicar em ilustra¸c˜oes que as retas s˜ao
reversas, sem a necessidade de tra¸car um plano, faremos como na figura 2.7b, onde queremos
expressar a ideia de que a reta r passa “por tr´as” da reta l em rela¸c˜ao `a nossa vis˜ao.
Problema 2.8. Como vocˆe demonstraria a existˆencia de retas reversas? Isto ´e, tome uma
reta r e um ponto P r e prove que por P passam retas reversas a r.
Problema 2.9. Sejam r e s duas retas reversas. Tome A r e B s e sejam o plano
determinado por r e B, e o plano determinado por s e A. Desenhe a situa¸c˜ao descrita e
diga quem ´e .
A defini¸c˜ao de retas paralelas fica assim:
Figura 2.8: – Retas paralelas
Defini¸c˜ao 2.6. Duas retas r e l no espa¸co s˜ao paralelas se s˜ao coplanares e n˜ao possuem
pontos em comum. Denotaremos esta rela¸c˜ao, como ´e tradicional, por r l.
O axioma das paralelas continua valendo.
Axioma V. Dada uma reta no espa¸co, por cada ponto que n˜ao lhe pertencente passa,
no m´aximo, uma reta paralela a ela.
Como todos devem se lembrar, na geometria plana demonstramos a existˆencia de retas
paralelas. Este fato (e sua demonstra¸c˜ao) s˜ao v´alidos no espa¸co. ´E
preciso apenas ter um
pequeno cuidado a mais.
Teorema 2.7. Sejam dados uma reta r e um ponto P fora de r. Ent˜ao existe uma ´unica
reta s passando por P e paralela a r.
Fundamentos de Geometria Espacial.indd 26 28/01/2013 11:09:28](https://image.slidesharecdn.com/fundamentosdegeometriaespacial-sergio-02-141028100838-conversion-gate01/85/Fundamentos-de-geometria_espacial-sergio-02-26-320.jpg)
![Demonstrac¸˜ao. Reduzimos o problema no espa¸co a um problema no plano: seja o plano
determinado por r e P, e tome s a reta paralela a r passando por P, cuja existˆencia ´e
garantida pelo que foi visto em geometria plana. A unicidade segue do axioma V.
Problema 2.10. Reveja a demonstra¸c˜ao da existˆencia de retas paralelas em um texto de
fundamentos geometria plana, como [7], por exemplo.
Duas retas paralelas determinam um ´unico plano. Vamos registrar este fato como uma
proposi¸c˜ao.
Proposi¸c˜ao 2.8. Por duas retas paralelas r e l passa um ´unico plano.
Demonstrac¸˜ao. Observe que, por defini¸c˜ao, as retas paralelas r e l est˜ao contidas em um
plano . Suponha que exista um outro plano contendo r e l. Se P ´e um ponto de l,
ent˜ao ´e determinado por r e P. Mas tamb´em ´e determinado por r e P donde, pelo
problema 1.3, = .
V´arias propriedades que as retas paralelas obedecem no plano se transferem para o espa¸co.
Uma das mais importantes ´e a transitividade que registramos no teorema a seguir, cuja
demonstra¸c˜ao ser´a apresentada na se¸c˜ao 2.5.
Aula 2 – Mais propriedades do espaço 27
t
r
s
Figura 2.9: – Teorema 2.9
Teorema 2.9. Se r, s e t s˜ao retas tais que r s e s t ent˜ao r t.
Apresentamos a seguir um exemplo de aplica¸c˜ao deste teorema.
Exemplo 2.2. Em geometria plana prova-se o seguinte resultado: dado um quadril´atero
qualquer ABCD num plano, os pontos m´edios de seus lados s˜ao v´ertices de um paralelo-gramo.
O mesmo resultado vale se os v´ertices do quadril´atero n˜ao s˜ao coplanares (veja a
figura 2.10)
De fato, tome 4 pontos A, B, C e D n˜ao coplanares, e seja o plano determinado por A, B
e D. Sejam M, N, P e Q os pontos m´edios dos lados AB, BC, CD e DA, respectivamente.
Ent˜ao temos, no triˆangulo ABD, que
MP BD e MP = BD
2
.
Fundamentos de Geometria Espacial.indd 27 28/01/2013 11:09:29](https://image.slidesharecdn.com/fundamentosdegeometriaespacial-sergio-02-141028100838-conversion-gate01/85/Fundamentos-de-geometria_espacial-sergio-02-27-320.jpg)
![28 Fundamentos de geometria espacial
A
B
D
C
O
N
P
M
Figura 2.10: – Exemplo 2.2
Analogamente, no triˆangulo BCD temos
ON BD e ON = BD
2
.
Assim temos que
(i) MP BD e ON BD MP ON, pelo teorema anterior. Em particular,
MP e
ON s˜ao coplanares, ou seja, os quatro pontos m´edios pertencem a um mesmo plano.
(ii) MP ON.
Provamos ent˜ao que MNOP ´e um quadril´atero contido num plano com dois lados paralelos
e congruentes, donde ´e um paralelogramo.
Problema 2.11. Reveja as demonstra¸c˜oes dos fatos sobre paralelogramos utilizados no
exemplo acima em [7] ou outra fonte qualquer.
2.5 Opcional: demonstra¸c˜ao dos teoremas 2.1 e 2.9
Apresentamos nesta se¸c˜ao as demonstra¸c˜oes dos teoremas 2.1 e 2.9, cuja leitura ´e opcional.
Come¸camos pelo teorema 2.1.
Demonstrac¸˜ao. (Teorema 2.1) Sejam um plano e P um ponto (existe o ponto
P pelo axioma I.8). Vamos “construir” os conjuntos E e E
e provar que satisfazem as
propriedades enunciadas, seguindo os passos abaixo.
(1) Definamos E e E
da seguinte forma:
E = pontos X do espa¸co tais que XP = {P}
E
= pontos X do espa¸co tais que XP
Observe que E , pois P E. Para verificar que E
tome Q (pelo axioma
I.5) e na reta
PQ tome R tal que P −Q − R2. Assim R E
(veja figura 2.11).
2Lembramos que em [7] usamos a nota¸c˜ao P − Q − R para indicar que o ponto Q est´a entre P e R, isto ´e,
que o ponto Q pertence ao interior do segmento PR. Em particular, a existˆencia de R ´e garantida pelo
axioma II.3 de [7].
Fundamentos de Geometria Espacial.indd 28 28/01/2013 11:09:29](https://image.slidesharecdn.com/fundamentosdegeometriaespacial-sergio-02-141028100838-conversion-gate01/85/Fundamentos-de-geometria_espacial-sergio-02-28-320.jpg)

![30 Fundamentos de geometria espacial
P
A
l
B
(a)
P
A
l
B
(b)
P
(d)
P
l
A
B
(c)
A
B
Figura 2.12
A an´alise de (d) ´e inteiramente an´aloga `a realizada para (c) bastando trocar a express˜ao
“n˜ao interceptam” por “interceptam”, e vice-versa, nos locais adequados. Deixamos este
exerc´ıcio ao leitor.
Agora passamos `a demonstra¸c˜ao do teorema 2.9.
t
Q
l
P
r
s
Figura 2.13: – Demonstra¸c˜ao do teorema 2.9
Demonstrac¸˜ao. (Teorema 2.9) O caso em que as retas r, s e t s˜ao coplanares j´a foi provado
em [7]. Vamos estudar ent˜ao o caso em que as trˆes retas n˜ao s˜ao coplanares. Acompanhe os
passos abaixo na figura 2.13.
Fundamentos de Geometria Espacial.indd 30 28/01/2013 11:09:29](https://image.slidesharecdn.com/fundamentosdegeometriaespacial-sergio-02-141028100838-conversion-gate01/85/Fundamentos-de-geometria_espacial-sergio-02-30-320.jpg)















![46 Fundamentos de geometria espacial
Figura 4.2
No espa¸co temos ainda o caso de retas reversas, que n˜ao s˜ao nem concorrentes nem paralelas.
Como poder´ıamos medir o ˆangulo entre elas? Bem, poder´ıamos fazer o seguinte: “colocar”
uma delas sobre a outra utilizando retas paralelas. Explicando melhor, se r e s s˜ao reversas,
tomamos, por exemplo, s uma reta concorrente com r e paralela a s, e definimos a medida
do ˆangulo entre r e s como sendo a medida do ˆangulo entre r e s. A ideia parece boa?
Bem, pode ser que sim, mas temos que verificar que independe da escolha das retas paralelas
auxiliares. Dito de outra forma, se, por exemplo, r for uma reta paralela a r e concorrente
com s, ser´a que m((r, s)) = m((r, s))? De fato, isto acontece, como enunciamos em
nosso pr´oximo teorema (veja a figura 4.2).
Teorema 4.1. Sejam r, s e r, s dois pares de retas concorrentes tais que r r e s s.
Ent˜ao m((r, s)) = m((r, s)).
Figura 4.3
Na figura 4.3 representamos a situa¸c˜ao do teorema 4.1. Temos, na figura, que a = (r, s)
e b = (r, s) onde r r e s s. O teorema nos diz ent˜ao que a b. Procure
entender bem o significado deste teorema, que ´e bem intuitivo. A sua demonstra¸c˜ao, de
leitura opcional, ser´a apresentada na se¸c˜ao 4.5.
Problema 4.1. Demonstre o teorema 4.1 no caso em que r, s, r e s s˜ao coplana-res.(
Sugest˜ao: consulte um livro de geometria plana como, por exemplo, [7].)
Corol´ario 4.2. Sejam r e s retas reversas. Se r r e s s s˜ao retas tais que r ´e
concorrente a s e s ´e concorrente a r, ent˜ao
m((r, s)) = m((r, s)).
Problema 4.2. Demonstre, usando o teorema 4.1, o corol´ario acima (veja a figura 4.2).
Agora podemos definir a medida de ˆangulos entre retas reversas.
Defini¸c˜ao 4.3. Sejam r e s duas retas reversas no espa¸co. Definimos a medida do ˆangulo
entre r e s, denotada por m((r, s)), como sendo m((r, s)), onde s ´e uma reta paralela
a s e concorrente a r.
Fundamentos de Geometria Espacial.indd 46 28/01/2013 11:09:35](https://image.slidesharecdn.com/fundamentosdegeometriaespacial-sergio-02-141028100838-conversion-gate01/85/Fundamentos-de-geometria_espacial-sergio-02-46-320.jpg)












![AUla 5: As Ângulos entre planos 59
AULA5: ˆANGULOS ENTRE PLANOS
OBJETIVOS
Introduzir o conceito de ˆangulos entre planos: os diedros. Estudar o perpendicularismo
entre planos.
5.1 Introdu¸c˜ao
Na aula anterior estudamos um pouco sobre ˆangulos entre retas no espa¸co, e tamb´em es-tudamos
perpendicularismo entre retas e planos. A pr´oxima etapa ´e estudar ˆangulos entre
retas e planos e ˆangulos entre planos. Veremos que existe um conceito de “ˆangulo” no espa¸co
inteiramente an´alogo ao de ˆangulo no plano, um “ˆangulo” cujos lados s˜ao semiplanos.
5.2 ˆAngulos entre planos: diedros
Em [7] definimos um ˆangulo como um par de semirretas com origem comum. Podemos, de
maneira natural, estender este conceito para planos no espa¸co, isto ´e, podemos “tridimensi-onalizar”
o ˆangulo determinado por semirretas. Chamamos a vers˜ao de ˆangulo para planos
de diedro, conforme a defini¸c˜ao mais abaixo. De agora em diante, para facilitar a exposi¸c˜ao,
indicaremos semiplanos com um sinal de chap´eu; por exemplo, ˆ indica um semiplano do
plano .
ˆ
ˆ
l
Figura 5.1
Defini¸c˜ao 5.1. Um diedro1 ´e a uni˜ao de dois semiplanos com a mesma reta de origem.
Dizemos que os semiplanos que determinam o diedro s˜ao suas faces, e a reta comum aos
semiplanos a sua aresta.
O diedro determinado pelos semiplanos ˆ e ˆ ser´a denotado por (ˆ, ˆ ), onde ˆ e ˆ s ˜ao
suas faces.
Um bom modelo de diedro ´e um livro ou caderno aberto parcialmente. As p´aginas opos-tas
s˜ao suas faces, e a sua aresta ´e o encontro das mesmas na lombada. Na figura 5.1
representamos um diedro formado pelos semiplanos ˆ e ˆ com aresta l.
1A palavra diedro significa “dois lados”, ou “duas faces”, do grego di- = dois, e -edro = cadeira, face.
Fundamentos de Geometria Espacial.indd 59 28/01/2013 11:09:39](https://image.slidesharecdn.com/fundamentosdegeometriaespacial-sergio-02-141028100838-conversion-gate01/85/Fundamentos-de-geometria_espacial-sergio-02-59-320.jpg)










![70 Fundamentos de geometria espacial
Figura 6.1
Problema 6.1. Sejam A, e P como na defini¸c˜ao 6.2, com A . Mostre que dist(A,) =
AP AQ para todo ponto Q distinto de P. (Sugest˜ao: na figura 6.1 o triˆangulo APQ
´e retˆangulo)
Passemos agora ao estudo de distˆancia entre planos. Lembremos a defini¸c˜ao de distˆancia
entre retas num plano:
Defini¸c˜ao 6.3. A distˆancia entre duas retas r e s coplanares ´e o n´umero dist(r, s) definido
da seguinte maneira:
(i) dist(r, s) = 0 se r e s s˜ao concorrentes;
(ii) dist(r, s) = dist(A, s) para algum ponto A r, se r e s s˜ao paralelas.
Traduzimos facilmente esta defini¸c˜ao para o caso de distˆancia entre planos:
Defini¸c˜ao 6.4. A distˆancia entre dois planos e ´e o n´umero dist(, ) definido da
seguinte maneira:
(i) dist(, ) = 0 se e s˜ao concorrentes;
(ii) dist(, ) = dist(A, ) para algum ponto A , se e s˜ao paralelos.
Figura 6.2
A propriedade que garante que a defini¸c˜ao acima ´e “boa”, isto ´e, que tem um sentido
adequado, ´e a propriedade descrita no problema seguinte, inteiramente an´aloga `a que garante
o bom sentido da defini¸c˜ao 6.3 (veja [7]).
Fundamentos de Geometria Espacial.indd 70 28/01/2013 11:09:43](https://image.slidesharecdn.com/fundamentosdegeometriaespacial-sergio-02-141028100838-conversion-gate01/85/Fundamentos-de-geometria_espacial-sergio-02-70-320.jpg)
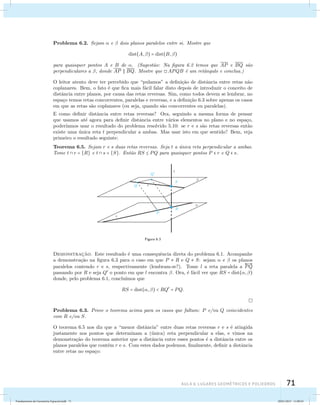


![6.4 Alguns lugares geom´etricos
Nesta se¸c˜ao vamos apresentar alguns lugares geom´etricos. Lembramos que um lugar geom´etrico
´e, em termo simples, o conjuntos dos pontos (agora no espa¸co) que satisfazem a alguma pro-priedade
preestabelecida. Come¸camos mostrando que os planos bissetores s˜ao, em verdade,
lugares geom´etricos, assim como as bissetrizes no plano (reveja o assunto em algum livro de
geometria plana, como [7]).
Problema 6.6. Seguindo as nota¸c˜oes da figura 6.5, mostre que o lugar geom´etrico dos
pontos equidistantes de e ´e justamente a uni˜ao dos planos bissetores 1 e 2.
Soluc¸˜ao. Novamente uma propriedade an´aloga `a de bissetrizes, que recordamos aqui: o
lugar geom´etrico dos pontos equidistantes de duas retas concorrentes ´e justamente a uni˜ao
das bissetrizes dos ˆangulos por elas formados. E a t´atica para resolver o problema ´e a mesma
do problema anterior: reduzi-lo ao caso plano.
PH . Reduzimos assim o problema ao caso de um ˆangulo plano. A situa¸c˜ao ´e ilustrada
na figura 6.7, onde representamos o plano e os elementos acima descritos. Observe que s1
´e a bissetriz de um dos ˆangulos determinados por a e b, e que
74 Fundamentos de geometria espacial
Figura 6.7
Primeiro provemos que se P 1 2 ent˜ao dist(P,) = dist(P, ). Sem perda de generali-dade,
tomemos P 1. Seja o plano passando por P e perpendicular `a reta l, na qual se
cortam os planos e . Usando as nota¸c˜oes do problema 6.5, tomamos
a = , b = , s1 = 1 e s2 = 2.
Sejam G a e H b tais que PG a e PH b. Temos que, como e , ent˜ao
PG
e
dist(P,) = PG, dist(P, ) = PH,
donde, pelo resultado j´a conhecido num plano, PG = PH, ou seja,
dist(P,) = dist(P, ).
Passemos `a rec´ıproca, isto ´e, provemos que se P ´e um ponto equidistante de e , ent˜ao
P 1 2. Primeiro observe que P deve pertencer a alguma das quatro regi˜oes diedrais
determinadas por e (em outras palavras, P n˜ao pode pertencer a nenhum dos dois
planos – justifique esta afirma¸c˜ao). Tome ent˜ao o plano passando por P e perpendicular
Fundamentos de Geometria Espacial.indd 74 28/01/2013 11:09:44](https://image.slidesharecdn.com/fundamentosdegeometriaespacial-sergio-02-141028100838-conversion-gate01/85/Fundamentos-de-geometria_espacial-sergio-02-74-320.jpg)










![aula 7 : Volumes de poliedros 85
AULA7: VOLUMES DE POLIEDROS
OBJETIVOS
Introduzir o conceito de volumes de s´olidos geom´etricos, mais especificamente de regi˜oes
poliedrais. Apresentar um sistema de princ´ıpios que estabele¸ca com rigor adequado este
conceito; neste sistema inclui-se o Princ´ıpio de Cavalieri. Calcular o volume de alguns
s´olidos apresentados na aula anterior.
7.1 Introdu¸c˜ao
Nesta aula estudaremos o conceito de volume e calcularemos os volumes de alguns s´olidos. O
procedimento ´e an´alogo ao que foi feito para apresentar o conceito de ´area de figuras planas
em [7]. Queremos medir o “tanto” que um objeto espacial ocupa um lugar no espa¸co. Este
“tanto” ´e o que chamaremos de volume1.
Figura 7.1
Vejamos um exemplo. Na figura 7.1 representamos um paralelep´ıpedo cujas arestas medem
8, 4 e 4. Cortamos ent˜ao o paralelep´ıpedo com v´arios planos paralelos, formando pequenos
cubos de aresta 1. Ent˜ao o paralelep´ıpedo ´e formado de 8 × 4 × 4 = 128 destes cubos.
Assim poder´ıamos dizer que o “tanto” (= volume) que o paralelep´ıpedo ocupa no espa¸co ´e
equivalente a 128 cubos de aresta 1. Se dissermos que o volume do cubo de aresta 1 ´e 1,
ent˜ao o volume do paralelep´ıpedo seria 128.
No exemplo acima apresentamos um paralelep´ıpedo cujas arestas tˆem comprimentos inteiros.
E se n˜ao for assim? Bem, se as arestas possu´ıssem comprimentos racionais, ainda seria
poss´ıvel dividir o paralelep´ıpedo em cubos iguais com lados racionais. Por exemplo, se as
arestas medissem 34, 57 e 23, ent˜ao podemos dividi-lo em 3 × 5 × 2 = 30 cubos de aresta
184 (verifique!); e ent˜ao poder´ıamos dizer que o volume do paralelep´ıpedo corresponde ao
volume de 30 cubos de aresta 184, ou que o seu volume ´e 3084 = 521. Se as arestas do
paralelep´ıpedo n˜ao tiverem todas medidas racionais, podemos tomar aproxima¸c˜oes racionais
destas medidas e, atrav´es de um processo de limite, mostrar que ´e razo´avel afirmar que o
volume de um paralelep´ıpedo ´e dado pelo produto das medidas de suas arestas.
E como poder´ıamos fazer para medir o volume de figuras mais gerais, como prismas que n˜ao
sejam paralelep´ıpedos, pirˆamides, etc.? Poder´ıamos “aproximar” a figura atrav´es de blocos
1Deixaremos, daqui por diante, a palavra “volume” em it´alico, at´e que apresentemos este conceito com mais
precis˜ao.
Fundamentos de Geometria Espacial.indd 85 28/01/2013 11:09:48](https://image.slidesharecdn.com/fundamentosdegeometriaespacial-sergio-02-141028100838-conversion-gate01/85/Fundamentos-de-geometria_espacial-sergio-02-85-320.jpg)
![86 Fundamentos de geometria espacial
Figura 7.2
de paralelep´ıpedos, como mostramos na figura 7.2 e, atrav´es de um processo de limite,
aumentando o n´umero de paralelep´ıpedos, calcular o volume da figura2. No entanto n˜ao
utilizaremos este procedimento, mas um outro equivalente, conhecido como Princ´ıpio de
Cavalieri, que introduziremos mais adiante.
Para finalizar esta introdu¸c˜ao chamamos a aten¸c˜ao para o seguinte: poder´ıamos apresentar
o conceito de volume com o mesmo rigor com que se apresenta o conceito de ´area de figuras
planas, utilizando uma s´erie de axiomas (veja em [7], por exemplo), mas preferimos trabalhar
de forma mais intuitiva pois, caso contr´ario, o assunto atinge complica¸c˜oes que est˜ao al´em
de um texto introdut´orio como este.
7.2 Volume de regi˜oes poliedrais
Como j´a dissemos na introdu¸c˜ao, n˜ao daremos neste texto um tratamento completamente
formal da teoria de volumes de figuras espaciais, mas procuraremos, nesta se¸c˜ao, apresentar
de maneira sucinta como este tratamento poderia ser feito. Por isto enunciaremos as propri-edades
que o volume de regi˜oes poliedrais deve satisfazer com o t´ıtulo de princ´ıpios, e n˜ao
de axiomas, como seria usual.
Figura 7.3
A primeira pergunta que surge ´e: o que ´e, de fato, uma regi˜ao poliedral? Podemos definir este
conceito de maneira inteiramente an´aloga `a defini¸c˜ao usual de regi˜ao poligonal3: uma regi˜ao
poliedral ´e uma uni˜ao finita de tetraedros que n˜ao tˆem pontos interiores em comum, onde os
2O leitor atento pode perceber que este procedimento nada mais ´e do que uma forma de c´alculo integral.
3Veja em [7] ou outro texto qualquer de geometria plana como s˜ao definidas regi˜oes poligonais
Fundamentos de Geometria Espacial.indd 86 28/01/2013 11:09:49](https://image.slidesharecdn.com/fundamentosdegeometriaespacial-sergio-02-141028100838-conversion-gate01/85/Fundamentos-de-geometria_espacial-sergio-02-86-320.jpg)
![pontos interiores de um tetraedro s˜ao os pontos do espa¸co que pertencem simultaneamente
a todas as seis regi˜oes diedrais determinadas pelas faces do tetraedro. De agora para frente
utilizaremos o termo poliedro no sentido de regi˜ao poliedral.
Todas as figuras espaciais apresentadas na se¸c˜ao 6.5 da aula anterior, `a exce¸c˜ao dos triedros,
podem ser seccionadas em um n´umero finito de tetraedros. Na figura 7.3 apresentamos uma
divis˜ao de um cubo em cinco tetraedros, e na figura 7.4, a divis˜ao de um octaedro em quatro
tetraedros.
aula 7 : Volumes de poliedros 87
Figura 7.4
Nosso primeiro princ´ıpio ´e o da existˆencia:
Princ´ıpio da Existˆencia do Volume. A cada regi˜ao poliedral R est´a associado um
´unico n´umero real positivo, denotado por V(R), chamado de volume do poliedro R.
Se um poliedro ´e seccionado em v´arios poliedros que n˜ao tˆem pontos interiores em comum4,
´e natural assumir que o volume do poliedro ´e igual `a soma dos volumes dos poliedros em
que foi seccionado.
Princ´ıpio da Soma de Volumes. Se o poliedro R se decomp˜oe na forma
R = R1 R2 . . . Rn,
onde Ri s˜ao poliedros que n˜ao possuem pontos interiores em comum, ent˜ao
V(R) = V(R1) + V(R2) + . . . + V(Rn).
Precisamos agora dar uma “referˆencia” para o c´alculo de volumes. No caso de ´areas a
referˆencia utilizada em geral ´e a ´area de um quadrado (veja, por exemplo, em [7]). No
espa¸co o natural ´e utilizar paralelep´ıpedos retangulares, como foi discutido na introdu¸c˜ao.
Princ´ıpio da Unidade para Volumes. O volume de um paralelep´ıpedo retangular ´e
o produto dos comprimentos de suas trˆes arestas n˜ao paralelas que se encontram em um
mesmo v´ertice.
Na figura 7.5 representamos um paralelep´ıpedo retˆangulo cujo volume ´e V = a.b.h, pelo
princ´ıpio da unidade para volumes, onde AB = a, BC = b e BG = h.
4N˜ao definimos formalmente o que s˜ao pontos interiores de poliedros, mas apenas o que s˜ao pontos interiores
de tetraedros. Essencialmente, um ponto interior de um poliedro ´e um ponto interior de um dos
tetraedros que o comp˜oe.
Fundamentos de Geometria Espacial.indd 87 28/01/2013 11:09:49](https://image.slidesharecdn.com/fundamentosdegeometriaespacial-sergio-02-141028100838-conversion-gate01/85/Fundamentos-de-geometria_espacial-sergio-02-87-320.jpg)



























![APˆENDICE A: AXIOMAS DA GEOMETRIA PLANA
Listamos neste apˆendice todos os axiomas e algumas defini¸c˜oes b´asicas apresentados em [7],
para facilitar a consulta dos leitores.
A.1 Axiomas: grupo I, axiomas de incidˆencia
Axioma I.1. Se A e B s˜ao dois pontos distintos do plano, ent˜ao existe uma e uma ´unica
reta l tal que A e B pertencem a l.
Axioma I.2. Toda reta do plano possui pelo menos dois pontos distintos.
Axioma I.3. O plano cont´em pelo menos trˆes pontos distintos que n˜ao pertencem a uma
mesma reta.
A.2 Axiomas: grupo II, parte 1: m´etrica e ordem na
Apêndices: AXIOMAS DA GEOMETRIA PLANA 115
reta
Axioma II.1. Para cada par de pontos A, B do plano existe um ´unico n´umero real asso-ciado,
denotado por AB, satisfazendo as propriedades:
(a) AB 0;
(b) AB = 0 se e somente se A = B;
(c) AB = BA.
Defini¸c˜ao A.1. A distˆancia entre dois pontos A e B do plano ´e o n´umero AB postulado
no axioma II.1.
Defini¸c˜ao A.2. Dados dois pontos A e B diremos que um ponto C est´a entre A e B se:
(a) C
AB;
(b) AB = AC + BC.
Esta rela¸c˜ao ser´a denotada por A − C − B.
Axioma II.2. Se A, B e C s˜ao trˆes pontos alinhados, ent˜ao um deles est´a entre os outros
dois.
Defini¸c˜ao A.3. O conjunto
dos pontos que est˜ao entre dois pontos A e B, incluindo estes,
´e um segmento (da reta
AB), e ser´a denotado por AB, ou seja,
AB = {pontos C tais que A − C − B} {A,B}.
Os pontos A e B s˜ao os extremos de AB, e qualquer outro ponto do intervalo distinto de seus
extremos ´e um ponto interior de AB. Analogamente, todo ponto do plano que n˜ao pertence
a AB ´e um ponto exterior ao segmento. O comprimento ou medida do segmento AB ´e a
distˆancia entre os seus extremos, ou seja, ´e o n´umero AB.
Fundamentos de Geometria Espacial.indd 115 28/01/2013 11:10:00](https://image.slidesharecdn.com/fundamentosdegeometriaespacial-sergio-02-141028100838-conversion-gate01/85/Fundamentos-de-geometria_espacial-sergio-02-115-320.jpg)



![RReeffeerrˆeˆenncicaisas Bibliogr´aficas
[1] J. L. M. Barbosa, Geometria Euclidiana Plana, SBM, Rio de Janeiro, 1985.
[2] P. C. P. Carvalho, Introdu¸c˜ao `a Geometria Espacial, 4a ed., SBM, Rio de Janeiro,
2005.
[3] O. Dolce J. N. Pompeo, Fundamentos de Matem´atica Elementar, vol 9: Geome-tria
Plana, 6a ed., Atual Editora, S˜ao Paulo, 1990.
[4] O. Dolce J. N. Pompeo, Fundamentos de Matem´atica Elementar, vol 10: Geo-metria
Espacial, posi¸c˜ao e m´etrica, 6a ed., Atual Editora, S˜ao Paulo, 2005.
[5] F. L. Downs, Jr. E. E. Moise, Geometria Moderna, 2 volumes, Ed. Edgar Blucher,
S˜ao Paulo, 1971.
[6] M .C. de Farias. Resolu¸c˜ao de Problemas Geom´etricos, Ed. UFMG, Belo Horizonte,
2009.
[7] P. A. F. Machado. Fundamentos de Geometria Plana, preprint, 2010.
[8] A. V. Pogorelov, Geometr´ıa elemental, trad. para o espanhol por Carlos Vega, Ed.
Mir, Moscou, 1974.
[9] M. L. B. de Queiroz E. Q. F. Rezende, Geometria Euclidiana Plana e Cons-tru
¸c˜oes Geom´etricas, 2a ed., Ed. da Unicamp, Campinas, 2008.
119
Reefrêacins 119
Fundamentos de Geometria Espacial.indd 119 28/01/2013 11:10:01](https://image.slidesharecdn.com/fundamentosdegeometriaespacial-sergio-02-141028100838-conversion-gate01/85/Fundamentos-de-geometria_espacial-sergio-02-119-320.jpg)
