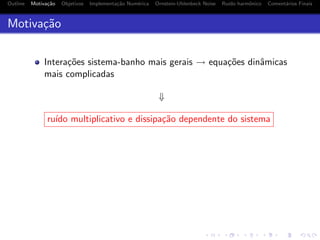
O documento discute a motivação para estudar equações dinâmicas do tipo Langevin com ruído colorido em teoria de campos. Esse tipo de equação surge quando se leva em conta interações mais realistas entre um sistema e um banho térmico, resultando em termos não-Markovianos e ruído colorido. O documento também apresenta uma possível abordagem numérica para resolver numericamente tais equações.








![Outline Motiva¸c˜ao Objetivos Implementa¸c˜ao Num´erica Ornstein-Uhlenbeck Noise Ru´ıdo harmˆonico Coment´arios Finais
Motiva¸c˜ao
¨q(t) +
t
0
dt γ(t − t )˙q(t ) + V [q(t)] = ξ(t) (1)
γ(t − t ) = Θ(t − t )
1
M
N
α=1
c2
α
mαω2
α
cos(ωαt)
⇒ Equa¸c˜ao n˜ao-Markoviana (kernel n˜ao-local γ(t − t ), possui
mem´oria da hist´oria passada) com ru´ıdo gaussiano e colorido:
ξ(t) ρ
(0)
B
= 0, ξ(t)ξ(t ) ρ
(0)
B
= kBTγ(t − t )](https://image.slidesharecdn.com/slidesccp2008v1-130501132312-phpapp01/85/Efeitos-de-memoria-em-teoria-de-campos-11-320.jpg)

![Outline Motiva¸c˜ao Objetivos Implementa¸c˜ao Num´erica Ornstein-Uhlenbeck Noise Ru´ıdo harmˆonico Coment´arios Finais
Motiva¸c˜ao
Exemplo:
L =
1
2
(∂µφ)2
−
1
2
m2
φφ2
−
λ
4!
φ4
+
1
2
(∂µχ)2
−
1
2
m2
χχ2
−
g2
4
φχ2
+ Lσ[χ, σj ]
Lσ[χ, σj ] inclui vari´aveis de campo adicionais que podem estar
acopladas a χ.
φ → campo cl´assico cuja dinˆamica estamos interessados
χ → campo quˆantico termalizado `a alguma temperatura T
A¸c˜ao efetiva para φ determinada integrando o campo χ](https://image.slidesharecdn.com/slidesccp2008v1-130501132312-phpapp01/85/Efeitos-de-memoria-em-teoria-de-campos-14-320.jpg)
![Outline Motiva¸c˜ao Objetivos Implementa¸c˜ao Num´erica Ornstein-Uhlenbeck Noise Ru´ıdo harmˆonico Coment´arios Finais
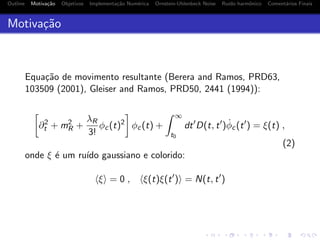
Motiva¸c˜ao
Rela¸c˜ao entre D(t − t ) e N(t − t ): teorema de flutua¸c˜ao-dissipa¸c˜ao
generalizado no espa¸co de fourier(Berera, Moss and Ramos. PRD76,
083520 (2007)):
N(ω) = 2ω n(ω) +
1
2
D(ω) .
onde n(ω) = [exp(βω) − 1]
−1
.
No regime cl´assico, ω T
2ω [n(ω) + 1/2] → 2T
⇒ reobtemos o teorema de flutua¸c˜ao-dissipa¸c˜ao cl´assico.](https://image.slidesharecdn.com/slidesccp2008v1-130501132312-phpapp01/85/Efeitos-de-memoria-em-teoria-de-campos-16-320.jpg)
![Outline Motiva¸c˜ao Objetivos Implementa¸c˜ao Num´erica Ornstein-Uhlenbeck Noise Ru´ıdo harmˆonico Coment´arios Finais
Motiva¸c˜ao
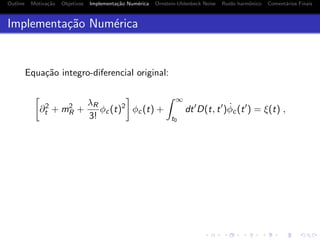
Forma gen´erica do kernel de dissipa¸c˜ao em 0-d:
D(t, t ) = #1 e−τ−1
χ (t−t )
+ e−τ−1
χ (t−t )
#2 cos[mχ(t − t )] + #3 sin[mχ(t − t )]
τχ → tempo de relaxa¸c˜ao do banho t´ermico.
Alterando a intera¸c˜ao sistema-banho (p. ex ∼ φ2χ2) podemos
obter ru´ıdo multiplicativo na equa¸c˜ao de movimento.](https://image.slidesharecdn.com/slidesccp2008v1-130501132312-phpapp01/85/Efeitos-de-memoria-em-teoria-de-campos-17-320.jpg)








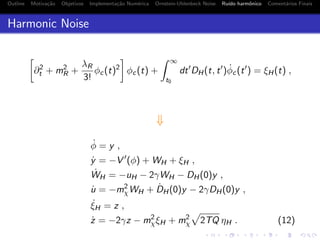
![Outline Motiva¸c˜ao Objetivos Implementa¸c˜ao Num´erica Ornstein-Uhlenbeck Noise Ru´ıdo harmˆonico Coment´arios Finais
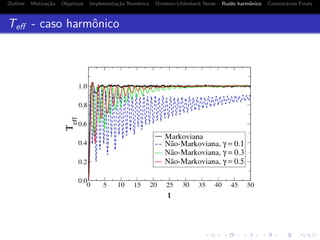
Ru´ıdo harmˆonico
∂2
t + m2
R +
λR
3!
φc(t)2
φc(t) +
∞
t0
dt DH(t, t ) ˙φc(t ) = ξH(t) ,
(9)
onde o kernel n˜ao-local DH (t − t ) ´e dado por
DH(t−t ) = e−γ(t−t )
Qm2
χ
2γ
cos[Ω1(t − t )] +
γ
Ω1
sin[Ω1(t − t )] ,
(10)
e ξH(t) ´e um ru´ıdo gaussiano colorido que satisfaz
ξH(t) = 0 ,
ξH(t)ξH(t ) = TDH(t − t ) . (11)](https://image.slidesharecdn.com/slidesccp2008v1-130501132312-phpapp01/85/Efeitos-de-memoria-em-teoria-de-campos-27-320.jpg)