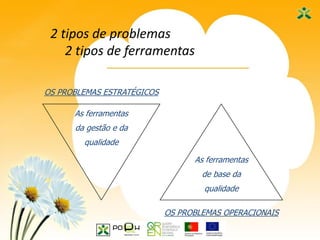
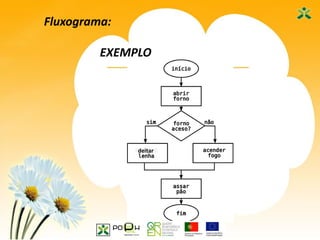
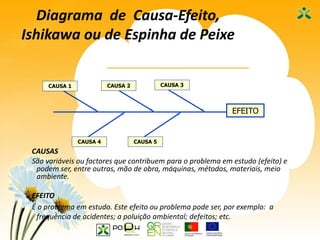
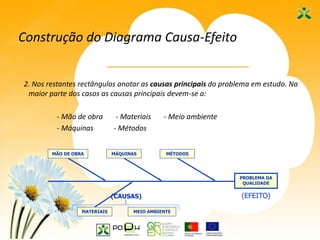
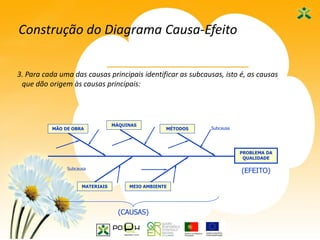
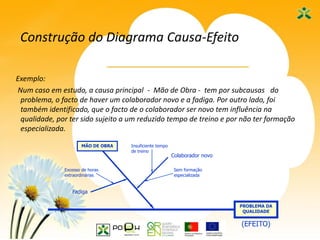
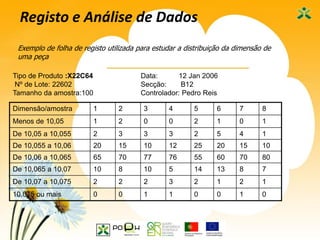
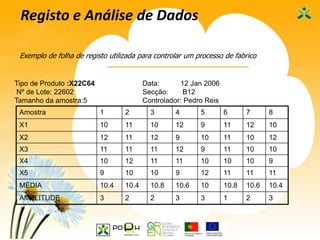
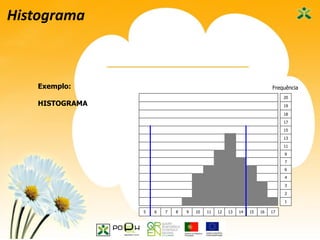
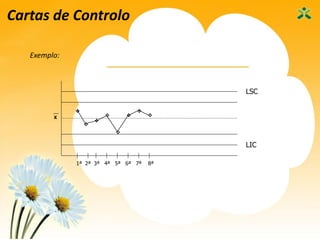
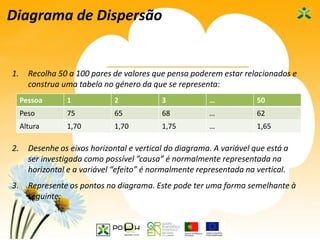
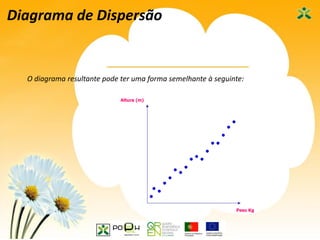
Este documento apresenta as sete ferramentas clássicas da qualidade, descrevendo seus objetivos e como aplicá-las. As ferramentas incluem fluxogramas, registros e análise de dados, diagramas de Ishikawa, diagramas de Pareto, histogramas, cartas de controle e diagramas de dispersão.