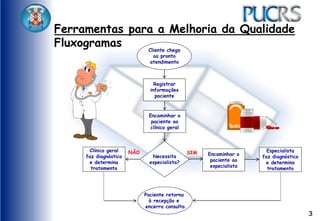
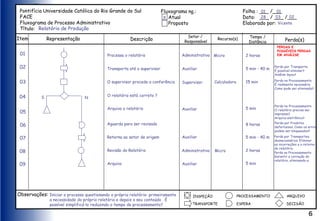
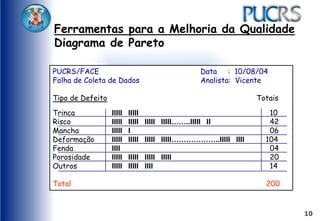
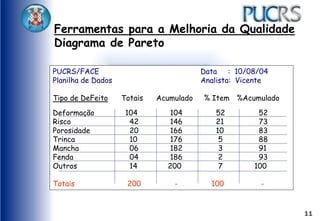
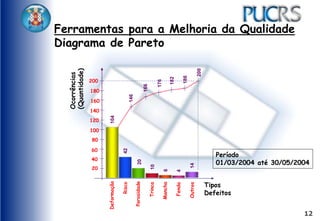
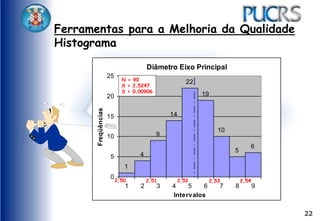
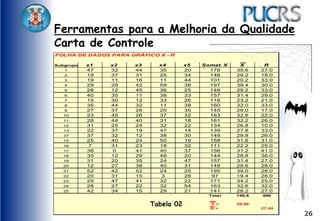
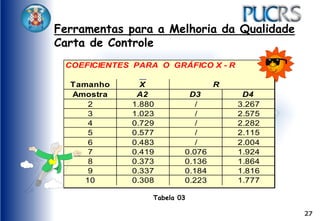
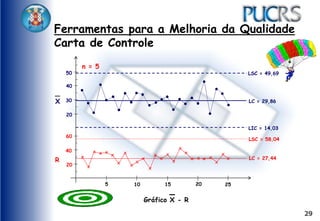
O documento apresenta ferramentas para melhoria da qualidade, como fluxogramas, diagramas de Pareto e de Ishikawa, que ajudam a analisar e otimizar processos. Ele detalha etapas de comunicação, coleta de dados, análise e documentação, além de sugerir métodos para identificação de problemas e suas causas. Exemplos práticos e técnicas de coleta de dados são fornecidos para ilustrar os conceitos.