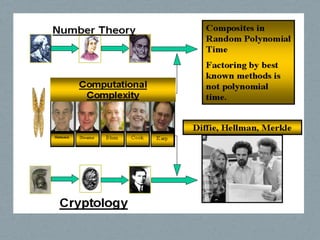
1) O documento discute a história e os conceitos fundamentais da criptografia moderna, incluindo o desenvolvimento das chaves públicas e sistemas como RSA. 2) A criptografia de chave pública permitiu a troca segura de chaves sem comunicação prévia secreta, revolucionando a segurança digital. 3) A segurança da criptografia moderna depende de problemas matemáticos computacionalmente difíceis, como fatoração de inteiros e logaritmo discreto, cuja resolução em tempo polinomial por computadores quânticos ameaç

1. Criptografia Moderna:
Matemática para a Segurança Digital
Ruy J.G.B. de Queiroz
Centro de Informática
UFPE

2. Bitcoin:
Uma Cripto-Moeda

3. História da Bitcoin
(Wikipédia)
• “Bitcoin é uma das primeiras implementações de um
conceito chamado cripto-moeda.
• Baseada nesse conceito, bitcoin está desenhada em
torno da ideia de uma nova forma de dinheiro que
usa criptografia para controlar sua criação e as
transações, ao invés de ter que depender de
autoridades centrais.”

4. “Bitcoin: A Peer-to-Peer Electronic
Cash System”
(2008)
• “Uma versão puramente peer-to-peer de dinheiro
eletrônico permitiria que pagamentos online fossem
enviados diretamente de uma parte a outra sem
passar por uma instituição financeira.
• Assinaturas digitais propiciam parte da solução, mas
os principais benefícios são perdidos se uma terceira
parte confiável ainda for necessária para evitar o
duplo-gasto.
• Propomos uma solução ao problema do duplo-gasto
usando uma rede peer-to-peer.”

5. “À medida que a era digital estava no seu
alvorecer no final dos anos 1970’s, uma
enorme pedra no caminho à troca de
informações e à condução de
transações via redes de alta-velocidade
era a falta de segurança de
participantes externos que poderiam
querer interceptar os dados…”
(Resenha de Crypto (Steven Levy, 2000), por
Publishers Weekly.)

6. Steven Levy
(Chief Tech writer, Newsweek)

8. 30 Years of Public-Key Cryptography
(Computer History Museum, Oct 2006)
“Com a possível exceção de armas
nucleares, não consigo pensar em
nenhuma technologia que tenha tido
um impacto político e econômico
profundo sobre o mundo maior que a
criptografia. (...)
Geralmente acho que o papel da
criptografia de chave pública que tem
tido um papel fundamental na
internet moderna, é geralmente
subestimada.
Acho que é provavelmente porque ela está
tão rapidamente se tornando parte
invisível do tecido tanto da
comunicação quanto do comércio
modernos. “ (26/10/2006)
MC: John Markoff (NYT Tech columnist)

9. O que é Criptografia?
Tradicionalmente: manter sigilo na comunicação
Alice e Bob conversam enquanto Eve tenta escutar
Alice Bob
Eve

10. Alice envia mensagem a Bob
• Quando Alice deseja enviar uma mensagem
confidencial a Bob:
• Alice cifra a mensagem usando uma senha
• Alice envia a mensagem cifrada pelo canal de
comunicação (que pode ser escutado por Eve)
• Ao receber a mensagem cifrada:
• Bob decifra a mensagem usando a mesma senha
• Bob recupera a mensagem original em formato puro

11. Sigilo deve se resumir à
chave/senha
“Não se deve supor que o
método de cifragem (e
decifragem) é secreto. É
preciso admitir a
possibilidade de que tais
métodos caiam nas mãos do
adversário, e ainda assim o
sigilo da comunicação seja
mantido.”
Conseqüência: segurança por
obscuridade de métodos é
perigoso. (Ex.: GSM)
Auguste Kerckhoffs (1835–1903)

12. Abordagem Matemática à
Teoria da Informação
• Claude Shannon (1916–
2001).
• A Mathematical Theory of
Communication. Bell
Systems Technical Journal
27:379–423, 623–656, 1948.
• Communication Theory of
Secrecy Systems. Bell Systems
Technical Journal 28:656–
715, 1949.

13. Sigilo Perfeito
Um esquema criptográfico é perfeitamente sigiloso se:
1. a senha tem o mesmo tamanho da mensagem
2. a cada mensagem uma senha é sorteada

14. Tempos Modernos
• Até os anos 70’s – sobretudo área militar e
confidencial
• Desde então - crescimento explosivo
– Aplicações comerciais
– Trabalho científico: relacionamento estreito com Teoria da
Complexidade Computacional
– Destaques: Diffie-Hellman, Rivest-Shamir-Adleman
• Recentemente – modelos mais sofisticados para
tarefas as mais diversas
Como manter o sigilo, a integridade e a autenticidade
em sistemas de informação e comunicação

15. Merkle Hellman Diffie
“Estamos hoje à beira de uma revolução em criptografia.”
(New Directions in Cryptography, 1976)

16. Whitfield Diffie Martin Hellman
Troca de Chaves
Assinaturas Digitais

17. Primórdios da Noção de
“Chave Pública”
1974: “Conforme as concepções
tradicionais da segurança
criptográfica, é necessário
transmitir uma chave, por
meio secreto, antes que
mensagens cifradas possam
ser enviadas de forma segura.
Este artigo mostra que é possível
selecionar uma chave sobre
canais abertos de
comunicação de tal forma
que a segurança das
communicações possa ser
mantida.”
Ralph Merkle

18. Projeto rejeitado: “sua descrição está terrivelmente confusa”

19. Bob
Alice
Chaves Públicas
Chave/Senha Pública

20. Fragilidade
• Necessidade de “Certificado”
• Suscetível ao ataque “homem-no-meio”
• Tentativas de solução:
• Encriptação baseada na Identidade (Shamir 1984)
• Criptografia de Chave Pública Sem-Certificado (Al-Riyami
& Paterson 2003)

21. Criptografia Moderna e
Complexidade Computacional
Teoria da Complexidade -
• Estuda os recursos necessários
para se resolver problemas
computacionais
• tempo, memória
• Identifica problemas que são
infactíveis de computar.
Criptografia Moderna-
• Encontra maneiras de especificar
requisitos de segurança de
sistemas
• Usa a infactibilidade de
problemas de forma a obter
segurança.
Essas duas áreas estão intimamente ligadas!

22. Funcionalidades da
Criptografia Moderna
• Sigilo
• Autenticação
• Integridade
• Cooperação sem perder a privacidade (ex. leilão
eletrônico; estatísticas conjuntas entre concorrentes;
pesquisas de opinião; votação eletrônica; etc.)

23. Encriptação Totalmente
Homomorfa
• Encriptação homomorfa é uma forma de
encriptação na qual uma operação algébrica
específica realizada no purotexto é equivalente a
uma outra operação algébrica (possivelmente
diferente) realizada no cifrotexto.

24. Aplicação
• Em 2010 Riggio & Sicari apresentaram uma
aplicação prática da encriptação homomorfa a uma
rede de sensores sem-fio híbrida.
• O sistema permite monitoramento sem fio
multiponto transparente que é capaz de realizar
análise estatística de vários tipos de dados
(temperatura, humidade, etc.) vindos de uma WSN
enquanto que garante tanto a encriptação fim–a–fim
quanto a autenticação ponto-a-ponto.

25. Especificação Rigorosa de
Segurança
Para definir segurança de um sistema é preciso especificar:
1. O que constitui uma falha do sistema
2. O poder do adversário
• capacidade computacional
• acesso ao sistema
• definição precisa do que significa “quebrar” o sistema.

26. Funções e suas inversas
Dizemos que uma função f é difícil de
inverter se, dado y=f(x) é difícil
encontrar x’ tal que y=f(x’)
– x’ não precisa ser igual a x
– Exemplos: (1) multiplicação; (2) exponenciação
• Para dizer o que é “difícil” temos que
especificar um modelo computacional

27. Modelo Computacional:
“Máquina de Turing”
Alan Turing.
“On computable
numbers, with an
application to the
Entscheidungsproblem”
, Proc. London
Mathematical Society,
Series 2,
42(1936-1937), pp.
230-265

28. Início da Criptografia Moderna
Whitfield Diffie & Martin Hellman (1976)
• Alice e Bob compartilham um primo p, a base g, e querem estabelecer
uma chave (senha)
1. Alice calcula A = ga mod p, e envia A para Bob
2. Bob calcula B = gb mod p, e envia B para Alice
3. Alice calcula KA = Ba mod p
4. Bob calcula KB = Ab mod p
– KA = Ba mod p = gba mod p = gab mod p = Ab mod p = KB
• Abelhudo só consegue aprender p, g, A e B – e é difícil calcular K
somente a partir desses valores (problema do logaritmo discreto)
• Resultado: Estabelecimento seguro de chave (senha) usando somente
troca pública de informação

30. 1973: Cocks realizou idéia de Ellis
(1970): encriptação “não-secreta”

31. Rivest, Shamir & Adleman

32. RSA: artigo original: relatório
técnico circulado em 1977

33. Fatoração em Tempo
Polinomial• “Em um computador quântico, fatorar um inteiro N, o algoritmo
de Peter Shor (1994) roda em tempo polinomial (em log N, que é
o tamanho da entrada).
• Especificamente, O((log N)3), o que mostra que o problema da
fatoração pode ser eficientemente resolvido em um computador
quântico e está portanto na classe de complexidade BQP.
• Isso é exponencialmente mais rápido que o algoritmo clássico
mais eficiente que se conhece, to crivo de número de campo
geral, que roda em tempo sub-exponencial —O(e1.9 (log N)1/3 (log log
N)2/3).
• A eficiência se deve ao poder da transformada de Fourier
quântica, e da exponenciação modular por elevação ao
quadrado”. (Wikipédia)

34. Outros Problemas
Computacionalmente Difíceis
• Problemas sobre
reticulados: por exemplo,
encontrar o vetor mais curto
• Problemas sobre códigos
• Problemas NP-Difíceis

35. Dave Bacon (2003)
• “Demonstramos que um computador quântico que
tenha acesso a “curva temporal fechada” qubits pode
resolver problemas NP-completos com apenas um
número polinomial de portas quânticas.”
(Physical Review A, 2004)

36. Objetivos da
“Criptografia Pós-Quântica”
• Desenvolver criptossistemas baseados em problemas
demonstravelmente intratáveis (pelo menos em
computadores quânticos).
• Avaliar a segurança e a usabilidade na prática.
• Quantificar a complexidade quântica das hipóteses
de intratabilidade.

37. Problemas Computacionais
• P: solúveis em tempo polinomial determinístico.
• NP: solúveis em tempo polinomial não-
determinístico (ou checáveis em tempo polinomial).
• PSPACE: solúveis em espaço polinomial.
• BQP: solúveis por um computador quântico em
tempo polinomial, com uma probabilidade de erro
de no máximo 1/3 para todas as instâncias. (Trata-se
do análogo quântico da classe de complexidade
BPP.)

38. Relação entre Classes de
Complexidade
Sabe-se que
• P ⊆ NP ⊆ PSPACE
• P ⊆ NP ⊆ BQP
• BPP ⊆ BQP

39. Criptossistemas Mais
Utilizados
• Fatoração Inteira –IFP: RSA.
• Logaritmo Discreto e Problema de Diffie-Hellman –
DLP, CDHP, DDHP, BDHP, …: (EC)DSA,
(EC)DH, criptossistemas baseados em
emparelhamentos (curvas elípticas).
• Tais hipóteses de intratabilidade (e várias outras) se
reduzem à intratabilidade do “Problema do
Subgrupo Escondido”(Hidden Subgroup Problem–
HSP).

40. Problema do Subgrupo
Escondido
Seja G um grupo, H ≤ G, e f uma função sobre G. Dizemos que f
separa co-conjuntos H se f(u) = f(v) ⇔ uH = vH, ∀u, v∈G.
• Problema do Subgrupo Escondido (HSP):
• Seja A um oráculo para computar uma função que separa co-
conjuntos de um subgrupo H ⊂ G. Encontre um conjunto
gerador para H usando a informação obtida de A.
Casos especiais importantes:
• Hidden Abelian Subgroup Problem (HASP)
• Hidden Dihedral Subgroup Problem (HDSP)

41. Computação Quântica
• Algoritmos quânticos podem resolver casos
particulares do problema HASP (incluindo
Fatoração e Logaritmo Discreto) em tempo
polinomial aleatório (i.e., classe de complexidade
R).

42. Soluções de Segurança
Criptográfica
Criptografia puramente quântica:
• Quais esquemas estão disponíveis?
• Migração?
Alternativas clássicas:
• Se BQP⊂NP, então sistemas baseados em
problemas que não pertencem a BQP (“post-
quantum”).

43. Criptossistemas Pós-Quânticos
• Grupos Não-Abelianos
• Equivalentes (sobretudo baseados em conjugação) de esquemas DL
sobre grupos de tranças, grupos hiperbólicos, …
• Redução de Reticulados
• Ajtai-Dwork, GGH, LWE, NTRU, ...
• Teoria dos Códigos
• McEliece, Niederreiter, CFS, ...
• Assinaturas de Merkle
• Outros sistemas:
• Núcleos Permutados e Perceptrons, Sistemas Quadráticos
Multivariados, Equações Lineares com Restrições...

44. E se NP⊂BQP?
• Mesmo se P= NP, problemas NP-difíceis que não
pertencem a NP poderiam permanecer intratáveis.
• Em todo caso, poderia haver problemas
teoricamente infactíveis (estritamente exponenciais)
que sejam tratáveis na prática.
• Se nada der certo, tente usar problemas de decisão
não-recursivos, tornando os criptossistemas seguros
contra atacantes computacionalmente ilimitados!
(Myasnikov-Shpilrain-Ushakov2006)

45. Criptografia e Segurança
Criptografia
• é
• uma tremenda ferramenta
• a base para muitos mecanismos de segurança
• não é
• a solução para todos os problemas de segurança
• confiável a menos que implementada corretamente
• confiável a menos que usada corretamente

46. Má Implementação
“Here Come The + Ninjas”
Thai Duong Juliano Rizzo
May 13, 2011
Abstract
Este artigo introduz um ataque rápido bloco-a-bloco de purotexto-
escolhido contra SSL 3.0 e TLS 1.0. Também descrevemos
uma aplicação do ataque que permite um atacante decriptar
eficientemente e obter tokens de autenticação embutidos em
solicitações HTTPS. Os exploits resultantes funcionam nos
principais web browsers no momento em que escrevemos o
artigo.