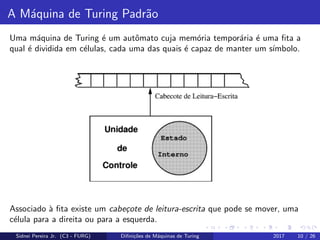
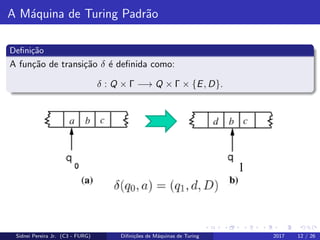
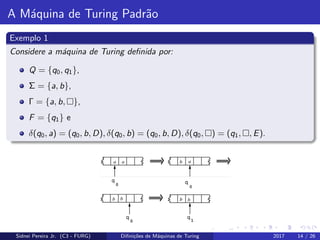
Este documento apresenta conceitos fundamentais sobre linguagens formais, gramáticas e autômatos, e define a máquina de Turing padrão. O documento discute noções como alfabetos, cadeias, linguagens e operações em linguagens. Em seguida, introduz o modelo de máquina de Turing, definindo-o formalmente e apresentando exemplos ilustrativos.

1. Linguagens Formais e Teoria da Computa¸c˜ao
Sidnei Pereira Jr.
Universidade Federal do Rio Grande
sidnei.pereira@furg.br
2017
Sidnei Pereira Jr. (C3 - FURG) Difini¸c˜oes de M´aquinas de Turing 2017 1 / 26

2. Agenda
1 Introdu¸c˜ao
No¸c˜oes de Linguagens, Gram´aticas e Autˆomatos
2 A M´aquina de Turing Padr˜ao
Defini¸c˜ao de M´aquina de Turing
3 M´aquinas de Turing como Reconhecedoras de Linguagens
Sidnei Pereira Jr. (C3 - FURG) Difini¸c˜oes de M´aquinas de Turing 2017 2 / 26

3. No¸c˜oes de Linguagens, Gram´aticas e Autˆomatos
Linguagens naturais
Portuguˆes, inglˆes...
Linguagens formais
Todas as regras da linguagem s˜ao explicitamente declaradas
N˜ao permite viola¸c˜ao `as regras
Linguagens de programa¸c˜ao: Compiladores
Abstratas
Sidnei Pereira Jr. (C3 - FURG) Difini¸c˜oes de M´aquinas de Turing 2017 3 / 26

4. No¸c˜oes de Linguagens, Gram´aticas e Autˆomatos
Alfabeto
Conjunto de s´ımbolos representado por Σ
Cadeias ou strings
Sequˆencias finitas de s´ımbolos: se o alfabeto for Σ = {a, b}, ent˜ao a abab
e aaabba s˜ao cadeias sobre Σ. a cadeia vazia ´e aquela sem nenhum
s´ımbolo, e ser´a denotada por λ
Concaten¸c˜ao
Jun¸c˜ao de palavras: sejam w = bbab e v = aaab. Ent˜ao wv = bbabaaab
e vw = aaabbbab
Palavra reversa
S´ımbolos na ordem contr´aria: sejam w = bbab e v = aaab. Ent˜ao
wR = babb e vR = baaa
Sidnei Pereira Jr. (C3 - FURG) Difini¸c˜oes de M´aquinas de Turing 2017 4 / 26

5. No¸c˜oes de Linguagens, Gram´aticas e Autˆomatos
Prefixo e Sufixo
Se w = vu. Ent˜ao v ´e chamado de prefixo e u ´e chamado de sufixo de w. Seja
w = abbab, o conjunto de todos os prefixos de w ´e {λ, a, ab, abb, abba, abbab} e
de todos os sufixos ´e {λ, b, ab, bab, bbab, abbab}
Comprimento
Denotado por |w|, ´e o n´umero de simbolos: wn ´e a cadeia obtida
concatenando w com ela pr´opria n vezes. Portanto, wn+1 = wwn. No
caso especial de n = 0, w0 = λ.
Fecho Estrela e Fecho Positivo
O fecho estrela Σ∗
, ´e o conjunto de todas as cadeias (finitas) obtidas
concatenando zero ou mais s´ımbolos de Σ. O fecho positivo Σ+
, ´e o conjunto de
todas as cadeias (finitas) de Σ sem a cadeia vazia. Isto ´e, Σ+
= Σ∗
− {λ}. Se
Σ = {a}, ent˜ao Σ∗
= {λ, a, aa, aaa, aaaa, . . .}
Sidnei Pereira Jr. (C3 - FURG) Difini¸c˜oes de M´aquinas de Turing 2017 5 / 26

6. No¸c˜oes de Linguagens, Gram´aticas e Autˆomatos
Linguagens
Um subconjunto qualquer de Σ∗ pode ser visto como um linguagem sobre
o alfabeto Σ. Uma cadeia w numa linguagem L, isto ´e w ∈ L, ser´a
chamada palavra ou senten¸ca.
Exemplo
Seja Σ = {a, b}. Ent˜ao Σ∗ = {λ, a, b, aa, ab, ba, bb, aaa, aab, ...}. O
conjunto L = {a, aa, aab}, uma linguagem finita, e L = {anbn|n ≥ 0},
uma linguagem infinita, s˜ao linguagens sobre Σ.
Sidnei Pereira Jr. (C3 - FURG) Difini¸c˜oes de M´aquinas de Turing 2017 6 / 26

7. No¸c˜oes de Linguagens, Gram´aticas e Autˆomatos
Defini¸c˜ao
Como as linguagens s˜ao conjuntos: opera¸c˜oes de uni˜ao, interse¸c˜ao e diferen¸ca de
duas linguagens s˜ao imediatamente definidadas. O complemento de uma
linguagem L sobre um alfabeto Σ, ´e definida com respeito a Σ∗
, isto ´e, o
complemento de L ´e a linguagem, sobre Σ, definida por L = Σ∗
− L.
Complemento
Seja L = {w ∈ Σ∗||w| ´e par}. Ent˜ao L = {w ∈ Σ∗||w| ´e ´ımpar}
Concatena¸c˜ao
Seja L = {anbn|n ≥ 0}. Ent˜ao L2 = {ambmanbn|m ≥ 0 e n ≥ 0}
Sidnei Pereira Jr. (C3 - FURG) Difini¸c˜oes de M´aquinas de Turing 2017 7 / 26

8. No¸c˜oes de Linguagens, Gram´aticas e Autˆomatos
Fecho Estrela e Fecho Positivo
Seja L = {aa, bb, aba}, ent˜ao
L∗
= {λ, aa, bb, aba, aaaa, aabb, aaaba, bbaa, bbbb, bbaba, abaaa, ababb, abaaba, aaaaaa, ...}, e
L+
= {aa, bb, aba, aaaa, aabb, aaaba, bbaa, bbbb, bbaba, abaaa, ababb, abaaba, aaaaaa, ...}
Reversa
w ∈ L se e somente se wR
∈ LR
. Como (wR
)R
= w para qualquer cadeia w,
definimos LR
= {w ∈ |wR
∈ L}. Seja L = {aa, baa, aba, abbb}, ent˜ao
LR
= {aa, aab, aba, bbba}
Prefixo e Sufixo
LP
= {v ∈ Σ∗
|vw ∈ L para algum w ∈ Σ∗
}. E LS
= {w ∈ Σ∗
|vw ∈ L para algum
v ∈ Σ∗
}. Seja L = {aa, ba, baa}, ent˜ao LP
= {λ, a, b, aa, ba, baa} e
LS
= {λ, a, ba, aa, baa}
Sidnei Pereira Jr. (C3 - FURG) Difini¸c˜oes de M´aquinas de Turing 2017 8 / 26

9. No¸c˜oes de Linguagens, Gram´aticas e Autˆomatos
Linguagens Regulares
1 Autˆomatos Finitos
2 Gram´aticas Regulares
3 Example
Linguagens livres de contexto
1 Autˆomatos de Pilha
2 Gram´aticas Livres de Contexto
3 Example
As linguagens regulares s˜ao subconjunto pr´oprio das linguagens livres do
contexto.
Mas, e linguagens simples do tipo:
L = {anbncn|n ≥ 0} e {ww|w ∈ {a, b}}.
N˜ao s˜ao livres do contexto.
Sidnei Pereira Jr. (C3 - FURG) Difini¸c˜oes de M´aquinas de Turing 2017 9 / 26

10. A M´aquina de Turing Padr˜ao
Uma m´aquina de Turing ´e um autˆomato cuja mem´oria tempor´aria ´e uma fita a
qual ´e dividida em c´elulas, cada uma das quais ´e capaz de manter um s´ımbolo.
Associado `a fita existe um cabe¸cote de leitura-escrita que pode se mover, uma
c´elula para a direita ou para a esquerda.
Sidnei Pereira Jr. (C3 - FURG) Difini¸c˜oes de M´aquinas de Turing 2017 10 / 26

11. A M´aquina de Turing Padr˜ao
Defini¸c˜ao 8.1.1
Uma m´aquina de Turing M ´e uma s´ete-tupla M = Q, Σ, Γ, δ, q0, , F , onde
Q ´e um conjunto finito de estados interno,
Σ ´e um conjunto finito de s´ımbolos, chamado alfabeto de entrada,
Γ ´e um conjunto finito de s´ımbolos, chamado alfabeto da fita,
δ ´e uma fun¸c˜ao (parcial) de transi¸c˜oes,
∈ Γ ´e um s´ımbolo especial, chamado branco,
q0 ∈ Q ´e o estado inicial e
F ⊆ Q ´e o conjunto de estados finais.
Na defini¸c˜ao, assumiremos que Σ ⊆ Γ − , isto ´e, que o alfabeto de entrada, n˜ao
inclui o branco.
Sidnei Pereira Jr. (C3 - FURG) Difini¸c˜oes de M´aquinas de Turing 2017 11 / 26

12. A M´aquina de Turing Padr˜ao
Defini¸c˜ao
A fun¸c˜ao de transi¸c˜ao δ ´e definida como:
δ : Q × Γ −→ Q × Γ × {E, D}.
Sidnei Pereira Jr. (C3 - FURG) Difini¸c˜oes de M´aquinas de Turing 2017 12 / 26

13. A M´aquina de Turing Padr˜ao
Defini¸c˜ao
Podemos ver uma m´aquina de Turing como um computador simples: unidade de
processamento, com mem´oria finita e a fita, unidade de mem´oria secund´aria com
capacidade ilimitada.
Instru¸c˜oes
perceber um s´ımbolo na fita;
us´a-lo como resultado para
decidir o pr´oximo passo.
A¸c˜oes
rescrever o s´ımbolo corrente;
trocar o estado do controle e mover
o cabe¸cote uma c´elula, para direita
ou esquerda.
Defini¸c˜ao
Uma m´aquina de Turing p´ara de computar se atinge uma configura¸c˜ao para a
qual δ n˜ao est´a definida. Isto ´e poss´ıvel porque δ ´e uma fun¸c˜ao parcial. De fato,
assumiremos que s´o existe um ´unico estado final para o qual n˜ao s˜ao definidas
transi¸c˜oes. Portanto, a m´aquina de Turing parar´a sempre que ela entrar nesse
estado final.
Sidnei Pereira Jr. (C3 - FURG) Difini¸c˜oes de M´aquinas de Turing 2017 13 / 26

14. A M´aquina de Turing Padr˜ao
Exemplo 1
Considere a m´aquina de Turing definida por:
Q = {q0, q1},
Σ = {a, b},
Γ = {a, b, },
F = {q1} e
δ(q0, a) = (q0, b, D), δ(q0, b) = (q0, b, D), δ(q0, ) = (q1, , E).
Sidnei Pereira Jr. (C3 - FURG) Difini¸c˜oes de M´aquinas de Turing 2017 14 / 26

15. A M´aquina de Turing Padr˜ao
Exemplo 2
Tome Q, Σ, Γ e F, como no exemplo anterior. Defina δ por:
δ(q0, a) = (q1, a, D), δ(q0, b) = (q1, b, D), δ(q0, ) = (q1, , D),
δ(q1, a) = (q0, a, E), δ(q1, b) = (q0, b, E), δ(q1, ) = (q0, , D).
Sidnei Pereira Jr. (C3 - FURG) Difini¸c˜oes de M´aquinas de Turing 2017 15 / 26

16. A M´aquina de Turing Padr˜ao
Caracter´ısticas do Modelo
1 A m´aquina de Turing tem uma fita que ´e ilimitada em ambas as dire¸c˜oes,
permitindo qualquer n´umero de movimentos para a direita ou para a
esquerda.
2 A m´aquina de Turing ´e determin´ıstica no sentido de que δ define, no
m´aximo, um movimento para cada configura¸c˜ao.
3 N˜ao existe fita de entrada especial. Assumimos que no in´ıcio a fita tem um
conte´udo especial. Alguns destes podem ser considerados entradas.
Analogamente, n˜ao existe nenhum dispositivo de sa´ıda. Sempre que a
m´aquina p´ara, algum, ou todo o conte´udo da fita pode ser visto como sa´ıda.
Descri¸c˜ao Instantˆanea
Qualquer configura¸c˜ao de uma m´aquina de Turing ´e completamente determinada
pelo estado corrente da unidade de controle, o conte´udo da fita, e a posi¸c˜ao do
cabe¸cote de leitura-escrita.
Sidnei Pereira Jr. (C3 - FURG) Difini¸c˜oes de M´aquinas de Turing 2017 16 / 26

17. A M´aquina de Turing Padr˜ao
Defini¸c˜ao
Seja M = Q, Σ, Γ, δ, q0, , F uma m´aquina de Turing. Toda tripla
(u, q, v) ∈ Γ × Q × Γ ´e chamada de descri¸c˜ao instantˆanea de M. Por
simplicidade notacional escreveremos uqv em vez de (u, q, v).
a1a2 · · · ak−1qakak+1 · · · an
Exemplo 3
A sequˆencia de descri¸c˜ao instantˆanea do Exemplo 1 ´e q0aa, bq0a, bbq0 e bbq1b.
Sidnei Pereira Jr. (C3 - FURG) Difini¸c˜oes de M´aquinas de Turing 2017 17 / 26

18. A M´aquina de Turing Padr˜ao
Defini¸c˜ao
Um movimento v´alido de uma configura¸c˜ao a outra ser´a denotado por .
Portanto, se
δ(q1, c) = (q2, e, D)
um movimento poss´ıvel ´e
abq1cd abeq2d.
Os simbolos ∗
e +
podem ser usados para representar um n´umero arbrit´ario de
movimentos.
Exemplo 4
A a¸c˜ao da m´aquina de Turing do Exemplo 1 pode ser representada por
q0aa bq0a bbq0 bq1b. ou q0bb ∗
bq1b.
Sidnei Pereira Jr. (C3 - FURG) Difini¸c˜oes de M´aquinas de Turing 2017 18 / 26

19. A M´aquina de Turing Padr˜ao
Defini¸c˜ao 8.1.8
Sejam u, v ∈ Γ∗
, a, b, c ∈ Γ e q, q ∈ Q. Se δ(q, a) = (q , b, D) ent˜ao h´a um
movimento v´alido da descri¸c˜ao instantˆanea uqav para a descri¸c˜ao instantˆanea
ubq v que denotamos por uqav ubq v. Se δ(q, a) = (q , b, E) ent˜ao h´a um
movimento v´alido da descri¸c˜ao instantˆanea ucqav para a descri¸c˜ao instantˆanea
uq cbv que denotamos por ucqav uq cbv.
Defini¸c˜ao 8.1.8
Uma descri¸c˜ao instantˆanea uqpav ´e uma configura¸c˜ao de parada, denotado por
uqpav ⊥, se δ(qp, a) n˜ao ´e definido ou, equivalente, se n˜ao existe uma descri¸c˜ao
instantˆanea u q v tal que uqpav u q v . Assim, uma m´aquina de Turing M
p´ara para a descri¸c˜ao instantˆanea inicial uqv se
uqv ∗
⊥.
A sequˆencia de configura¸c˜ao levando a uma configura¸c˜ao de para em que o
estado ser´a chamda de computa¸c˜ao
Sidnei Pereira Jr. (C3 - FURG) Difini¸c˜oes de M´aquinas de Turing 2017 19 / 26

20. A M´aquina de Turing Padr˜ao
Sidnei Pereira Jr. (C3 - FURG) Difini¸c˜oes de M´aquinas de Turing 2017 20 / 26

21. A M´aquina de Turing Padr˜ao
Defini¸c˜ao 8.1.7 (2009)
O exemplo 8.1.4 mostra a possibilidade de que uma m´aquina de Turing pode
nunca parar, permanecendo em um la¸co sem fim do qual ela n˜ao pode escapar.
Esta situa¸c˜ao desempenha um papel fundamental de uma m´aquina de Turing,
representemo-la por
uqv ∗
∞ ou x1qx2
∗
∞ .
indicando que, iniciando da configura¸c˜ao inicial uqv a m´aquina nunca p´ara.
Sidnei Pereira Jr. (C3 - FURG) Difini¸c˜oes de M´aquinas de Turing 2017 21 / 26

22. A M´aquina de Turing como Reconhecedora de Linguagens
Sidnei Pereira Jr. (C3 - FURG) Difini¸c˜oes de M´aquinas de Turing 2017 22 / 26

23. A M´aquina de Turing como Reconhecedora de Linguagens
Defini¸c˜ao 8.1.9
Seja M = Q, Σ, Γ, δ, q0, , F uma m´aquina de Turing. Ent˜ao a linguagem
reconhecida por M ´e
L(M) = {w ∈ Σ∗
| q0w ∗
uqf v} para algum qf ∈ F, u, v ∈ Γ∗
Sidnei Pereira Jr. (C3 - FURG) Difini¸c˜oes de M´aquinas de Turing 2017 23 / 26

24. A M´aquina de Turing como Reconhecedora de Linguagens
Sidnei Pereira Jr. (C3 - FURG) Difini¸c˜oes de M´aquinas de Turing 2017 24 / 26

25. References
Aci´oly, Benedito. e Bedregal, Benjam´ın R.C. e Lyra, Aar˜ao (2010)
Introdu¸c˜ao `a Teoria das Linguagens Formais, dos Autˆomatos e da Computabilidade.
Sidnei Pereira Jr. (C3 - FURG) Difini¸c˜oes de M´aquinas de Turing 2017 25 / 26

26. The End
Sidnei Pereira Jr. (C3 - FURG) Difini¸c˜oes de M´aquinas de Turing 2017 26 / 26