O documento discute cinemática de partículas, incluindo movimento retilíneo e curvilíneo. Aborda conceitos como posição, velocidade, aceleração e como determinar o movimento de uma partícula a partir destas grandezas. Apresenta exemplos numéricos de problemas de movimento retilíneo uniforme e uniformemente acelerado.





















![FACULDADE DO CENTRO LESTE www.ucl.br
Julio Rezende Juliorezende@ucl.br
MECÂNICAII-DINÂMICA
Exemplo 5
11 - 27
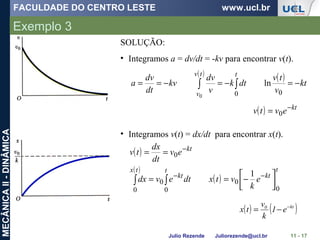
SOLUÇÃO:
• Colocamos a origem na superfície horizontal
superior e escolhemos o sentido positivo para baixo.
• O cursor A tem movimento retilíneo uniformemente
acelerado. Calculamos sua aceleração e o tempo t
para que passe por L.
( ) ( )[ ]
( ) 2
2
0
2
0
2
s
cm
5,22cm202
s
cm
30
2
==
−+=
AA
AAAAA
aa
xxavv
( )
s333,1
s
cm
5,22
s
cm
30 2
0
==
+=
tt
tavv AAA](https://image.slidesharecdn.com/cap11-161008005245/85/Cap-11-27-320.jpg)
![FACULDADE DO CENTRO LESTE www.ucl.br
Julio Rezende Juliorezende@ucl.br
MECÂNICAII-DINÂMICA
Exemplo 5
11 - 28
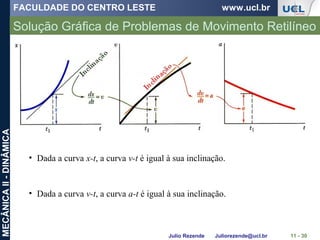
• A polia D tem movimento retilíneo uniforme.
Calculamos a variação da posição no tempo t.
( )
( ) ( ) cm10s333,1
s
cm
5,70
0
=
=−
+=
DD
DDD
xx
tvxx
• O movimento do bloco B é dependente dos movi-
mentos do cursor A e da polia D. Escremos relações
entre os movimentos e as resolvemos para obter a
variação na elevação do bloco B.
O comprimento total do cabo permanece constante,
logo,
( ) ( ) ( )
( )[ ] ( )[ ] ( )[ ]
( ) ( ) ( )[ ] 0cm102cm20
02
22
0
000
000
=−++
=−+−+−
++=++
BB
BBDDAA
BDABDA
xx
xxxxxx
xxxxxx
( ) cm40xx 0BB −=−](https://image.slidesharecdn.com/cap11-161008005245/85/Cap-11-28-320.jpg)

















![FACULDADE DO CENTRO LESTE www.ucl.br
Julio Rezende Juliorezende@ucl.br
MECÂNICAII-DINÂMICA
Exercício
11 - 55
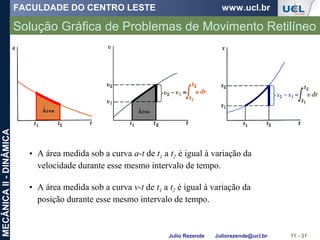
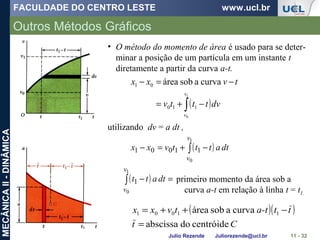
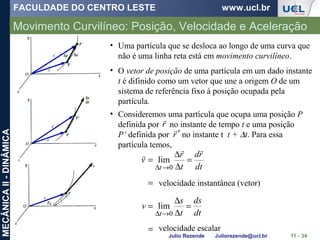
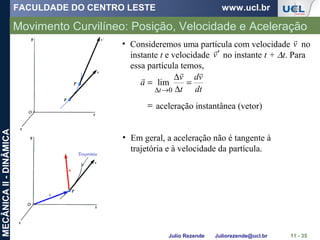
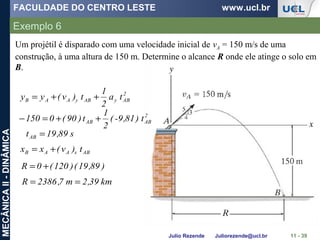
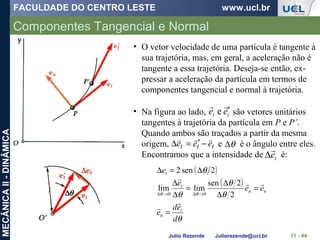
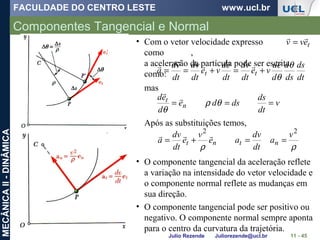
Um barco está se movendo ao longo da trajetória circular de v = (0,0625 t2
)
m/s, onde t é dado em segundos. Determine a intensidade da sua aceleração
quando t = 10 s.
==
dt
dv
at =)t0625,0(
dt
d 2
s10t
)t125,0( =
2
t s/m25,1a =
==
ρ
2
n
v
a =
40
)t0625,0( 22
s10t
46
]t)10(66,97[
=
−
2
n s/m9766,0a =
=+= 2
n
2
t aaa 22
9766,025,1 + 2
s/m59,1a =](https://image.slidesharecdn.com/cap11-161008005245/85/Cap-11-55-320.jpg)


