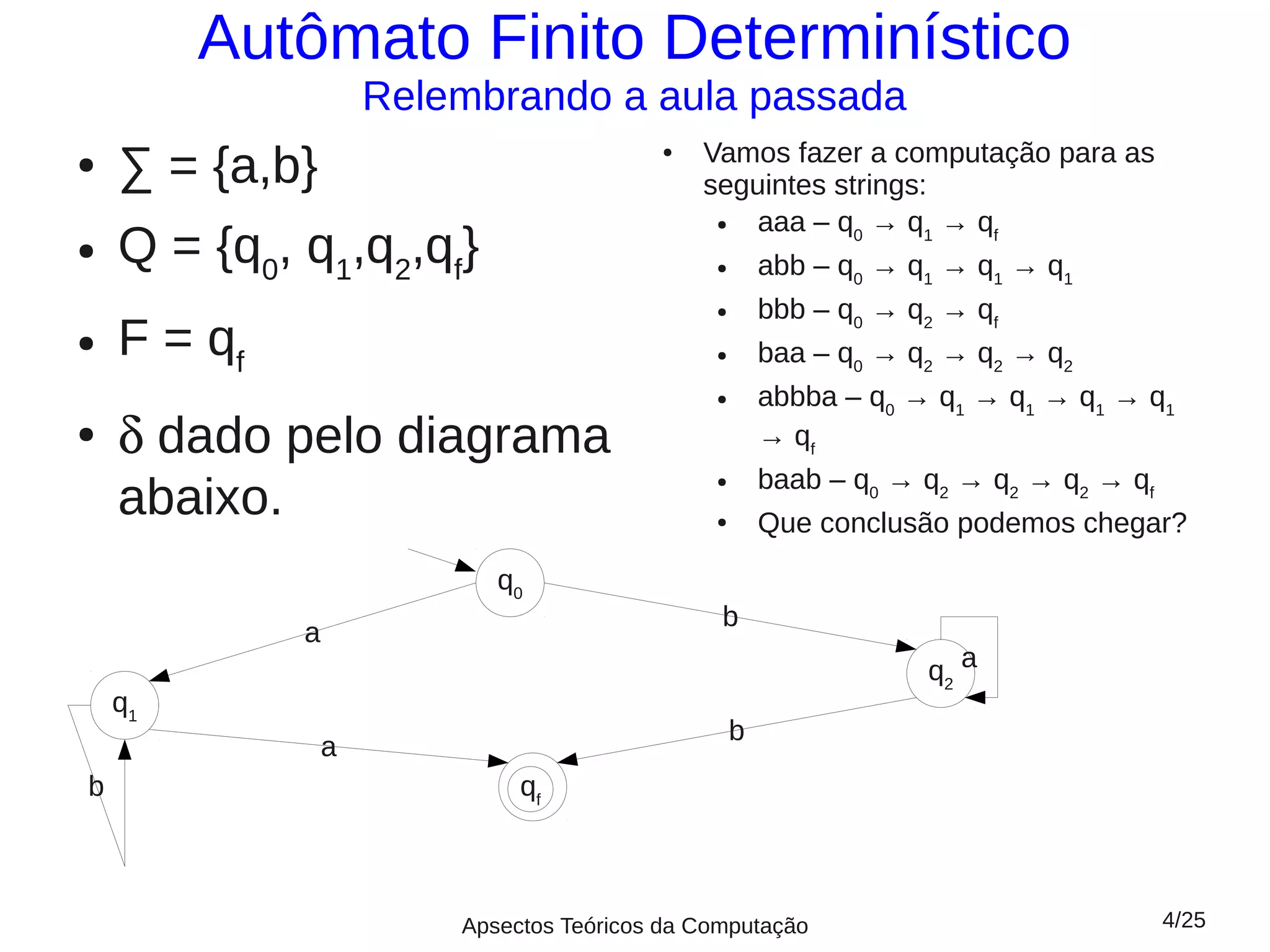
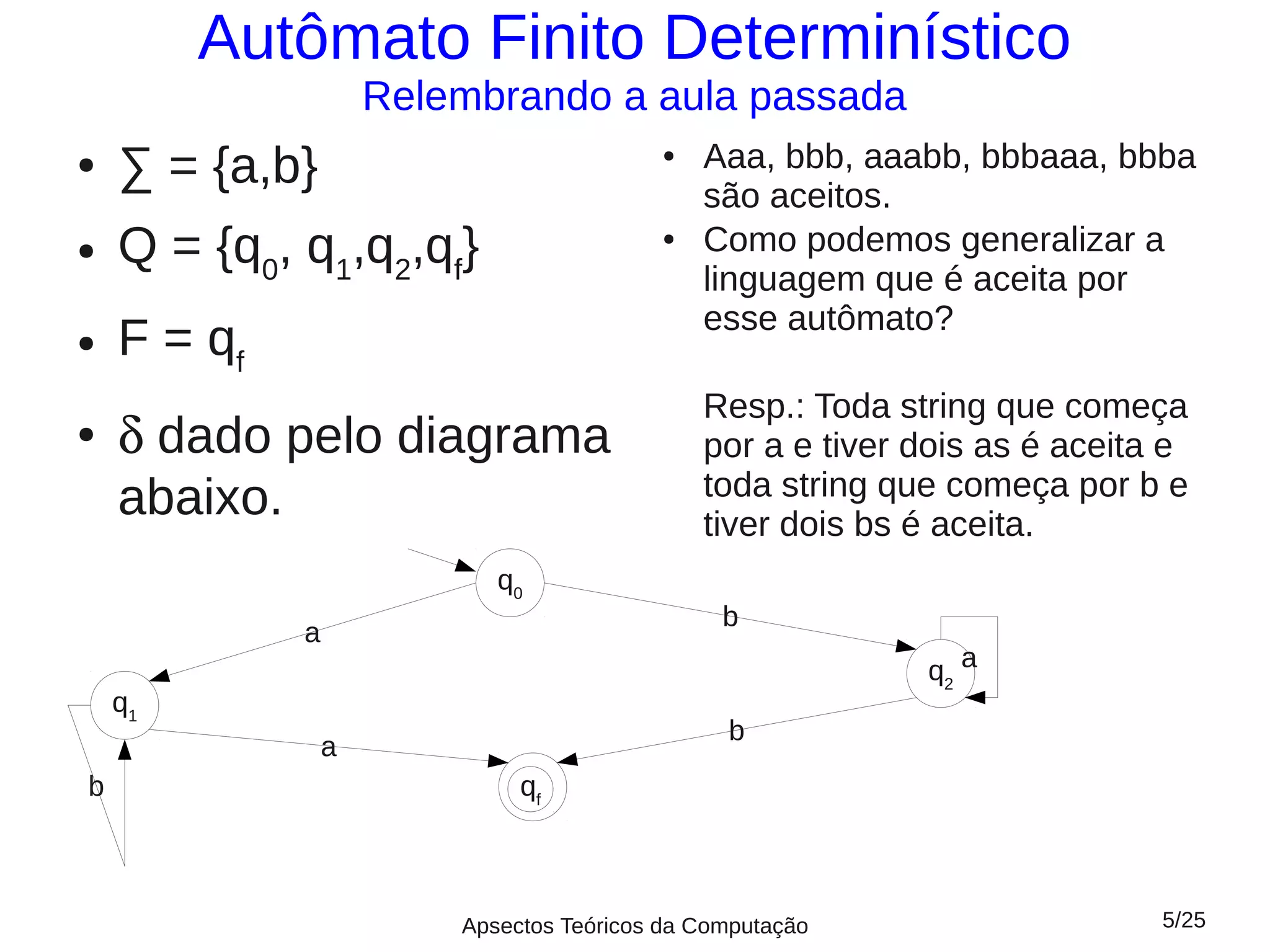
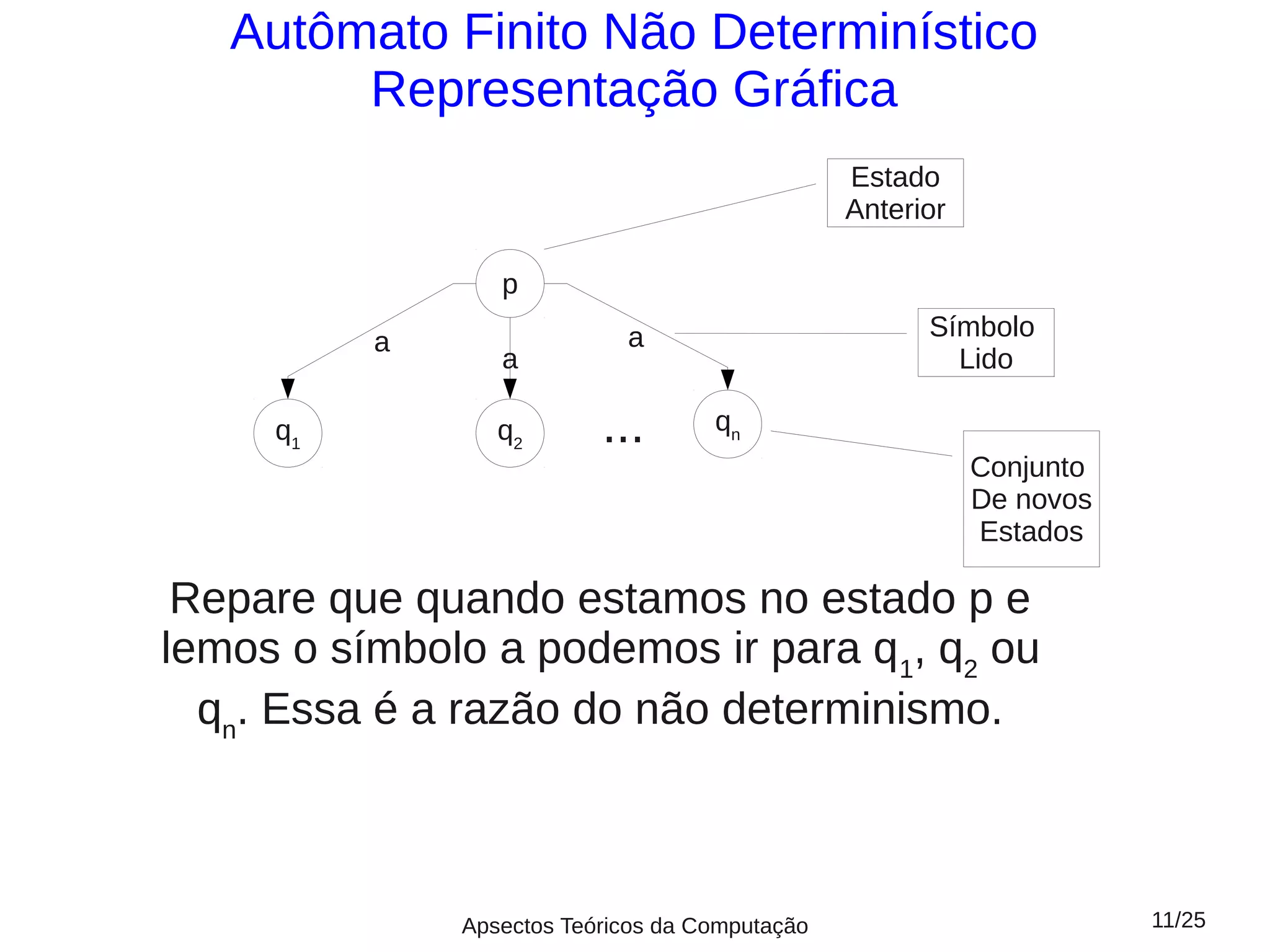
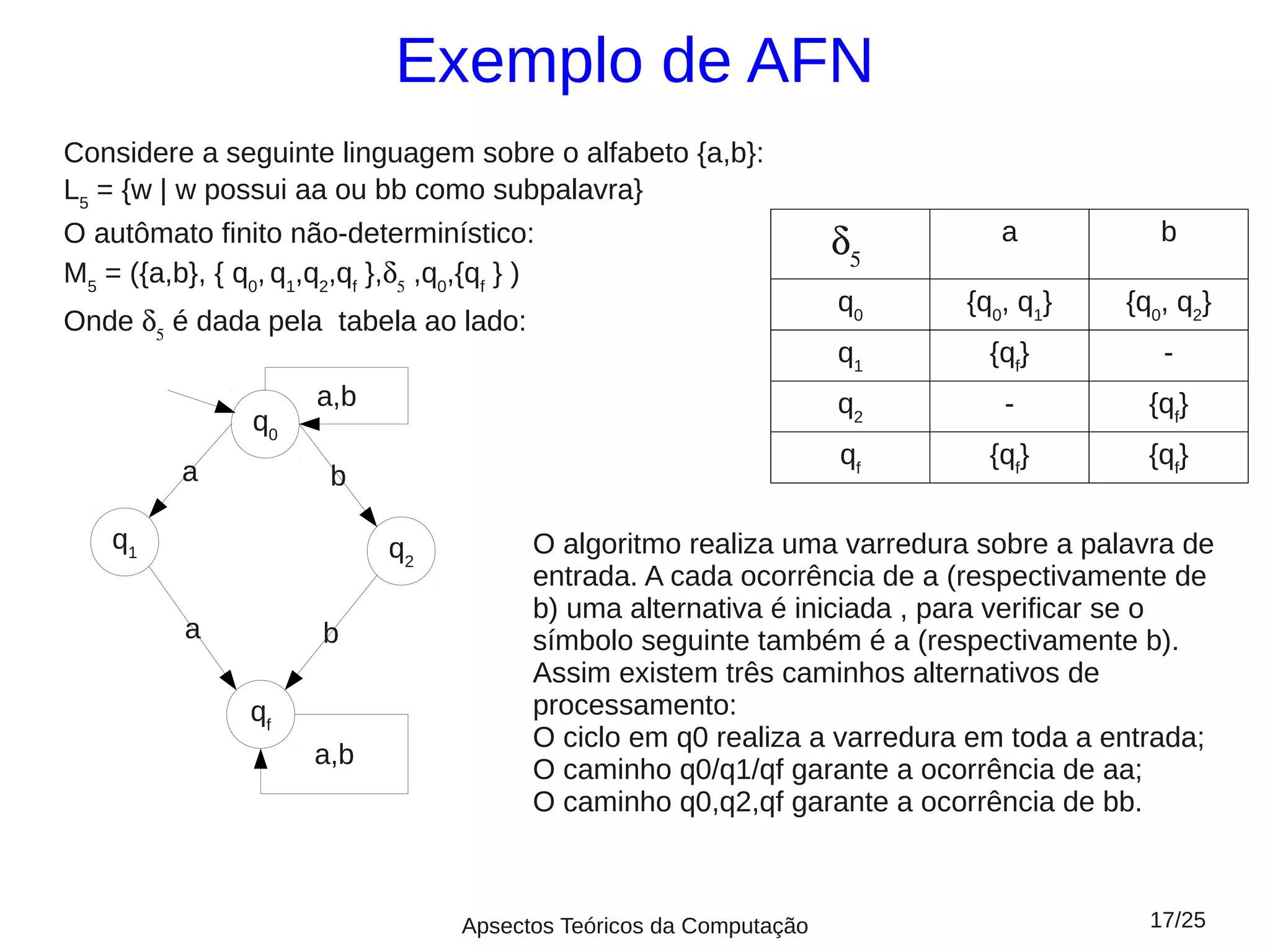
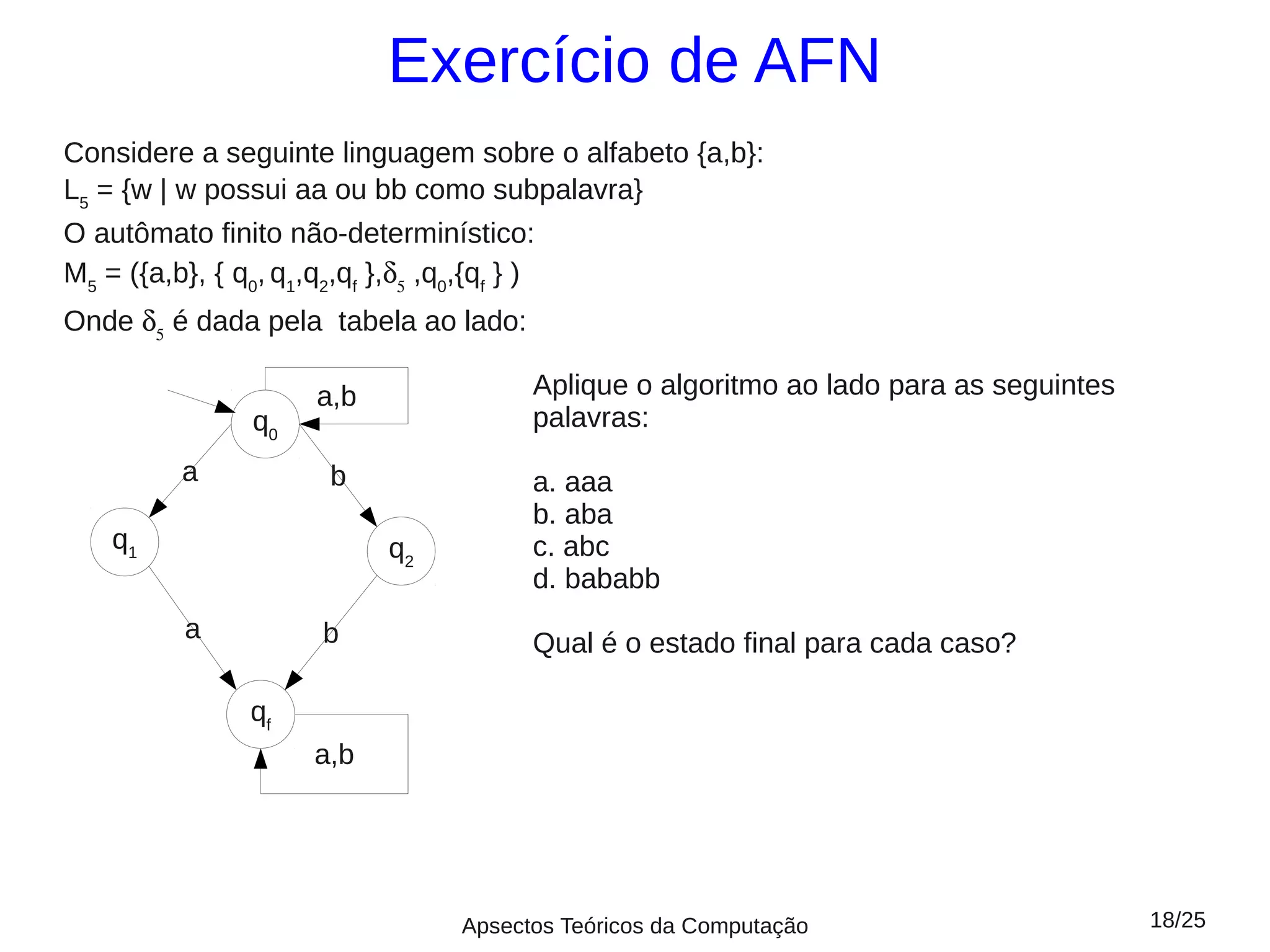
Este documento fornece um resumo da aula 5 sobre linguagens regulares. Apresenta autômatos finitos determinísticos e não determinísticos, definindo suas componentes e como representá-los graficamente. Explica como computar strings usando esses autômatos e define linguagens aceitas e rejeitadas. Dois exemplos ilustram autômatos para linguagens específicas.

1. Curso: Ciência da Computação
Aspectos Teóricos da Computação
Aula 5
Linguagens Regulares
Autômatos Finitos Não Determinísticos

2. Notas de Aula
Blog
https://aspectosteoricosdacomputacao.wordpre
ss.com/
Avaliação dia 8 de Abril.
Apsectos Teóricos da Computação 2/25

3. Linguagens Regulares
● O estudo das linguagens regulares é abordado
usando os seguintes formalismos:
➔ Autômato Finito. Trata-se de um formalismo
operacional ou reconhecedor, sendo basicamente,
um sistema de estados finitos;
➔ Expressão Regular. Trata-se de um formalismo
denotacional, também considerado gerador, o qual
é definido a partir de conjuntos (linguagens)
básicos e das operações de concatenação e de
união;
➔ Gramática Regular. Trata-se de um formalismo
axiomático ou gerador o que, como o nome indica,
é uma gramática, mas com restrições de forma das
regras de produção.
Apsectos Teóricos da Computação 3/25

4. Autômato Finito Determinístico
Relembrando a aula passada
Vamos fazer a computação para as
∑ = {a,b}
●
●
seguintes strings:
aaa – q0 → q1 → qf
Q = {q0, q1,q2,qf}
●
●
● abb – q0 → q1 → q1 → q1
● bbb – q0 → q2 → qf
● F = qf ● baa – q0 → q2 → q2 → q2
● abbba – q0 → q1 → q1 → q1 → q1
● δ dado pelo diagrama → qf
baab – q0 → q2 → q2 → q2 → qf
abaixo.
●
● Que conclusão podemos chegar?
q0
b
a
q2 a
q1
b
a
b qff
Apsectos Teóricos da Computação 4/25

5. Autômato Finito Determinístico
Relembrando a aula passada
● ∑ = {a,b} ● Aaa, bbb, aaabb, bbbaaa, bbba
são aceitos.
● Q = {q0, q1,q2,qf} ● Como podemos generalizar a
linguagem que é aceita por
esse autômato?
● F = qf
Resp.: Toda string que começa
● δ dado pelo diagrama por a e tiver dois as é aceita e
toda string que começa por b e
abaixo. tiver dois bs é aceita.
q0
b
a
q2 a
q1
b
a
b qff
Apsectos Teóricos da Computação 5/25

6. Autômato Finito Não Determinístico
● O não determinismo é uma importante
generalização dos modelos de máquinas,
sendo de fundamental importância no estudo
de modelos para concorrência, Teoria da
Computação e das Linguagens Formais.
● O objetivo é a capacidade de reconhecer
linguagens e de solucionar problemas.
Apsectos Teóricos da Computação 6/25

7. Autômato Finito Não Determinístico
● A facilidade de não determinismo para
autômatos finitos é expressa no programa, que
é uma função parcial tal que:
Dependendo do estado corrente e do símbolo
lido, determina um conjunto de estados do
autômato.
Apsectos Teóricos da Computação 7/25

8. Autômato Finito Não Determinístico
Um Autômato Finito Não Determinístico assume
um conjunto de estados alternativos, como se
houvesse uma multiplicação da unidade de
controle, uma para cada alternativa, processando
independentemente, sem compartilhar recursos
com as demais. Assim, o processamento de um
caminho não influi no estado, símbolo lido e
posição da cabeça dos demais caminhos
alternativos.
Apsectos Teóricos da Computação 8/25

9. Definição: Autômato Finito Não Determinístico
Um Autômato Finito Não Determinístico, abreviado por AFN, é uma 5-upla
ordenada:
M = { ∑, Q, δ, q0, F}
Onde:
a) ∑ é um alfabeto de símbolos de entrada, ou simplesmente, alfabeto de
entrada;
b) Q é o conjunto de estados possíveis do autômato o qual é finito;
c) δ é uma função programa ou função de transição ou simplesmente
programa:
δ : Q x ∑ → 2Q
a qual é uma função parcial. Supondo que a função programa é definida
para um estado p e um símbolo a, resultando no conjunto de estados
{q1,q2,q3,...,qn}, então:
δ(p,a)={q1,q2,q3,...,qn} é uma transição do autômato;
d) Q0 é um elemento distinguido de Q, denominado estado inicial;
e) F é um subconjunto de Q, denominado conjunto de estados finais.
Apsectos Teóricos da Computação 9/25

10. Definição: Autômato Finito Não Determinístico
● Excetuando-se a função programa ou de transição, as componentes ∑, Q,
q0, F são como na definição de autômato finito determinístico.
● A representação da função programa como um diagrama é análoga à do
autômato finito determinístico.
● Assim, a representação diagramática de uma transição do tipo:
δ(p,a)={q1,q2,q3,...,qn}
Resulta em diversas arestas etiquetadas por a, com origem em p, e com
destino em cada estado q1,q2,q3,...,qn .
Apsectos Teóricos da Computação 10/25

11. Autômato Finito Não Determinístico
Representação Gráfica
Estado
Anterior
p
a Símbolo
a
a Lido
q1 q2 ... qn
Conjunto
De novos
Estados
Repare que quando estamos no estado p e
lemos o símbolo a podemos ir para q1, q2 ou
qn. Essa é a razão do não determinismo.
Apsectos Teóricos da Computação 11/25

12. Autômato Finito Não Determinístico
Analogamente ao autômato finito determinístico,
a computação de um AFN, para uma palavra w,
consiste na sucessiva aplicação da função
programa para cada símbolo de w (da esquerda
para a direita) até ocorrer uma condição de
parada. Como cada transição do AFN resulta em
um conjunto de estados, é necessário estender a
definição da função programa, usando como
argumento um conjunto finito de estados e uma
palavra.
Apsectos Teóricos da Computação 12/25

13. Função Programa Estendida, Computação
Seja M = { ∑, Q, δ, q0, F} um AFN. A função
programa estendida ou computação de M,
denotada por:
δ*(P, ε) = P
δ*(P, aw) = δ*(Uq є p δ(q,a),w)
Portanto como já vimos a função programa
estendida consiste na sucessiva aplicação da
função programa a cada símbolo da palavra, a
partir de um conjunto de estados. Observe que se
a entrada for vazia o autômato fica parado nos
estados correntes.
Apsectos Teóricos da Computação 13/25

14. Função Programa Estendida, Computação
A transição estendida a um conjunto de estados é a união dos resultados da
função programa aplicado a cada estado alternativo.
δ*({q1,q2,q3,...,qn}, a) = δ(q1,a) U δ(q2,a) U δ(q3,a) U δ(q4,a)U ... U δ(qn,a)
A parada do processamento de afn para uma entrada w pode ser de duas
maneiras:
a. Aceita a entrada w. Após processar o último símbolo da fita, existe pelo
menos um estado final pertencente ao conjunto de estados alternativos
atingidos;
b. Rejeita a entrada w. São duas possibilidades
* após processar o último símbolo da fita, todos os estados alternativos
atingidos são não finais.
* em algum momento ao longo do processamento de w, a função programa
é indefinida para o argumento.
Apsectos Teóricos da Computação 14/25

15. Linguagem Aceita, Linguagem Rejeitada
Seja M = { ∑, Q, δ, q0, F} um AFN. A Linguagem Aceita ou
Linguagem Rejeitada por M, denotada por:
ACEITA(M) ou L(M)
é o conjunto de todas as palavras pertencentes a ∑* tais que
existe pelo menos um caminho alternativo que aceita a palavra, a
partir de {q0}, ou seja:
● ACEITA(M) = { w | δ*({q0},w) ∩ F ≠ Ø}
Analogamente a Linguagem Rejeitada por M denotada por
REJEITA(M)
é o conjunto de todas as palavras pertencentes a ∑* rejeitadas por
todos os caminhos alternativos de M, a partir de {q0}, ou seja:
●
REJEITA(M) = { w | δ*({q0},w) ∩ F = Ø ou δ*({q0},w) é
indefinida}
Apsectos Teóricos da Computação 15/25

16. Exemplo de AFN
Considere a seguinte linguagem sobre o alfabeto {a,b}:
L5 = {w | w possui aa ou bb como subpalavra}
O autômato finito não-determinístico:
M5 = ({a,b}, { q0, q1,q2,qf },δ5 ,q0,{qf } )
Onde δ5 é dada pela seguinte tabela:
δ5 a b
q0 {q0, q1} {q0, q2}
q1 {qf} -
q2 - {qf}
qf {qf} {qf}
Faça o diagrama desse autômato. 5 minutos.
Apsectos Teóricos da Computação 16/25

17. Exemplo de AFN
Considere a seguinte linguagem sobre o alfabeto {a,b}:
L5 = {w | w possui aa ou bb como subpalavra}
O autômato finito não-determinístico: δ5 a b
M5 = ({a,b}, { q0, q1,q2,qf },δ5 ,q0,{qf } )
q0 {q0, q1} {q0, q2}
Onde δ5 é dada pela tabela ao lado:
q1 {qf} -
a,b q2 - {qf}
q0
qf {qf} {qf}
a b
q1 q2 O algoritmo realiza uma varredura sobre a palavra de
entrada. A cada ocorrência de a (respectivamente de
b) uma alternativa é iniciada , para verificar se o
a b símbolo seguinte também é a (respectivamente b).
Assim existem três caminhos alternativos de
qf processamento:
O ciclo em q0 realiza a varredura em toda a entrada;
a,b
O caminho q0/q1/qf garante a ocorrência de aa;
O caminho q0,q2,qf garante a ocorrência de bb.
Apsectos Teóricos da Computação 17/25

18. Exercício de AFN
Considere a seguinte linguagem sobre o alfabeto {a,b}:
L5 = {w | w possui aa ou bb como subpalavra}
O autômato finito não-determinístico:
M5 = ({a,b}, { q0, q1,q2,qf },δ5 ,q0,{qf } )
Onde δ5 é dada pela tabela ao lado:
a,b Aplique o algoritmo ao lado para as seguintes
q0 palavras:
a b a. aaa
b. aba
q1 q2 c. abc
d. bababb
a b Qual é o estado final para cada caso?
qf
a,b
Apsectos Teóricos da Computação 18/25

19. Exemplo
Considere a seguinte linguagem sobre o alfabeto
{a,b}:
L6 = {w | w possui aaa como sufixo}
O autômato finito não determinístico:
M6 = ({a,b}, { q0, q1,q2,qf },δ6 ,q0,{qf })
É tal que ACEITA(M6) = L6.
q0 a q1 a q2 a qf
a,b
Apsectos Teóricos da Computação 19/25

20. Exemplo
aaa – q0 → q1 → q2 → qf Repare que não existem
arcos para o símbolo b
aab – q0 → q1 → q2 (indef) em q1, q2. Caso algum b
seja lido ai o autômato
fica indefinido e “morre”,
aaab – q0 → q1 → q2 → qf isto é, acaba o
processamento. Isso
baa – q0 → q0 → q0 → q0 acontece mesmo que haja
mais símbolos para serem
abaaa – q0 → q1 (indef) lidos.
q0 q1 a q2 a qf
a
a,b
Apsectos Teóricos da Computação 20/25

21. Exemplo
Exemplo: abaixo temos um autômato que aceita todos os strings de 0’s e 1’s que
terminam em 01 e somente eles. O estado q0 é o estado inicial, e podemos pensar que o
autômato está nele até que “adivinhe” que o 01 final começou, É sempre possível que o
próximo símbolo não inicie o 01 final, mesmo que esse símbolo seja 0. Desse modo, o
estado q0 pode fazer uma transição para ele mesmo em 0 e em 1.
Porém, se o próximo símbolo é 0, esse AFND também adivinha que o 01 final começou.
Um arco identificado por 0 leva portanto de q0 a q1. Note que existem dois arcos
rotulados como 0 saindo de q0. O AFND tem a opção de ir para q0 ou q1 e, de fato, ele
segue os dois caminhos. No estado q1 o AFND verifica se o próximo símbolo é 1 e, nesse
caso, vai para o estado q2 e aceita a entrada.
Observe que não existe nenhum arco saindo de q1 rotulado com 0, e não existe nenhum
arco saindo de q2. Nessas situações, o encadeamento no AFND correspondente a esses
a estes estados simplesmente “morre”, embora outros encadeamentos possam continuar
a existir.
0,1
q0 0 q1 1 qf
Apsectos Teóricos da Computação 21/25

22. Função de Transição Estendida
Suponha a string de entrada 00101 para o autômato do
nosso exemplo, teremos a seguinte função de transição
estendida:
δ(q0,00101) = δ(δ(q0,0),0101) =
δ({q0,q1},0101) = δ(δ(q0,0) U δ(q1,0),101) = δ({q0,q1} U Ø,101)
δ({q0,q1},101) = δ(δ(q0,1) U δ(q1,1),01) = δ({q0} U {q2},01)
δ({q0,q2},01) = δ(δ(q0,0) U δ(q2,0),1) = δ({q0,q1} U Ø,1)
δ({q0,q1},1) = δ(q0,1) U δ(q1,1) = {q0} U {q2} = {q0,q2}
0,1
q0 0 q1 1 qf
Apsectos Teóricos da Computação 22/25

23. Não Determinismo e Determinismo
● O não determinismo não aumento o poder
computacional de um autômato.
● Para cada AFN é possível construir um AFD e
vice versa.
Apsectos Teóricos da Computação 23/25

24. Para a Próxima Aula
Ler as seções 3.1, 3.2 e 3.3 do livro texto.
Apsectos Teóricos da Computação 24/25

25. Exercícios
● Lista
Apsectos Teóricos da Computação 25/25