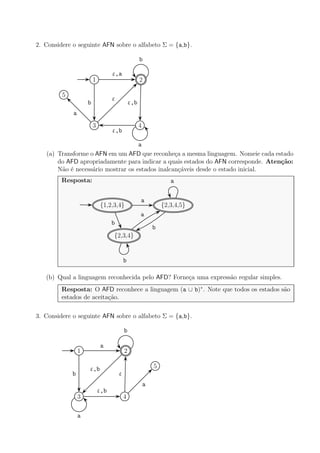
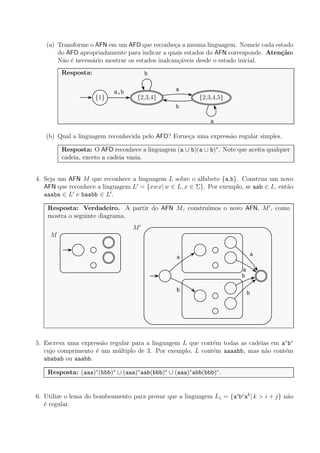
O documento apresenta nove questões sobre autômatos finitos e linguagens regulares. As questões abordam conceitos como: (1) transformação de autômatos finitos não determinísticos em autômatos finitos determinísticos; (2) reconhecimento de linguagens regulares por expressões regulares e autômatos; (3) uso do lema do bombeamento para provar que uma linguagem não é regular.

1. Autˆomatos e Computabilidade: Prova 1
1. Indique se cada uma das seguintes afirma¸c˜oes ´e verdadeira ou falsa, e justifique sua resposta.
Aten¸c˜ao: respostas corretas sem uma justificativa adequada n˜ao receber˜ao pontos. N˜ao ´e
necess´ario fazer provas formais.
(a) Se um AFD M tem k estados, ent˜ao M deve aceitar alguma cadeia de comprimento
pelo menos k − 1.
Resposta: Falso. O conjunto de estados de aceita¸c˜ao de um autˆomato pode ser
vazio, em cujo caso o autˆomato n˜ao aceita nenhuma cadeia.
(b) O conjunto de todas as linguagens regulares sobre o alfabeto Σ = {a} ´e finito.
Resposta: Falso. Os conjuntos {a}, {aa}, {aaa},...s˜ao linguagens regulares, e o
conjunto delas, {{a},{aa},{aaa,. . . } ´e infinito.
(c) A linguagem gerada pela express˜ao regular ∅∗
a∗
´e vazia.
Resposta: Falso. ∅∗
= {ε}; portanto, ∅∗
a∗
=a∗
.
(d) Se L = L1 ∪ L2 e L e L1 s˜ao linguagens regulares, ent˜ao L2 tamb´em ´e regular.
Resposta: Falso. Se L1 ´e a linguagem regular Σ∗
e L2 ´e qualquer linguagem n˜ao
regular sobre Σ, ent˜ao L = L1 ∪ L2 = Σ∗
, que ´e regular.
(e) Se L ´e uma linguagem regular sobre um alfabeto Σ, ent˜ao L′
= {aw| w ∈ L}, onde
a ∈ Σ, tamb´em ´e regular.
Resposta: Verdadeiro. Considere a linguagem regular L′′
= {a}. Ent˜ao,
L′
= L′′
◦ L, que ´e regular, pois a classe das linguagens regulares ´e fechada sobre a
concatena¸c˜ao.
(f) O conjunto de todas as palavras que est˜ao em todos os livros da Biblioteca Central
da UnB, nas quais a quantidade de vogais ´e a mesma que a de consoantes, ´e uma
linguagem regular.
Resposta: Verdadeiro. O conjunto de todas essas palavras ´e finito, e todo con-
junto finito ´e uma linguagem regular. Cada uma das palavras constitui uma lin-
guagem regular com uma ´unica cadeia, pois podemos construir um AFD que aceite
unicamente essa cadeia e rejeite qualquer outra. A uni˜ao de todas essas lingua-
gens tamb´em ´e regular, pois a classe das linguagens regulares ´e fechada sobre essa
opera¸c˜ao.

2. (g) Se um AFN M aceita a cadeia vazia (ε), ent˜ao o estado inicial de M necessariamente
deve ser um estado de aceita¸c˜ao.
Resposta: Falso. O seguinte AFN aceita (ε).
q1 q2
ε
(h) Toda linguagem finita ´e regular.
Resposta: Verdadeiro. Cada uma das cadeias da linguagem constitui uma lin-
guagem regular com uma ´unica cadeia, pois podemos construir um AFD que aceite
unicamente essa cadeia e rejeite qualquer outra. A uni˜ao de todas essas lingua-
gens tamb´em ´e regular, pois a classe das linguagens regulares ´e fechada sobre essa
opera¸c˜ao.
(i) Para cada linguagem regular L, ´e poss´ıvel construir um AFN que reconhe¸ca L e que
tenha um ´unico estado de aceita¸c˜ao.
Resposta: Verdadeiro. Se L ´e regular, ´e reconhecida por algum AFD, que pode
ser transformado em um AFN M1. Para ter um ´unico estado de aceita¸c˜ao, cons-
tru´ımos um novo AFN M, equivalente ao anterior, adicionando setas ε dos estados
de aceita¸c˜ao de M1 a um novo estado de aceita¸c˜ao ´unico, como mostra o seguinte
diagrama.
M1
ε
ε
M
(j) A linguagem gerada pela express˜ao regular ∅a∗
(a ∪ b) ´e vazia.
Resposta: Verdadeiro. Concatenar ∅ a qualquer linguagem produz a linguagem
vazia.
(k) Se L ´e uma linguagem regular e L′
⊆ L, ent˜ao L′
tamb´em ´e regular.
Resposta: Falso. Por exemplo, suponha que L ´e a linguagem regular Σ∗
, e L′
´e
qualquer linguagem n˜ao regular sobre Σ. Ent˜ao, L′
⊆ L.
(l) Para cada AFN com n estados, existe um AFD com um m´aximo de 2n
estados que
reconhece a mesma linguagem que o AFN.
Resposta: Verdadeiro. O m´etodo para transformar um AFN em um AFD equi-
valente, visto em aula, produz um AFD cujos estados s˜ao subconjuntos do AFN. A
quantidade de subconjuntos de estados do AFN ´e 2n
.

3. 2. Considere o seguinte AFN sobre o alfabeto Σ = {a,b}.
1 2
3 4
5
ε,a
b ε,b
b
ε
a
a
ε,b
(a) Transforme o AFN em um AFD que reconhe¸ca a mesma linguagem. Nomeie cada estado
do AFD apropriadamente para indicar a quais estados do AFN corresponde. Aten¸c˜ao:
N˜ao ´e necess´ario mostrar os estados inalcan¸c´aveis desde o estado inicial.
Resposta:
{1,2,3,4} {2,3,4,5}
{2,3,4}
a
b
b
a
a
b
(b) Qual a linguagem reconhecida pelo AFD? Forne¸ca uma express˜ao regular simples.
Resposta: O AFD reconhece a linguagem (a ∪ b)∗
. Note que todos os estados s˜ao
estados de aceita¸c˜ao.
3. Considere o seguinte AFN sobre o alfabeto Σ = {a,b}.
1 2
3 4
5
a
b
ε,b
b
ε,b
a
ε
a

4. (a) Transforme o AFN em um AFD que reconhe¸ca a mesma linguagem. Nomeie cada estado
do AFD apropriadamente para indicar a quais estados do AFN corresponde. Aten¸c˜ao:
N˜ao ´e necess´ario mostrar os estados inalcan¸c´aveis desde o estado inicial.
Resposta:
{1} {2,3,4} {2,3,4,5}
a,b a
b
b
a
(b) Qual a linguagem reconhecida pelo AFD? Forne¸ca uma express˜ao regular simples.
Resposta: O AFD reconhece a linguagem (a ∪ b)(a ∪ b)∗
. Note que aceita qualquer
cadeia, exceto a cadeia vazia.
4. Seja um AFN M que reconhece a linguagem L sobre o alfabeto {a,b}. Construa um novo
AFN que reconhece a linguagem L′
= {xwx| w ∈ L, x ∈ Σ}. Por exemplo, se aab ∈ L, ent˜ao
aaaba ∈ L′
e baabb ∈ L′
.
Resposta: Verdadeiro. A partir do AFN M, constru´ımos o novo AFN, M′
, como
mostra o seguinte diagrama.
M
b
b
a
a
a
b
M′
5. Escreva uma express˜ao regular para a linguagem L que cont´em todas as cadeias em a∗
b∗
cujo comprimento ´e um m´ultiplo de 3. Por exemplo, L cont´em aaaabb, mas n˜ao cont´em
ababab ou aaabb.
Resposta: (aaa)∗
(bbb)∗
∪ (aaa)∗
aab(bbb)∗
∪ (aaa)∗
abb(bbb)∗
.
6. Utilize o lema do bombeamento para provar que a linguagem L1 = {ai
bj
ak
| k > i + j} n˜ao
´e regular.

5. Resposta: Suponha que L1 ´e regular, e que p ´e o comprimento de bombeamento. Con-
sidere a cadeia s =ap
bap+2
∈ L1, cujo comprimento ´e |s| > p. Fazemos s = xyz, onde
|xy| ≤ p e |y| > 0. Ent˜ao, y deve conter somente as; assim, y =an
, onde 0 < n ≤ p0.
Segundo o lema, xyyz ∈ L1. No entanto, xyyz =ap+n
bap+2
. Como p+2 n˜ao ´e maior que
p + n + 1, ent˜ao xyyz /∈ L1. A contradi¸c˜ao indica que L1 n˜ao pode ser regular.
7. Utilize o lema do bombeamento para provar que a linguagem L1 = {ci
bj
ai+j
| i,j > 0} n˜ao
´e regular.
Resposta: Suponha que L1 ´e regular, e que p ´e o comprimento de bombeamento. Con-
sidere a cadeia s =cp
bp
a2p
∈ L1, cujo comprimento ´e |s| > p. Fazemos s = xyz, onde
|xy| ≤ p e |y| > 0. Ent˜ao, y deve conter somente cs; assim, y =cn
, onde 0 < n ≤ p.
Segundo o lema, xyyz ∈ L1. No entanto, xyyz =cn+p
bp
a2p
. Como n + p + p = 2p, ent˜ao
xyyz /∈ L1. A contradi¸c˜ao indica que L1 n˜ao pode ser regular.