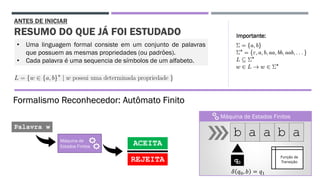
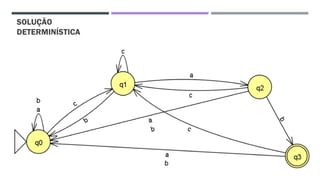
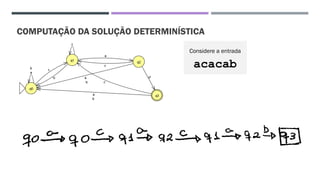
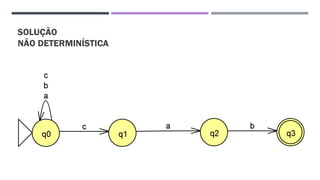
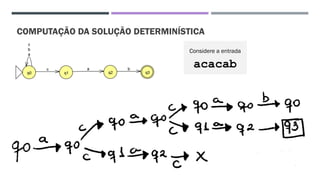
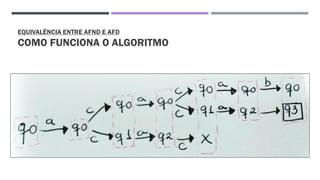
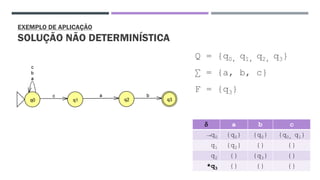
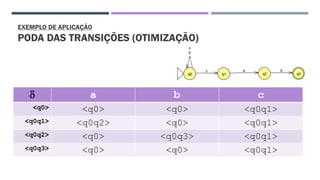
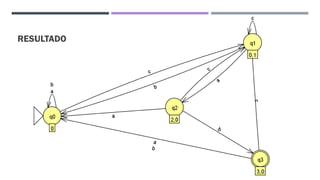
O documento trata da equivalência entre autômatos finitos determinísticos (AFD) e não determinísticos (AFND), abordando suas definições, propriedades e o processo de conversão de um AFND em um AFD. Inclui exemplos de simulações e a construção dos autômatos, além de discutir a computação dos autômatos e as transições dentro deles. A análise culmina na apresentação de um algoritmo que comprova essa equivalência por indução.

1. PROF. WELLINGTON DELLA MURA
CIÊNCIA DA COMPUTAÇÃO (CAMPUS LUIZ MENEGHEL - BANDEIRANTES)
UNIVERSIDADE ESTADUAL DO NORTE DO PARANÁ
Equivalência entre Autômatos Finitos
Determinísticos e Não Determinísticos
Teoria da Computação

2. ROTEIRO
1. Determinismo
2. Não determinismo
3. Computação dos autômatos finitos
4. Equivalência entre AFND e AFD
5. Simulações com JFLAP
6. Resumo da Aula

3. ANTES DE INICIAR
RESUMO DO QUE JÁ FOI ESTUDADO
Máquina de
Estados Finitos
Palavra w
ACEITA
REJEITA
b a a b a
Função de
Transiçãoq0
𝛿 𝑞0, 𝑏 = 𝑞1
• Uma linguagem formal consiste em um conjunto de palavras
que possuem as mesmas propriedades (ou padrões).
• Cada palavra é uma sequencia de símbolos de um alfabeto.
Máquina de Estados Finitos
Formalismo Reconhecedor: Autômato Finito
Importante:

4. AUTÔMATOS
FINITOS
DETERMINÍSTICOS
 Formalismo Reconhecedor
 Recebe uma palavra w e indica se ela é aceita ou rejeitada
 Segue critérios e propriedades da Linguagem Formal L
 Para cada símbolo lido, alterna sua
computação para um novo estado
a b
→q0 q1 q2
Q1 qn -
... ... ...
*qn q1 q2

5. AUTÔMATOS
FINITOS NÃO
DETERMINÍSTICOS
 Da mesma forma que o AFD, recebe uma palavra w e indica se
ela é aceita ou rejeitada
 A principal diferença:
 Para cada símbolo lido, pode alternar sua
computação para
mais de um novo estado
a b
→q0 {q1, ..., qn} {q1, ..., qn}
Q1 {q2, q3} {}
... ... ...
*qn {q2} {q2}

6. EXEMPLO
COMPUTAÇÃO DOS AUTÔMATOS FINITOS
 Considere a linguagem
L = {w ∈ {a, b, c}* | w termina com cab}
 O autômato finito determinístico capaz de reconhecer L pode ter
qualquer prefixo presente em {a, b, c}* mas deve buscar o padrão cab
no final da palavra.
 Por exemplo: ababacab, bbbbcab, cabcab

7. SOLUÇÃO
DETERMINÍSTICA

8. COMPUTAÇÃO DA SOLUÇÃO DETERMINÍSTICA
acacab
Considere a entrada

9. SOLUÇÃO
NÃO DETERMINÍSTICA

10. COMPUTAÇÃO DA SOLUÇÃO DETERMINÍSTICA
acacab
Considere a entrada

11. ALGORITMO
EQUIVALÊNCIA ENTRE AFND E AFD
 Prova: (por indução)
 Mostra que
 a partir de um AFND M qualquer
 É possível construir um AFD MD que realize as mesmas computações
 MD simula M
 Logo, AFND → AFD
 estados de MD simulam combinações de estados alternativos de M

12. EQUIVALÊNCIA ENTRE AFND E AFD
COMO FUNCIONA O ALGORITMO

13. EQUIVALÊNCIA ENTRE AFND E AFD
DEFINIÇÃO FORMAL DO ALGORITMO
M = (, Q, , q0, F) um AFN qualquer.
AFD construído MD = (, QD, D, q0, FD)
• QD – todas as combinações, sem repetições, de estados de Q
• notação q1q2qn
• ordem não distingue combinações: quqv = qvqu
• imagem de todos os estados alternativos de M
• D: QD   → QD
D(q1qn, a) = p1pm sse *({ q1, , qn }, a) = { p1, , pm } em particular:
D(q1qn, a) é indefinida sse *({ q1, , qn }, a) = 
• q0 – estado inicial
• FD - conjunto de estados q1q2qn pertencentes a QD
 alguma componente qi pertence a F, para i em { 1, 2, , n }

14. EXEMPLO DE APLICAÇÃO
SOLUÇÃO NÃO DETERMINÍSTICA
Q = {q0, q1, q2, q3}
∑ = {a, b, c}
F = {q3}
 a b c
→q0 {q0} {q0} {q0, q1}
q1 {q2} {} {}
q2 {} {q3} {}
*q3 {} {} {}

15. EXEMPLO DE APLICAÇÃO
CONSTRUÇÃO DOS ESTADOS
∑ = {a, b, c} se mantém
Q = {q0, q1, q2, q3}
Qd = 2Q
↳ 2Q ={{q0},{q1},{q2},{q2},{q0, q1}... }
q0d = <q0>
F = {q3}
Fd = {<q1q3>, <q0q3>, <q1q2q3>,...}
↳ Todo estado de Fd que contém um elemento de F
q0 q1 q2 q3 estado
0 0 0 1 <q3>
0 0 1 0 <q2>
0 0 1 1 <q2q3>
0 1 0 0 <q1>
0 1 0 1 <q1q3>
0 1 1 0 <q1q2>
0 1 1 1 <q1q2q3>
...
1 1 1 1 <q1q2q3q4>

16. EXEMPLO DE APLICAÇÃO
CONSTRUÇÃO DAS TRANSIÇÕES
Qd = {{q0},{q1},{q2},{q2},{q0, q1}... }
Para d (<q0>, c) => (q0, c)
(q0, c) = {q0, q1}
↳ d(<q0>, c) = <q0q1>
Para d (<q0q1>, a) => (q0, a)  (q1, a)
(q0, a) = {q0}
(q1, a) = {q2}
↳ d(<q0q1>, a) = <q0q2>
 a b c
<q0> <q0> <q0> <q0q1>
<q1> <q2> - -
<q2> - <q3> -
<q3> - - -
<q0q1> <q0q2> <q0> <q0q1>
...
<q0q1q2q3> <q0q2> <q0q3> <q0q1>

17. EXEMPLO DE APLICAÇÃO
CONSTRUÇÃO DAS TRANSIÇÕES
Qd = {{q0},{q1},{q2},{q2},{q0, q1}... }
Para d (<q0>, c) => (q0, c)
(q0, c) = {q0, q1}
↳ d(<q0>, c) = <q0q1>
Para d (<q0q1>, a) => (q0, a)  (q1, a)
(q0, a) = {q0}
(q1, a) = {q2}
↳ d(<q0q1>, a) = <q0q2>
 a b c
<q0> <q0> <q0> <q0q1>
<q1> <q2> - -
<q2> - <q3> -
<q3> - - -
<q0q1> <q0q2> <q0> <q0q1>
...
<q0q1q2q3> <q0q2> <q0q3> <q0q1>

18. EXEMPLO DE APLICAÇÃO
PODA DAS TRANSIÇÕES (OTIMIZAÇÃO)
 a b c
<q0> <q0> <q0> <q0q1>
<q0q1> <q0q2> <q0> <q0q1>
<q0q2> <q0> <q0q3> <q0q1>
<q0q3> <q0> <q0> <q0q1>

19. RESULTADO