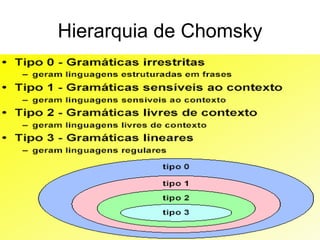
1. O documento descreve gramáticas livres de contexto, que são um tipo de gerador de linguagem formal. 2. Uma gramática livre de contexto é definida como uma quádrupla composta por um alfabeto, conjunto de terminais, conjunto de regras e símbolo inicial. 3. Exemplos de aplicações incluem descrever estruturas de linguagens de programação e elaborar componentes de analisadores sintáticos de compiladores.

1. Gramáticas e Linguagens Formais Cid Soares Eric Silva Lázaro Júnior

2. Gramáticas livres de contexto Reconhecedor de linguagens – Sentido ou não de sentenças(autômatos finitos); Gerador de linguagens – Produzir sentenças, gerar linguagens(conjunto de todas as cadeias produzidas), Ex: expressões regulares; Gramáticas livres de Contexto – Um tipo mais complexo de geradores de linguagem;

3. Definição Uma gramática livre de contexto G é uma quádrupla (V,E,R, S), onde V é um alfabeto, E(o conjunto de terminais ) é um subconjunto de V , R (o conjunto de regras ) é um subconjunto finito de (V -E ) × V* , e S (o símbolo inicial ) é um elemento de V-E

4. Exemplo Uma gramática livre de contexto para os palíndromos: 1. P -> ε 2. P -> 0 3. P -> 1 4. P -> 0P0 5. P -> 1P1

5. Conjunto de Terminais? Existe um conjunto finito de símbolos que formam os strings da linguagem que está sendo definida. Em nosso exemplo, {0,1}. Chamamos esse alfabeto de terminais ou de símbolos terminais.

6. Não Terminais Existe um conjunto finito de variáveis, também chamada às vezes não terminais ou categorias sintáticas. Cada variável representa uma linguagem; isto é, um conjunto de strings. Em nosso exemplo anterior, havia apenas uma variável P.

7. Variáveis Uma das variáveis representa a linguagem que está sendo definida; ela é chamada de símbolo de início. Outras variáveis representam classes auxiliares de strings que são usadas para ajudar a definir a linguagem do símbolo de início. Em nosso exemplo, P (a única variável) é o símbolo de início.

8. Derivações que utilizam uma gramática Tomam-se os strings que sabemos estarem na linguagem de cada uma das variáveis do corpo, concatenamos esses strings na ordem apropriada com quaisquer terminais que apareçam no corpo e 3 inferimos que a string resultante está na linguagem da variável que aparece na cabeça. Esse procedimento é chamado referência recursiva.

9. Derivações que utilizam uma gramática Uma outra abordagem é definir a linguagem para uma gramática, na qual usamos as produções da cabeça para o corpo, expandimos o símbolo da cabeça usando uma de suas produções. Expandimos ainda mais o string resultante substituindo uma de suas variáveis pelo corpo de uma de suas produções e assim sucessivamente, até derivarmos uma string consistindo inteiramente de terminais. A linguagem da gramática é formada por todas as strings de terminais que puderem ser obtidos dessa maneira. Esse procedimento é chamado derivação.

10. Linguagem de uma gramática Se G=(V,T,P,S) é uma GLC, a linguagem de G, detonada por L(G), é o conjunto de strings terminais que têm derivações desde o símbolo de início.

11. Gramáticas Livres de Contexto • Descrever a estrutura de linguagem de programação e os conjuntos de cadeias inter-relacionadas; Elaborar componente analisador sintático de um compilador; Potentes pra descrever a sintaxe das linguagens de programação; Bastante simples pra permitir a criação de analisadores eficientes;

12. Linguagens Formais Estudo de modelos matemáticos que possibilitam a especificação e o reconhecimento de linguagens (no sentido amplo da palavra), suas classificações, estruturas, propriedades, características e inter-relacionamentos.

13. Gramática Formal Conjunto de regras capaz de gerar todas as possibilidades combinatórias desta linguagem. Essa linguagem pode ser uma linguagem formal ou linguagem natural . Gramática livre de contexto é uma notação formal para expressar tais definições recursivas de linguagens.

14. Linguagens livres de Contexto Trata questões: Parênteses balanceados, construções bloco-estruturadas; Típicas de linguagens de programação como Pascal, C e Java; Aplicações: Analisadores sintáticos, tradutores de linguagens e processadores de texto em geral.

15. Chomsky definiu estas classes como (potenciais) modelos para linguagens naturais;

16. Hierarquia de Chomsky

17. Gramática Com Estrutura de Frase Também conhecida como Tipo 0, são aquelas às quais nenhuma limitação é imposta. O universo das linguagens que se podem definir através dos mecanismos gerativos definidos pela gramática corresponde exatamente ao conjunto das linguagens que esta classe de gramática é capaz de gerar.

18. Gramáticas Sensíveis Ao Contexto Também conhecida como Tipo 1. Se as regras de substituição forem sujeitas à restrição de que nenhuma substituição possa reduzir o comprimento da forma sentencial à qual a substituição é aplicada, cria-se uma classe chamada sensíveis ao contexto ou tipo 1.

19. Gramáticas Livres de Contexto Também conhecida como de Tipo 2, são aquelas em que é levantado o condicionamento das substituições impostas pelas regras definidas pelas produções.

20. Gramáticas Regulares Também conhecida como de Tipo 3, é uma restrição sobre a forma das produções, pode-se criar uma nova classe de gramáticas de grande importância no estudo dos compiladores por possuírem propriedades adequadas para a obtenção de reconhecedores simples. Também pode ser denominada de Expressão Regular .

21. FIM! « A ciência é aquilo que compreendemos o suficiente para explicar a um computador. A arte é todo o resto. » Donald Ervin Knuth 1996