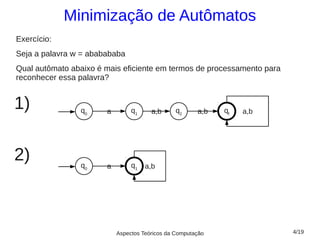
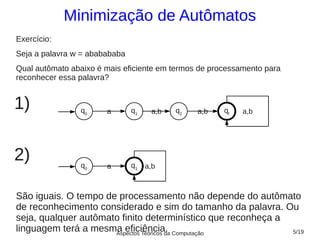
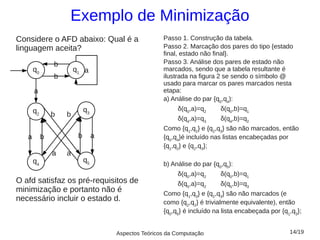
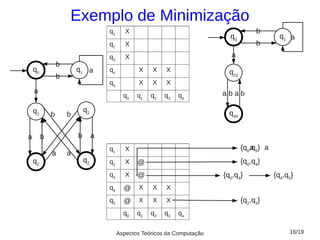
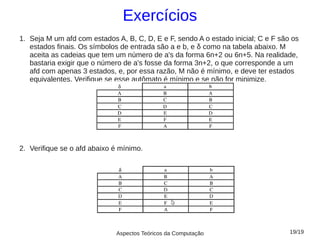
Este documento apresenta os conceitos de minimização de autômatos finitos determinísticos (AFD) em 3 frases: 1) Apresenta os pré-requisitos e o algoritmo de minimização de AFD que identifica estados equivalentes e os unifica para gerar o autômato finito mínimo com o menor número de estados possível; 2) Discutem exemplos para ilustrar a aplicação do algoritmo de minimização, incluindo a construção de uma tabela de estados e marcação dos estados equivalentes; 3) Encerra apresentando

1. Curso: Ciência da Computação
Aspectos Teóricos da Computação
Aula 10
Minimização de um Autômato Finito

2. Notas de Aula
Aspectos Teóricos da Computação 2/19

3. Minimização de um Autômato Finito
● A implementação de um AFD consiste
basicamente em um algoritmo que controla a
mudança de estado do autômato a cada
símbolo lido da entrada.
● O tempo necessário par aceitar ou rejeitar é
diretamente proporcional ao tamanho da
entrada.
● Em termos de complexidade de algoritmos, AF
pertencem à classe de algoritmos mais
eficientes em termos de tempo de
processamento. (Supondo que toda a a fita de
entrada necessita ser lida)
Aspectos Teóricos da Computação 3/19

4. Minimização de Autômatos
Exercício:
Seja a palavra w = ababababa
Qual autômato abaixo é mais eficiente em termos de processamento para
reconhecer essa palavra?
1) q0 a q1 a,b q2 a,b qf a,b
2) q0 a q1 a,b
Aspectos Teóricos da Computação 4/19

5. Minimização de Autômatos
Exercício:
Seja a palavra w = ababababa
Qual autômato abaixo é mais eficiente em termos de processamento para
reconhecer essa palavra?
1) q0 a q1 a,b q2 a,b qf a,b
2) q0 a q1 a,b
São iguais. O tempo de processamento não depende do autômato
de reconhecimento considerado e sim do tamanho da palavra. Ou
seja, qualquer autômato finito determinístico que reconheça a
linguagem terá a mesma eficiência. Computação
Aspectos Teóricos da 5/19

6. Minimização de Autômatos
● O tempo de processamento não depende do autômato de
reconhecimento considerado e sim do tamanho da palavra. Ou
seja, qualquer autômato finito determinístico que reconheça a
linguagem terá a mesma eficiência.
● No entanto podemos trabalhar para minimizar o número de
estados de um autômato se isso for possível.
● Dado um AFD qualquer, o objetivo da minimização é gerar o AF
equivalente com o menor número de estados possíveis
denominado Autômato Finito Determinístico Mínimo ou
simplesmente Autômato Finito Mínimo.
● O AFM é único. Assim dois autômatos distintos que aceitam a
mesma linguagem, ao serem minimizados, geram o mesmo
autômato finito mínimo.
● Basicamente, o algoritmo de minimização unifica os estados
equivalentes.
Aspectos Teóricos da Computação 6/19

7. Estados Equivalentes
Estados equivalentes
Seja M= (∑, Q, δ,q0, F) um AFD qualquer. Dois estados q e p de Q
são ditos equivalentes se, e somente se, para qualquer palavra w
pertencente a ∑*, δ(q,w) e δ(p,w) resultam simultaneamente em
estados finais, ou não finais.
Portanto o processamento de uma entrada qualquer a partir de
estados equivalentes resulta na mesma condição de aceita/rejeita.
Aspectos Teóricos da Computação 7/19

8. Autômato Finito Mínimo
Para uma dada linguagem regular L, o
correspondente AFDM ou simplesmente AFM é
um autômato finito determinístico:
Mm= (∑, Qm, δm,q0m, Fm)
tal que ACEITA(Mm) = L e que, para qualquer
outro autômato finito determinístico M= (∑, Q,
δ,q0, F) tal que ACEITA(M)=L, ocorre:
#Q ≥ #Qm
Aspectos Teóricos da Computação 8/19

9. Pré-Requisitos do Algoritmo de Minimização
(a)Deve ser determinístico
(b)Todos os estados do autômato devem ser
estados alcançáveis a partir do estado inicial,
Ou seja, não pode haver estados inacessíveis;
(c)A função de transição deve ser total (a partir
de qualquer estado, são previstas transições
para todos os símbolos do alfabeto)
Caso o A não satisfaça algum desse pre-reqs,
ele deve ser modificado seguindo as regras do
slide seguinte.
Aspectos Teóricos da Computação 9/19

10. ● Gerar um autômato determinístico equivalente.
● Eliminar os estados inacessíveis e suas
correspondentes transições.
● Para transformar a função de transição em
total, é suficiente introduzir um novo estado
não final d e incluir as transições não previstas,
tendo d como estado destino. Por fim, incluir
um ciclo em d para todos os símbolos do
alfabeto.
Aspectos Teóricos da Computação 10/19

11. Algoritmo de Minimização
O algoritmo abaixo identifica os estados equivalentes por exclusão. A partir de uma
tabela são marcados os estados não equivalentes. Ao final do algoritmo, as referências
não marcadas representam os estados equivalentes.
Suponha um AFD M= (∑, Q, δ,q0, F) que satisfaz à observação anterior – Pré Requisitos
do Algoritmo de Minimização. - Os passos dos algoritmo são os seguintes:
1. Construção da tabela. Construir uma tabela, relacionando os estados distintos,
sendo que cada par (não ordenado) de estados ocorre somente uma vez, como
ilustrado a seguir.
2. Marcação dos Estados Trivialmente Não-Equivalentes. Marcar todos os pares do tipo
{estado final, estado não final}, pois obviamente, estados finais não são equivalentes
a não-finais;
3. Marcação dos Estados Não-Equivalentes. Para cada par (qu,qv} não marcado e para
cada símbolo a Є ∑, suponha que: δ(qu,a)=pu e δ(qv,a)=pv
Assim:
(a) Se pu=pv, então qu é equivalente a qv para o símbolo a e não deve ser marcado;
(b) Se pu≠pv e o par {pu,pv} não está marcado, então {qu,qv} é incluído em uma lista a
partir de {pu,pv} para posterior análise;
(c) Se pu≠pv e o par {pu,pv} está marcado, então:
● {qu,qv} não é equivalente e deve ser marcado;
● Se {qu,qv} encabeça uma lista de pares, então marcar todos os pares da lista
(e, recursivamente, se algum par da lista encabeça outra lista);
Aspectos Teóricos da Computação 11/19

12. Algoritmo de Minimização
4. Unificação dos Estados Equivalentes. Os estados dos pares não marcados são
equivalentes e podem ser unificados como segue:
● a equivalência dos estados é transitiva;
● pares de estados não-finais equivalentes podem ser unificados como um único
estado não-final;
● pares de estados finais equivalentes podem ser unificados como um único
estado final;
● se algum dos estados equivalentes é inicial, então o correspondente estado
unificado é inicial;
● todas as transações como origem (respectivamente destino) em um estado
equivalente, são preservadas, mas passam a ter origem (respectivamente,
destino) no correspondente estado unificado;
5. Exclusão dos Estados Inúteis. Por fim, os estados chamados inúteis devem ser
excluídos. Um estado q é dito um estado inútil se é não-final e a partir de q não é
possível atingir um estado final. Deve-se observar que o estado d (se incluído)
sempre é inútil (o algoritmo para excluir os estados inúteis é simples). Todas as
transições com origem ou destino em um estado inútil são excluídas.
Aspectos Teóricos da Computação 12/19

13. Algoritmo de Minimização
q1
q2
...
qn
d
q0 q1 ... qn-1 qn
Aspectos Teóricos da Computação 13/19

14. Exemplo de Minimização
Considere o AFD abaixo: Qual é a Passo 1. Construção da tabela.
linguagem aceita? Passo 2. Marcação dos pares do tipo {estado
final, estado não final}.
b Passo 3. Análise dos pares de estado não
q0 q1 a marcados, sendo que a tabela resultante é
b ilustrada na figura 2 se sendo o símbolo @
usado para marcar os pares marcados nesta
a etapa:
a) Análise do par {q0,q4):
q2 q3 δ(q0,a)=q2 δ(q0,b)=q1
b b
δ(q4,a)=q3 δ(q4,b)=q2
Como {q1,q2} e {q2,q3} são não marcados, então
a b b a {q0,q4}é incluído nas listas encabeçadas por
{q1,q2} e {q2,q3};
a a
q4 q5
b) Análise do par {q0,q5):
δ(q0,a)=q2 δ(q0,b)=q1
O afd satisfaz os pré-requisitos de δ(q5,a)=q2 δ(q5,b)=q3
minimização e portanto não é Como {q1,q3} e {q2,q3} são não marcados (e
necessário incluir o estado d. como {q2,q2} é trivialmente equivalente), então
{q0,q5} é incluído na lista encabeçada por {q1,q3};
Aspectos Teóricos da Computação 14/19

15. Exemplo de Minimização
c) Análise do par {q1,q2): f) Análise do par {q4,q5):
δ(q1,a)=q1 δ(q1,b)=q0 δ(q4,a)=q3 δ(q4,b)=q2
δ(q2,a)=q4 δ(q2,b)=q5 δ(q5,a)=q2 δ(q5,b)=q3
Como {q1,q4} é marcado, então {q1,q2} também é Como {q2,q3} é não marcado, então {q4,q5} é
marcado. Como {q1,q2} encabeça uma lista, o incluído na lista encabeçada por {q2,q3};
par {q0,q4} também é marcado ;
Passo 4. Como os pares {q2,q3} e {q4,q5} são não
d) Análise do par {q1,q3): marcados, as seguintes unificações podem ser
δ(q1,a)=q1 δ(q1,b)=q0 feitas:
● q23 representa a unificação dos estados não
δ(q3,a)=q5 δ(q3,b)=q4
finais q2 e q3.
Como {q1,q5} bem como {q0,q4} são marcados,
● q45 representa a unificação dos estados
então {q1,q3} também é marcado. Como {q1,q3}
finais q4 e q5.
encabeça uma lista, o par {q0,q5} também é
marcado ;
O autômato mínimo resultante possui quatro
estados e é ilustrado na figura a seguir. Observe
e) Análise do par {q2,q3): a preservação das transições cujos estados
δ(q2,a)=q4 δ(q2,b)=q5 origem ou destino foram unificados.
δ(q3,a)=q5 δ(q3,b)=q4
Como {q4,q5} é não marcado, então {q2,q3} é
incluído na lista encabeçada por {q4,q5}
Aspectos Teóricos da Computação 15/19

16. Exemplo de Minimização
q1 X b
q0 q1 a
q2 X b
q3 X a
b
q0 q1 a q4 X X X q23
b
q5 X X X
a a,b a,b
q0 q1 q2 q3 q4
q2 q2 q45
b b
a b b a
q1 X {q0,q5} a
a
a a
q2 q2 q2 X @ {q0,q4}
q3 X @ {q0,q4} {q4,q5}
q4 @ X X X
q5 @ X X X {q2,q3}
q0 q1 q2 q3 q4
Aspectos Teóricos da Computação 16/19

17. Teoremas
Teorema Autômato Finito Mínimo
O autômato construído usando o algoritmo de
minimização apresentado é um autômato finito
determinístico com menor número de estados
que aceita a linguagem.
Teorema Unicidade do Autômato Finito Mínimo
O autômato finito determinístico mínimo de uma
linguagem é único.
Aspectos Teóricos da Computação 17/19

18. Ler
● Seçao 4.6 do livro.
Aspectos Teóricos da Computação 18/19

19. Exercícios
1. Seja M um afd com estados A, B, C, D, E e F, sendo A o estado inicial; C e F são os
estados finais. Os símbolos de entrada são a e b, e δ como na tabela abaixo. M
aceita as cadeias que tem um número de a's da forma 6n+2 ou 6n+5. Na realidade,
bastaria exigir que o número de a's fosse da forma 3n+2, o que corresponde a um
afd com apenas 3 estados, e, por essa razão, M não é mínimo, e deve ter estados
equivalentes. Verifique se esse autômato é mínimo e se não for minimize.
2. Verifique se o afd abaixo é mínimo.
Aspectos Teóricos da Computação 19/19