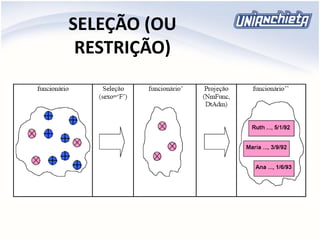
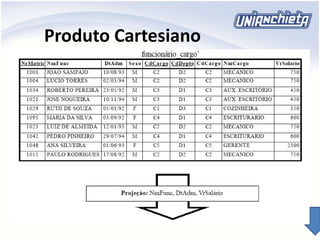
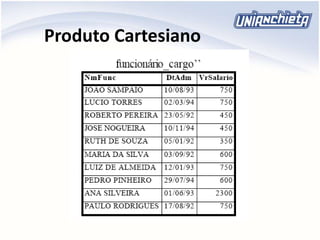
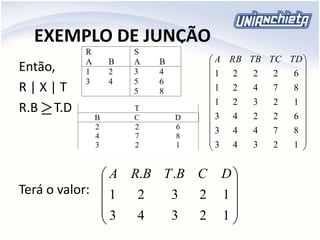
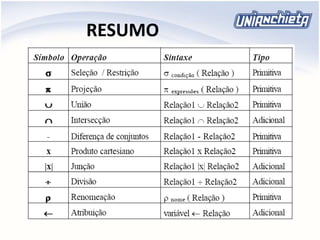
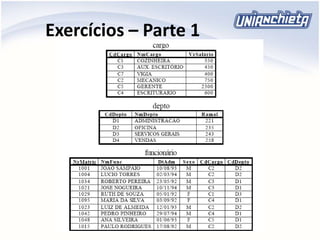
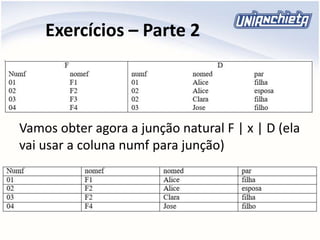
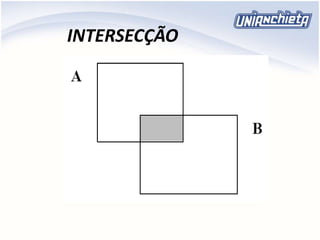
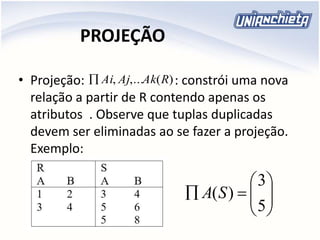
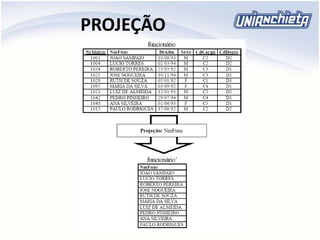
O documento apresenta os principais conceitos da álgebra relacional, incluindo operadores como união, intersecção, diferença, projeção, seleção e produto cartesiano. Estes operadores permitem manipular e combinar dados armazenados em tabelas relacionais de um banco de dados. Exemplos ilustram como aplicar cada operador para extrair informações específicas de uma ou mais tabelas.


















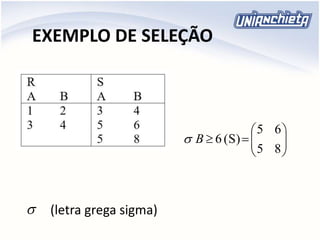




![EXEMPLO DE SELEÇÃO
(OU RESTRIÇÃO)
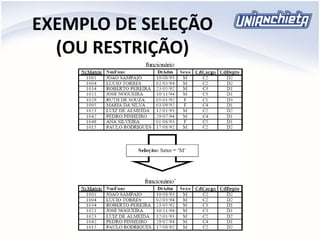
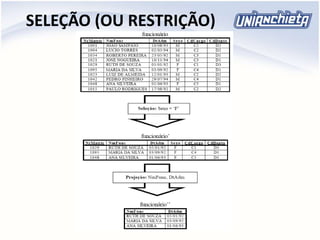
Ex.: Sexo = ‘M’ (funcionário)
Produz o conjunto dos elementos de funcionário
que atendem ao predicado [Sexo = ‘M’], ou seja,
representa um subconjunto dos funcionários
para o qual essa condição é avaliada como
verdadeira.
](https://image.slidesharecdn.com/bdi-aula08a-algebrarelacional-190925030635/85/BD-I-Aula-08-A-Algebra-Relacional-27-320.jpg)