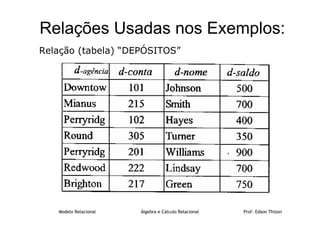
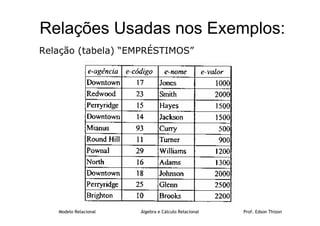
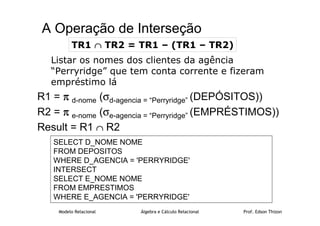
O documento discute as linguagens de consulta formal Álgebra Relacional e Cálculo Relacional. A Álgebra Relacional fornece operadores como seleção, projeção e produto cartesiano que podem ser combinados para extrair informações de uma base de dados. O Cálculo Relacional estende a Álgebra Relacional com quantificadores universal e existencial. Exemplos ilustram como essas operações podem ser usadas para consultas em tabelas de um banco de dados relacional.

1. Álgebra Relacional
e
Cálculo Relacional
Prof. Edson Thizon
SISTEMAS DE INFORMAÇÃO

2. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
Linguagens de consultas formais (1)
Uma linguagem de consulta (Query Language) é uma
linguagem com a qual o usuário pode requisitar ao
Sistema de Gerência de Banco de Dados (SGBD)
informações armazenadas no Banco de Dados (BD).
Linguagens de consulta podem ser:
– Procedurais
• O usuário descreve o algoritmo de acesso aos
dados através de uma seqüência de instruções
(COMO)
– Não procedurais
• O usuário descreve a informação que deseja obter
sem descrever como obtê-la (O QUÊ)

3. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
Linguagens de consultas formais (2)
As linguagens de consulta e atualização comerciais
para sistemas relacionais baseiam-se na ÁLGEBRA
RELACIONAL (procedural) e no CÁLCULO
RELACIONAL (não procedural)
As operações da álgebra e do cálculo exprimem o
conjunto de consultas e manipulações possíveis
sobre uma base de dados relacional qualquer

4. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
A álgebra apresenta o conjunto mínimo de
OPERADORES RELACIONAIS que podem ser
combinados para extrair da base de dados,
praticamente, todas as informações ali
armazenadas (dados e seus relacionamentos)
O cálculo estende (e completa) a potencialidade
da álgebra relacional com a introdução dos
quantificadores universal (∀) e existencial (∃)
Linguagens de consultas formais (3)

5. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
Álgebra Relacional (AR)
Operações fundamentais da Álgebra Relacional:
– Restrição/Seleção (select): σ
– Projeção (project): π
– Produto Cartesiano (cartesian product): x
– União (union): ∪
– Diferença (set-difference): -

6. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
Álgebra Relacional (AR)
Além das 5 operações fundamentais, a Álgebra
Relacional oferece as operações:
– INTERSEÇÃO: ∩
– JUNÇÃO THETA: Ξθ
– JUNÇÃO NATURAL: Ξ
– DIVISÃO: ÷

7. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
Operações Fundamentais da
Álgebra Relacional
SELEÇÃO e PROJEÇÃO são operações
UNÁRIAS.
As outras três operações (PRODUTO
CARTESIANO, UNIÃO e DIFERENÇA) operam,
cada uma, sobre um par de relações.
As operações da AR sempre operam sobre
relações e devolvem como resultado uma
relação.

8. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
Relações Usadas nos Exemplos:
Relação (tabela) “CLIENTES”

9. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
Script Tabela Clientes
CREATE TABLE CLIENTES
(C_NOME VARCHAR2(20) NOT NULL PRIMARY KEY,
C_ENDERECO VARCHAR2(20) NOT NULL,
C_CIDADE VARCHAR2(20) NOT NULL);
INSERT INTO CLIENTES(C_NOME, C_ENDERECO, C_CIDADE) VALUES ('JONES','MAIN','HARRISON');
INSERT INTO CLIENTES(C_NOME, C_ENDERECO, C_CIDADE) VALUES ('SMITH','NORTH','RYE');
INSERT INTO CLIENTES(C_NOME, C_ENDERECO, C_CIDADE) VALUES ('HAYES','MAIN','HARRISON');
INSERT INTO CLIENTES(C_NOME, C_ENDERECO, C_CIDADE) VALUES ('CURRY','NORTH','RYE');
INSERT INTO CLIENTES(C_NOME, C_ENDERECO, C_CIDADE) VALUES ('LINDSAY','PARK','PITTSFIELD');
INSERT INTO CLIENTES(C_NOME, C_ENDERECO, C_CIDADE) VALUES ('TURNER','PUTNAM','STAMFORD');
INSERT INTO CLIENTES(C_NOME, C_ENDERECO, C_CIDADE) VALUES ('WILLIAMS','NASSAU','PRINCETON');
INSERT INTO CLIENTES(C_NOME, C_ENDERECO, C_CIDADE) VALUES ('ADAMS','SPRING','PITTSFIELD');
INSERT INTO CLIENTES(C_NOME, C_ENDERECO, C_CIDADE) VALUES ('JOHNSON','ALMA','PALO ALTO');
INSERT INTO CLIENTES(C_NOME, C_ENDERECO, C_CIDADE) VALUES ('GLENN','SAND HILL','WOODSIDE');
INSERT INTO CLIENTES(C_NOME, C_ENDERECO, C_CIDADE) VALUES ('BROOKS','SENATOR','BROOKLYN');
INSERT INTO CLIENTES(C_NOME, C_ENDERECO, C_CIDADE) VALUES ('GREEN','WALNUT','STAMFORD');
INSERT INTO CLIENTES(C_NOME, C_ENDERECO, C_CIDADE) VALUES ('JACKSON','WAL','FORD');
COMMIT;

10. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
Relações Usadas nos Exemplos:
Relação (tabela) “DEPÓSITOS”

11. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
Script Tabela Depósitos
CREATE TABLE DEPOSITOS
(D_AGENCIA VARCHAR2(20) NOT NULL,
D_CONTA NUMBER(10) NOT NULL,
D_NOME VARCHAR2(20) NOT NULL,
D_SALDO NUMBER(10,2) NOT NULL,
CONSTRAINT DEPOSITOS_CLIENTES_FK FOREIGN KEY (D_NOME)
REFERENCES CLIENTES (C_NOME));
INSERT INTO DEPOSITOS(D_AGENCIA,D_CONTA, D_NOME, D_SALDO) VALUES('DOWNTOW',101, 'JOHNSON',500);
INSERT INTO DEPOSITOS(D_AGENCIA,D_CONTA, D_NOME, D_SALDO) VALUES('MIANUS',215, 'SMITH',700);
INSERT INTO DEPOSITOS(D_AGENCIA,D_CONTA, D_NOME, D_SALDO) VALUES('PERRYRIDGE',102, 'HAYES',400);
INSERT INTO DEPOSITOS(D_AGENCIA,D_CONTA, D_NOME, D_SALDO) VALUES('ROUND',305, 'TURNER',350);
INSERT INTO DEPOSITOS(D_AGENCIA,D_CONTA, D_NOME, D_SALDO) VALUES('PERRYRIDGE',201, 'WILLIAMS',900);
INSERT INTO DEPOSITOS(D_AGENCIA,D_CONTA, D_NOME, D_SALDO) VALUES('REDWOOD',222, 'LINDSAY',700);
INSERT INTO DEPOSITOS(D_AGENCIA,D_CONTA, D_NOME, D_SALDO) VALUES('BRIGHTON',217, 'GREEN',750);
COMMIT;

12. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
Relações Usadas nos Exemplos:
Relação (tabela) “EMPRÉSTIMOS”

13. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
Script Tabela Empréstimos
CREATE TABLE EMPRESTIMOS
(E_AGENCIA VARCHAR2(20) NOT NULL,
E_CODIGO NUMBER(10) NOT NULL,
E_NOME VARCHAR2(20) NOT NULL,
E_VALOR NUMBER(10,2) NOT NULL,
CONSTRAINT EMPRESTIMOS_CLIENTES_FK FOREIGN KEY (E_NOME)
REFERENCES CLIENTES (C_NOME));
INSERT INTO EMPRESTIMOS(E_AGENCIA,E_CODIGO, E_NOME, E_VALOR) VALUES('DOWNTOW',17, 'JONES',1000);
INSERT INTO EMPRESTIMOS(E_AGENCIA,E_CODIGO, E_NOME, E_VALOR) VALUES('REDWOOD',23, 'SMITH',2000);
INSERT INTO EMPRESTIMOS(E_AGENCIA,E_CODIGO, E_NOME, E_VALOR) VALUES('PERRYRIDGE',15, 'HAYES',1500
INSERT INTO EMPRESTIMOS(E_AGENCIA,E_CODIGO, E_NOME, E_VALOR) VALUES('DOWNTOW',14, 'JACKSON',1500
INSERT INTO EMPRESTIMOS(E_AGENCIA,E_CODIGO, E_NOME, E_VALOR) VALUES('MIANUS',93, 'CURRY',500);
INSERT INTO EMPRESTIMOS(E_AGENCIA,E_CODIGO, E_NOME, E_VALOR) VALUES('ROUND HILL',11, 'TURNER',900);
INSERT INTO EMPRESTIMOS(E_AGENCIA,E_CODIGO, E_NOME, E_VALOR) VALUES('PWNAL',29, 'WILLIAMS',1200);
INSERT INTO EMPRESTIMOS(E_AGENCIA,E_CODIGO, E_NOME, E_VALOR) VALUES('NORTH',16, 'ADAMS',1300);
INSERT INTO EMPRESTIMOS(E_AGENCIA,E_CODIGO, E_NOME, E_VALOR) VALUES('DOWNTOW',18, 'JOHNSON',2000
INSERT INTO EMPRESTIMOS(E_AGENCIA,E_CODIGO, E_NOME, E_VALOR) VALUES('PERRYRIDGE',25, 'GLENN',2500
INSERT INTO EMPRESTIMOS(E_AGENCIA,E_CODIGO, E_NOME, E_VALOR) VALUES('BRIGHTON',10, 'BROOKS',2200);
COMMIT;

14. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
Seleciona tuplas (linhas) de uma relação
(tabela) que satisfazem um determinado
predicado (condição)
– Formato:
– Ex.:Selecione as tuplas da relação
EMPRÉSTIMOS para quais o nome da agência é
“Perryridge”
A operação de Seleção
R = σe-agência=‘Perryridge’ (EMPRÉSTIMOS)
RelResultado = σpredicado (RelEntrada)
SELECT *
FROM EMPRESTIMOS
WHERE E_AGENCIA = 'PERRYRIDGE'

15. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
Em geral, os predicados permitem expressar
comparações do tipo (, ≤, , ≥, = e ≠). Além disso,
pode-se relacional com operadores lógicos (and,
or, not)
Exemplos:
– Selecione tuplas da relação EMPRÉSTIMOS para as
quais o valor do empréstimo é maior que 1200:
RelResult = σe-valor1200 (EMPRÉSTIMOS)
– Selecione as tuplas da relação EMPRÉSTIMOS para as
quais o nome da agência é “Perryridge e o valor do
empréstimo excede 1200:
RelResult = σe-valor1200 and e-agencia = ‘Perryridge’(EMPRÉSTIMOS)
A operação de Seleção

16. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
Copia uma relação de entrada, deixando de
fora uma ou mais colunas
– Formato:
– Ex.: Obter uma tabela que relacione os
clientes do banco com as agências onde
fizeram empréstimos:
A Operação de Projeção
Res=πe-agencia, e-nome(EMPRÉSTIMOS)
RelResult=πcolunas a copiar(RelEntrada)
SELECT E_AGENCIA, E_NOME
FROM EMPRESTIMOS

17. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
É possível compor operações mais complexas da
álgebra relacional através do aninhamento de
operações mais simples
Exemplo: listar os nomes dos clientes que fizeram
empréstimos superiores a 1200:
RelResult = π
π
π
πe-nome(σ
σ
σ
σe-valor1200 (EMPRÉSTIMOS))
A operação de seleção que gera uma relação como
resultado pode ser usada como relação de entrada
para a operação de projeção
A Operação de Projeção
SELECT DISTINCT E_NOME
FROM (SELECT E_NOME
FROM EMPRESTIMOS
WHERE E_VALOR 1200)

18. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
O Produto Cartesiano
As operações de seleção e projeção permitem
extrair informações de somente uma relação de
cada vez.
A operação de PRODUTO CARTESIANO permite
relacionar informações de duas relações.
Dadas duas relações de entrada, R1 com N tuplas
e R2 com M tuplas, o produto cartesiano delas é
uma relação, contendo (MxN) tuplas. A operação
CONCATENA cada tupla de R1 com todas as
tuplas de R2.

19. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
O Produto Cartesiano
Quando, devido a concatenação de tuplas de duas relações
diferentes, RelResult apresenta duas colunas de mesmo
nome, cada uma delas recebe, como prefixo, o nome de sua
relação de origem
Exemplo: listar o nome dos clientes que moram em Rye e
fizeram empréstimo de menos de 1000.
a)RelResult1= CLIENTES x EMPRÉSTIMOS
b)RelResult2= σc-name = e-name (RelResult1)
c)RelResult3= σe-valor1000 and c-cidade = Rye (RelResult2)
SELECT C_NOME
FROM CLIENTES, EMPRESTIMOS
WHERE C_NOME = E_NOME AND
E_VALOR 1000 AND C_CIDADE = 'RYE'

20. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
A Operação de União
Considere agora que se deseje listar os clientes associados
à agência de “Perryridge”, independente do seu
relacionamento com aquela agência (depósito ou
empréstimo)
R1 = π
π
π
π d-nome (σd-agencia = “Perryridge” (DEPÓSITOS))
R2 = π
π
π
π e-nome (σe-agencia = “Perryridge” (EMPRÉSTIMOS))
Result = R1 U R2
SELECT D_NOME NOME
FROM DEPOSITOS
WHERE D_AGENCIA = 'PERRYRIDGE'
UNION
SELECT E_NOME NOME
FROM EMPRESTIMOS
WHERE E_AGENCIA = 'PERRYRIDGE'

21. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
A Operação de Diferença
Listar aqueles clientes da agência “Perryridge” que não
fizeram empréstimos naquela agência (têm só conta
corrente lá). O que se pede nesta consulta é o conjunto de
clientes que têm conta na agência menos o conjunto de
nomes de clientes que fizeram empréstimo nesta agência.
R1 = π
π
π
π d-nome (σd-agencia = “Perryridge” (DEPÓSITOS))
R2 = π
π
π
π e-nome (σe-agencia = “Perryridge” (EMPRÉSTIMOS))
Result = R1 - R2
SELECT D_NOME NOME
FROM DEPOSITOS
WHERE D_AGENCIA = 'PERRYRIDGE'
MINUS
SELECT E_NOME NOME
FROM EMPRESTIMOS
WHERE E_AGENCIA = 'PERRYRIDGE'

22. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
Operações de União e Diferença
Para as operações UNIÃO e DIFERENÇA
serem consideradas corretas, duas
condições devem ser satisfeitas:
– As relações R1 e R2 têm que apresentar o
mesmo número de atributos.
– Os domínios (tipo de dado) do i-ésimo atributo
de R1 e do i-ésimo atributo de R2 devem ser
iguais.

23. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
Operadores Adicionais
Os operadores a seguir não acrescentam
qualquer poder à Álgebra Relacional,
somente simplificam a construção de
consultas.

24. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
A Operação de Interseção
A INTERSEÇÃO entre duas relações é uma
relação que contém somente as tuplas
comuns das duas relações argumentos
Os requisitos válidos para a UNIÃO e
DIFERENÇA valem também para a
INTERSEÇÃO

25. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
A Operação de Interseção
Listar os nomes dos clientes da agência
“Perryridge” que tem conta corrente e fizeram
empréstimo lá
R1 = π
π
π
π d-nome (σd-agencia = “Perryridge” (DEPÓSITOS))
R2 = π
π
π
π e-nome (σe-agencia = “Perryridge” (EMPRÉSTIMOS))
Result = R1 ∩
∩
∩
∩ R2
TR1 ∩
∩
∩
∩ TR2 = TR1 – (TR1 – TR2)
SELECT D_NOME NOME
FROM DEPOSITOS
WHERE D_AGENCIA = 'PERRYRIDGE'
INTERSECT
SELECT E_NOME NOME
FROM EMPRESTIMOS
WHERE E_AGENCIA = 'PERRYRIDGE'

26. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
A Operação de Junção Theta
Usualmente, consultas que envolvem o
produto cartesiano de duas relações
incluem também uma operação de seleção
sobre as tuplas do produto.

27. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
A Operação de Junção Theta
A JUNÇÃO THETA é uma operação binária que
combina o produto cartesiano e a seleção em
uma única operação. Por exemplo: listar o nome e
a cidade vive de cada uma dos clientes devedores
da agência “Perryridge”.
π
π
π
π e-nome,c-cidade (σc-nome = e-nome and e-agencia = ‘Perryridge’
(CLIENTES x EMPRÉSTIMOS))
SELECT E_NOME, C_CIDADE
FROM CLIENTES, EMPRESTIMOS
WHERE C_NOME = E_NOME AND
E_AGENCIA = 'PERRYRIDGE'

28. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
Cálculo Relacional de Tuplas
Linguagem NÃO PROCEDURAL (declarativa):
O usuário descreve a INFORMAÇÃO que deseja
obter sem descrever como obtê-la ( O QUÊ)
O Cálculo Relacional de Tuplas (CRT) permite
que se defina conjuntos de tuplas a partir de
expressões do tipo: {t | P(t)}
Uma expressão do cálculo relacional representa
um conjunto de tuplas onde, para cada tupla t, o
predicado P(t) é verdadeiro:
T ∈ Result ⇒ P(t)

29. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
Cálculo Relacional de Tuplas
Uma Variável Tupla (VT) representa, a cada
instante, uma tupla T de uma determinada relação
R. Uma fórmula P(t) pode apresentar mais de uma
variável tupla. Em uma determinada fórmula, uma
VT pode aparecer como:
– Variável Destino: quando estiver associada a um
quantificador existencial ∋ (existe) ou universal ∀ (para
todo)
– Variável Livre: em caso contrário ao anterior
Exemplo:
AR = σe-agencia = ‘Perryridge’ (EMPRÉSTIMOS)
CRT = {t | t ∈ EMPRÉSTIMOS ^ t[e-agencia]=‘Perryridge’}

30. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
Expressando Operação da Álgebra
Relacional em Cálculo Relacional
Selecione as tuplas da relação
EMPRÉSTIMOS para as quais o valor do
empréstimo é maior que 1200.
AR = σe-valor 1200 (EMPRÉSTIMOS)
CRT = {t | t ∈ EMPRÉSTIMOS ^ t[e-valor]1200}

31. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
Expressando Operação da Álgebra
Relacional em Cálculo Relacional
Listar os nomes dos clientes que moram em
Rye e fizeram empréstimo de menos de
1000.
AR = π
π
π
π e-nome (σe-valor1000 and c-cidade = ‘Rye’
(σc-name = e-name (CLIENTES x EMPRÉSTIMOS)))
CRT = {t | ∋ s ∈ CLIENTES (s[c-cidade] = ‘Rye’ ^
∋ u ∈ EMPRÉSTIMOS (s [c-nome] = u[e-nome] ^
u[e-valor]1000 ^ t[e-nome] = u[e-nome]))}

32. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
Com AR (relacionamento)
Com CRT (exists)
SELECT C_NOME
FROM CLIENTES, EMPRESTIMOS
WHERE C_NOME = E_NOME AND
E_VALOR 1000 AND C_CIDADE = 'RYE'
SELECT C_NOME
FROM CLIENTES
WHERE EXISTS (SELECT E_NOME
FROM EMPRESTIMOS
WHERE C_NOME = E_NOME AND
E_VALOR 1000 AND C_CIDADE = 'RYE')

33. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
n Em SQL (Subconsulta)
SQL
SELECT C_NOME
FROM CLIENTES
WHERE C_NOME IN (SELECT E_NOME
FROM EMPRESTIMOS
WHERE E_VALOR 1000 AND C_CIDADE = 'RYE')

34. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
Outer Join
Retorna linhas ausentes na outra tabela. O sinal
de adição (+) é colocado ao lado do join que não
possui as informações. Esse tipo de
relacionamento não pode usar operadores In ou
OR.
O que mudou no resultado? Porque?
SELECT C_NOME
FROM CLIENTES, EMPRESTIMOS
WHERE C_NOME = E_NOME (+) AND
E_VALOR (+) 1000 AND C_CIDADE = 'RYE'

35. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
Uso do Case
create table test_case_when ( a varchar2(5), b varchar2(5) );
insert into test_case_when values ('*','*');
insert into test_case_when values ('+','+');
insert into test_case_when values ('-','-');
insert into test_case_when values ('.','.');
select a,
case
when b = '*' then 'star'
when b = '+' then 'plus'
when b = '-' then 'minus'
else '????'
end
from test_case_when;

36. Modelo Relacional Álgebra e Cálculo Relacional Prof. Edson Thizon
Referências Bibliográficas
KORTH, Henry F. SILBERSCHATZ,
Abraham. Sistemas de Bancos de
Dados, São Paulo. Ed. Makron Books,
1999.
IOCHPE, Cirano. Institudo de
Informática - UFRGS.