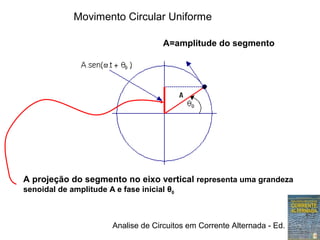
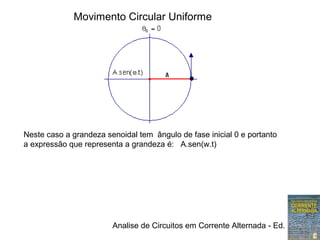
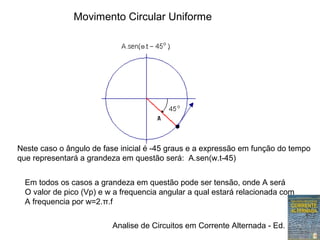
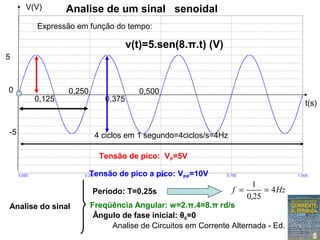
O documento discute representações de tensões alternadas, incluindo:
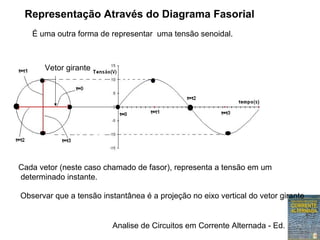
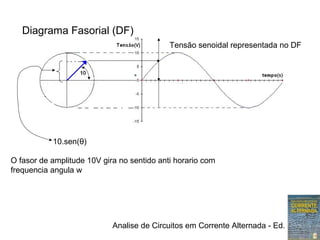
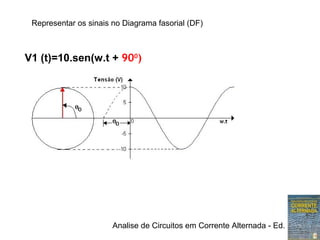
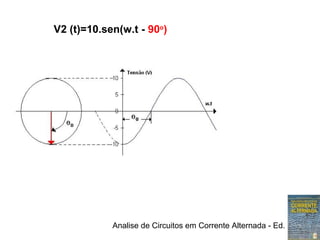
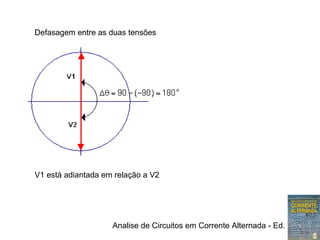
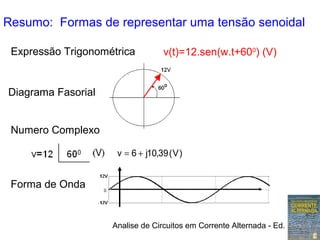
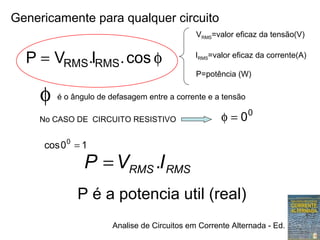
1) Expressões trigonométricas, diagramas fasoriais e números complexos podem representar tensões senoidais
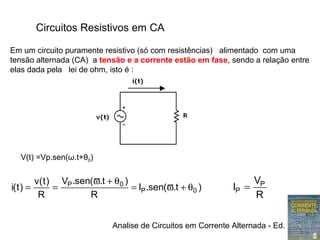
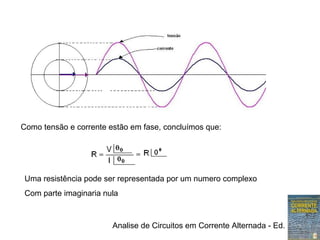
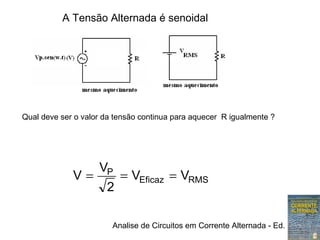
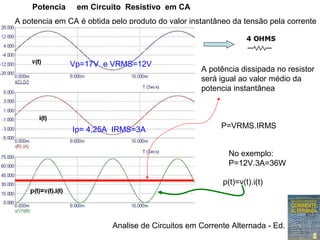
2) Em circuitos resistivos, a tensão e corrente estão em fase e seguem a lei de Ohm
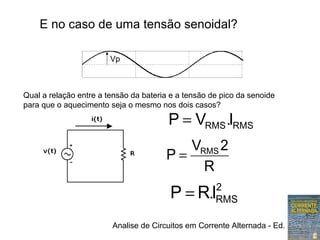
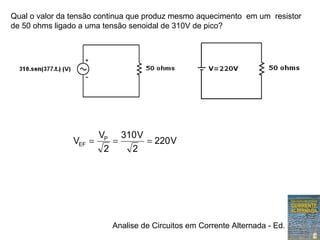
3) O valor eficaz de uma tensão senoidal é igual à tensão contínua que produz o mesmo aquecimento em um resistor
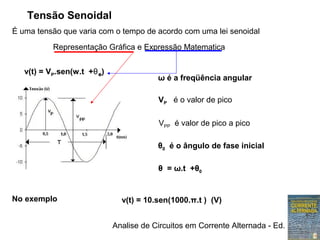

![Analise de Circuitos em Corrente Alternada - Ed. Erica
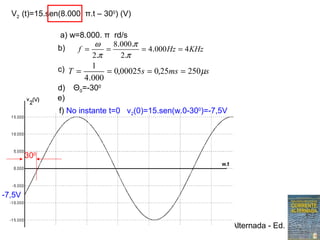
Período (T) e Freqüência (f)
Período (T) é o tempo necessário para o fenômeno voltar a se repetir
(completar um ciclo)
Freqüência (f) é o numero de ciclos completados por segundo
[ ] )(ssegundoT =
[ ] segundocicloouHzf /=
T
f
1
=
f
T
1
=](https://image.slidesharecdn.com/acca02-150405120724-conversion-gate01/85/Acca-02-5-320.jpg)
![Analise de Circuitos em Corrente Alternada - Ed. Erica
Freqüência Angular (ω)
Representa a variação angular em função do tempo
[ ] sgrausousrd //=ω
θ = ω.t
Se θ=2.π, o tempo será t= T
2.π = ω.T fou
T
..
.
πω
π
ω 2
2
==](https://image.slidesharecdn.com/acca02-150405120724-conversion-gate01/85/Acca-02-6-320.jpg)