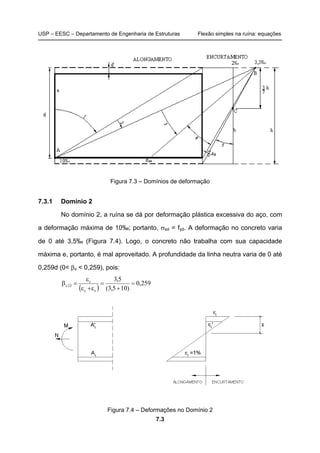
Este documento apresenta os conceitos fundamentais da flexão simples na ruína, incluindo hipóteses, diagramas de tensões, domínios de deformação e equações de equilíbrio. Exemplos ilustram o cálculo da altura útil, área de aço e detalhamento da seção para diferentes condições de carga e armadura.

1. FLEXÃO SIMPLES NA RUÍNA: EQUAÇÕES – CAPÍTULO 7
Libânio M. Pinheiro, Cassiane D. Muzardo, Sandro P. Santos.
12 maio 2003
FLEXÃO SIMPLES NA RUÍNA: EQUAÇÕES
7.1 HIPÓTESES
No dimensionamento à flexão simples, os efeitos do esforço cortante podem
ser considerados separadamente. Portanto, será considerado somente o momento
fletor, ou seja, flexão pura.
Admite-se a perfeita aderência entre as armaduras e o concreto que as
envolve, ou seja, a deformação específica de cada barra da armadura é igual à do
concreto adjacente.
A resistência do concreto à tração é desprezada, ou seja, na região do
concreto sujeita à deformação de alongamento, a tensão no concreto é considerada
nula.
Nas peças de concreto submetidas a solicitações normais, admite-se a
validade da hipótese de manutenção da forma plana da seção transversal até o
estado limite último, desde que a relação abaixo seja mantida:
2
d
0
>
l
l0 → distância entre as seções de momento fletor nulo
d → altura útil da seção
Com a manutenção da forma plana da seção, as deformações específicas
longitudinais em cada ponto da seção transversal são proporcionais à distância até a
linha neutra.

2. USP – EESC – Departamento de Engenharia de Estruturas Flexão simples na ruína: equações
7.2
7.2 DIAGRAMA DE TENSÕES NO CONCRETO
Permite-se substituir o diagrama parábola-retângulo pelo retangular, com
altura y = 0,8x e tensão σc = 0,85fcd = 0,85fck/γc, exceto nos casos em que a seção
diminuir a partir da linha neutra no sentido da borda mais comprimida. Nestes casos,
σc = 0,95 . 0,85fcd ≈ 0,80fcd. Os diagramas de tensões e alguns tipos de seção
encontram-se nas Figuras 7.1 e 7.2, respectivamente.
2,0‰
0,85 f
0,85 f
0,80 f
ou
h
x
y = 0,8x
= 3,5‰εc
cd
cdcd
Figura 7.1 – Diagrama de tensões
= 0,85fσ = 0,85fσ = 0,80fσ = 0,80fσcd cd cd cd cd cd cd cd
Figura 7.2 – Alguns tipos de seção e respectivas tensões, para diagrama retangular
7.3 DOMÍNIOS POSSÍVEIS
Na flexão, como a tração é resistida pela armadura, a posição da linha
neutra deve estar entre zero e d (domínios 2, 3 e 4), já que para x < 0 (domínio 1) a
seção está toda tracionada, e para x > d (domínio 4a e 5) a seção útil está toda
comprimida. Os domínios citados estão indicados na Figura 7.3.

3. USP – EESC – Departamento de Engenharia de Estruturas Flexão simples na ruína: equações
7.3
Figura 7.3 – Domínios de deformação
7.3.1 Domínio 2
No domínio 2, a ruína se dá por deformação plástica excessiva do aço, com
a deformação máxima de 10‰; portanto, σsd = fyd. A deformação no concreto varia
de 0 até 3,5‰ (Figura 7.4). Logo, o concreto não trabalha com sua capacidade
máxima e, portanto, é mal aproveitado. A profundidade da linha neutra varia de 0 até
0,259d (0< βx < 0,259), pois:
( )
259,0
)105,3(
5,3
sc
c
23x =
+
=
ε+ε
ε
=β
Figura 7.4 – Deformações no Domínio 2

4. USP – EESC – Departamento de Engenharia de Estruturas Flexão simples na ruína: equações
7.4
7.3.2 Domínio 3
No domínio 3, a ruína se dá por ruptura do concreto com deformação
máxima εc = 3,5‰ e, na armadura tracionada, a deformação varia de εyd até 10‰, ou
seja, o aço está em escoamento, com tensão σs = fyd (Figura 7.5).
É a situação ideal de projeto, pois há o aproveitamento pleno dos dois
materiais. A ruína é dúctil, pois ela ocorre com aviso, havendo fissuração aparente e
flechas significativas. Diz-se que as seção é subarmada. A posição da linha neutra
varia de 0,259d até x34 (0,259 < βx < βx34).
( ) )5,3(
5,3
ydsc
c
34x
ε+
=
ε+ε
ε
=β ;
s
yd
yd
E
f
=ε
cuε
sε
cuε
sεε <
d
x
yd < 10‰
= 3,5‰
Figura 7.5 – Deformações no Domínio 3
7.3.3 Domínio 4
Assim como no domínio 3, o concreto encontra-se na ruptura, com
εc = 3,5‰. Porém, o aço apresenta deformação abaixo de εyd e, portanto, ele está
mal aproveitado. As deformações podem ser verificadas na Figura 7.6.
O dimensionamento nesse domínio é uma solução antieconômica, além de
perigosa, pois a ruína se dá por ruptura do concreto e sem escoamento do aço. É
uma ruptura brusca, ou seja, ocorre sem aviso. Quando as peças de concreto são
dimensionadas nesse domínio, diz-se que elas são superarmadas, devendo ser
evitadas; para isso pode-se usar uma das alternativas:

5. USP – EESC – Departamento de Engenharia de Estruturas Flexão simples na ruína: equações
7.5
• Aumentar a altura h, porque normalmente b é fixo, dependendo da
espessura da parede em que a viga é embutida;
• Fixar x como xlim34, ou seja, βx = βx34, e adotar armadura dupla;
• Outra solução é aumentar a resistência do concreto (fck).
sε sε εyd0 <
d
x
cuε
cuε = 3,5‰
<
Figura 7.6 – Deformações no Domínio 4
7.4 EQUAÇÕES DE EQUILÍBRIO
Para o dimensionamento de peças na flexão simples com armadura dupla
(Figura 7.7), considera-se que as barras que constituem a armadura estão
agrupadas, concentradas no centro de gravidade dessas barras.
= 3,5‰ε cdσ
sε
sε
R'
R
M
d'
A
A'
b
d
h
x
y = 0,8xs
d
s
s
c
s
'
c
Figura 7.7 - Resistências e deformações na seção

6. USP – EESC – Departamento de Engenharia de Estruturas Flexão simples na ruína: equações
7.6
As equações de equilíbrio de forças e de momentos são respectivamente:
Rc + R’s – Rs = 0
Md = γf x Mk = Rc (d - y/2) + R’s (d - d’)
As resultantes no concreto (Rc) e nas armaduras (Rs e R’s) são dadas por:
Rc = b y σcd = b . 0,8x . 0,85fcd = 0,68 bd βx fcd
Rs = As σs
R’s = A’s σ’s
Para diagrama retangular de tensões no concreto, tem-se que:
y = 0,8x → d – y/2 = d (1 - 0,8x/2d) = d (1 - 0,4βx)
Com esses valores, resultam as seguintes equações para armadura dupla:
0,68 bd βx fcd + A’s σ’s - As σ s = 0 (1)
Md = 0,68 bd² βx fcd (1 - 0,4βx) + A’s σ’s (d – d’) (2)
Para armadura simples, A’s = 0. As equações (1) e (2) resultam:
0,68 bd βx fcd - As σ s = 0 (1’)
Md = 0,68 bd² βx fcd (1 - 0,4 β x) (2’)
7.5 EXEMPLOS
A seguir apresentam-se alguns exemplos de cálculo de flexão simples.
7.5.1 Exemplo 1
Cálculo da altura útil (d) e da área de aço (As) para seção retangular.
a) Dados
Concreto C25, Aço CA-50, b = 30 cm, Mk = 210 kN.m, βx= βx23
( )
259,0
)105,3(
5,3
sc
c
23x =
+
=
ε+ε
ε
=β

7. USP – EESC – Departamento de Engenharia de Estruturas Flexão simples na ruína: equações
7.7
b) Equações de equilíbrio
0,68 bd βx fcd - As σ s = 0 (1’)
Md = 0,68 bd² βx fcd (1 - 0,4βx) (2’)
c) Cálculo de d (equação 2’)
)259,04,01(
4,1
5,2
d21,4 2
×−××0,259××30×0,68=1000×
d = 58,93 cm (h = 59+3 = 62 cm)
d) Cálculo de As (equação 1’)
0
15,1
50
A
4,1
5,2
259,093,583068,0 s =×−××××
As = 12,80 cm²
7.5.2 Exemplo 2
Idem exemplo anterior com βx = βx34.
a) Cálculo de βx34
( ) )5,3(
5,3
ydsc
c
34x
ε+
=
ε+ε
ε
=β
‰07,2
210000
15,1/50
E
f
s
yd
yd ===ε
628,0
)07,25,3(
5,3
34x =
+
=β
b) Cálculo de d (equação 2’)
)628,04,01(
4,1
5,2
628d21,4 2
×−××0,××30×0,68=1000×
d = 41,42 cm (h = 42+3 = 45 cm)

8. USP – EESC – Departamento de Engenharia de Estruturas Flexão simples na ruína: equações
7.8
c) Cálculo de As (equação 1’)
0
15,1
50
A
4,1
5,2
628,042,413068,0 s =×−××××
As = 21,81 cm²
7.5.3 Exemplo 3
Cálculo da altura útil (d) e da área de aço (As) para seção retangular.
a) Dados
Concreto C25, Aço CA-50, b = 30 cm, h = 45 cm, d = 42cm, Mk = 252 kN.m.
b) Cálculo de βx
Na equação (2’), supondo armadura simples:
Md = 0,68 bd² βx fcd (1 – 0,4βx)
)4,01(
4,1
5,2
423068,04,125200 xx
2
β×−×β×××=×
25704βx² - 64260βx + 35280 = 0
βx² - 2,5βx + 1,3725 = 0
βx = 0,814 (βx > βx34: Domínio 4)
βx = 1,686 (x > d, portanto descartado)
c) Conclusão
Como βx > βx34 , σ s < fyd (domínio 4): há solução melhor com armadura dupla.
7.5.4 Exemplo 4
Idem exemplo anterior, com Mk = 315 kN.m.

9. USP – EESC – Departamento de Engenharia de Estruturas Flexão simples na ruína: equações
7.9
a) Cálculo de βx (equação 2’)
Md = 0,68 bd² βx fcd (1 – 0,4βx)
)4,01(
4,1
5,2
423068,04,131500 xx
2
β×−×β×××=×
25704βx² - 64260βx + 44100 = 0
βx² - 2,5βx + 1,7157 = 0
∆ = (-2,5)² - 4 x1 x 1,7157 = -0,6128 < 0
b) Conclusão
Não há solução para armadura simples. Neste caso só é possível armadura
dupla (exemplo 5).
7.5.5 Exemplo 5
Solução do exemplo anterior com armadura dupla.
a) Dados
Mk = 315 kN.m, βx = βx34 = 0,628, d’ = 3 cm
b) Cálculo de A’s (Equação 2)
Md = 0,68 bd² βx fcd (1 - 0,4βx) + A’s σ’s (d – d’)
1,4. 31500 = 0,68. 30. 422
. 0,628. 2,5/1,4 (1 - 0,4. 0,628) +A’s 50/1,15. (42–3)
A’s = 8,19 cm²
c) Cálculo de As (equação 1)
0,68 bd βx fcd + A’s σ’s - As σs = 0
0,68 . 30 . 42 . 0,628 . 2,5/1,4 + 8,19 . 50/1,15 - As . 50/1,15 = 0
As = 30,29 cm²

10. USP – EESC – Departamento de Engenharia de Estruturas Flexão simples na ruína: equações
7.10
d) Armaduras possíveis
As : 6 Ø 25 (Ase = 30 cm²) 2 camadas
8 Ø 22,2 (Ase = 31,04 cm²) 2 camadas
A’s : 2 Ø 25 (Ase = 10 cm²)
3 Ø 20 (Ase = 9,45 cm²)
f) Solução adotada (Figura 7.8)
Figura 7.8 – Detalhamento da seção