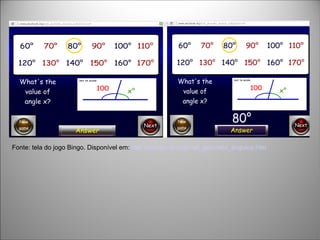
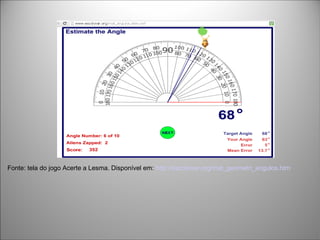
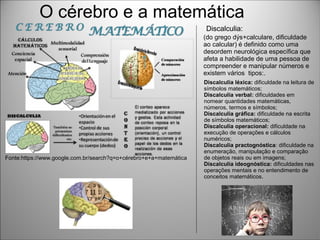
O documento discute como o professor pode auxiliar no aprendizado da matemática utilizando novas tecnologias como jogos e softwares, além de materiais concretos. Também aborda como o cérebro processa a matemática e possíveis dificuldades como a discalculia.

1. UNIVERSIDADE FEDERAL DE PELOTAS
CENTRO DE ENSINO A DISTÂNCIA
LICENCIATURA EM MATEMÁTICA A DISTÂNCIA
EIXO RECUPERAÇÃO PARALELA
Michelle Ternus dos Santos.
Matheus Santos Oliveira
Juarez H. Lima Junior
Polo Sapiranga.
Novas Tecnologias e Educação:A mediação do Professor.
O Cérebro e a Matemática

2. O professor pode ser considerado o grande responsável do
gostar ou não gostar de Matemática em sala de aula. O uso
de TIC’s (Tecnologia da Informação e Comunicação) auxilia
muito na vontade de aprender do aluno. Jogos, materiais
concretos, softwares e vontade do professor ensinar, são
peças fundamentais para o desenvolvimento de um bom
trabalho e um aprendizado significativo. Como diz Paulo
Freire: “Não se pode falar de educação sem amor”. O
presente trabalho trata justamente dessa mediação do
professor frente as mudanças. Também trata da relação
cérebro – matemática... como se desenvolve e curiosidades
acerca desse tema.
Introdução

3. Assistir ao vídeo do link abaixo,para entender sobre o que é e a importância do
saber ensinar em meio a tantas coisas novas. O princípio fundamental é o saber
aprender primeiro.
https://www.youtube.com/watch?v=XdY57PMsTsQ

4. O Jogo como nova tecnologia de
Ensino...
O jogo na escola não algo novo, ele é utilizado em todas as áreas do conhecimento, porém
devemos ter alguns cuidados no momento da escolha ou da elaboração, pois um jogo
quando bem elaborado ou bem estudado pelo docente, possibilita a construção do
conhecimento do aluno de uma forma significativa, fugindo do ensino tradicional. De
nada adianta aplicar um jogo por aplicar, tem que ser muito bem pensado o objetivo
dele. Segundo os PCN's (2006):
Recursos didáticos como jogos, livros, vídeos,
calculadoras, computadores e outros materiais têm
um papel importante no processo de ensino e
aprendizagem. Contudo, eles precisam estar
integrados a situações que levem ao exercício da
análise e da reflexão, em última instância, a base da
atividade matemática. (BRASIL, 2006, p. 19).
O docente deve usar essa ferramenta afim de amenizar e até extinguir as dificuldades dos
alunos em relação a tão temida matemática. Medo esse que muitas vezes vem dos pais
falarem que não gostam da matéria e de é muito difícil. Taxada pra alguns até como
impossível.
Conforme Borin (1996): “Outro motivo para a introdução de jogos nas aulas de matemática é a
possibilidade de diminuir bloqueios apresentados por muitos de nossos alunos que temem a
Matemática e sentem-se incapacitados para aprendê-la.”.

5. O material concreto funciona?
Alguns fatores que auxiliam a chegarmos a conclusão que funciona sim. São eles:
Elaboração de um plano de aula adequado à turma.
Acompanhamento docente ao raciocínio do aluno.
Adaptação do material concreto ao conteúdo matemático, por mais abstrato que este
pareça.
Saber exatamente o que almeja que seja absorvido pelo discente, focar nos objetivos da
aula.
Muitos alunos discutem entre si, questionam e até competem uns com os outros. E essa
comunicação, ou barulho, que alguns professores interpretam como bagunça, é fundamental
para que não seja criado um modelo de aluno como descreve Toffler (1981), um indivíduo
capaz de seguir ordens com atenção, não questionador, capaz de fazer algo sem se
preocupar ou interrogar por que é feito desse modo e não de outro, sempre confiante em que
há alguém que já pensou por ele como fazer. Definitivamente, não se quer esse tipo de
cidadão e profissional para o mundo e essa é uma responsabilidade do professor.

6. Um bom exemplo de Material
concreto...
Algeplan
Consiste em um material concreto, que pode ser feito de EVA,pode ser confeccionado
também em madeira e também há versões virtuais do mesmo, como a disponível em
http://mdmat.mat.ufrgs.br/algeplan/algeplan.swf. Se a intenção for mexer com o lado palpável
e concreto da matemática é melhor optar pelo EVA ou madeira.
Fonte: foto tirada do material confeccionado para o Projeto Jogos e Mídias digitais no Reforço Escolar. Aplicado na
escola 28 de fevereiro, em Sapiranga- RS no mês de novembro de 2013.

7. Algeplan para ensinar Álgebra
Quadrado de lado x, área x² e perímetro 4x – cor amarela
Quadrado de lado y, área y² e perímetro 4y – cor azul
Quadrado de lado 1, área 1² e perímetro 4 – cor vermelho
Retângulo de lados x e y, área xy e perímetro 2(x+y) – cor rosa
Retângulo de lado x e 1, área x e perímetro 2(x+1) – cor roxa
Retângulo de lado y e 1, área y e perímetro 2(y+1) – cor verde
Possui também figuras do mesmo tamanho das coloridas, na cor preta para representar o
negativo.
Fonte: foto tirada dos alunos manipulando Algeplan na Adição e subtração de Polinômios, durante o Projeto Jogos e Mídias
digitais no Reforço Escolar. Aplicado na escola 28 de fevereiro, em Sapiranga- RS no mês de novembro de 2013.

8. Fonte: foto tirada dos alunos manipulando Algeplan na multiplicação de Polinômios, durante o Projeto Jogos e Mídias
digitais no Reforço Escolar. Aplicado na escola 28 de fevereiro, em Sapiranga- RS no mês de novembro de 2013.
Fonte: foto tirada dos alunos manipulando Algeplan na multiplicação de Polinômios, durante o Projeto Jogos e Mídias
digitais no Reforço Escolar. Aplicado na escola 28 de fevereiro, em Sapiranga- RS no mês de novembro de 2013.

9. Baralho e dados para ensinar
Multiplicação e operações com números
positivos e negativos
Fonte: foto tirada da manipulação do jogo de baralho e dados, utilizado durante o Projeto Jogos e Mídias digitais no Reforço
Escolar. Aplicado na escola 28 de fevereiro, em Sapiranga- RS no mês de novembro de 2013.

10. Este material pode ser confeccionado
de uma forma mais barata ainda e em
conjunto com a disciplina de artes
Molde de dado. Disponível em
http://www.comofazer.com.br/como-
fazer-um-dado/
Baralho confeccionado em sala de aula. Disponível
em:http://educavalebahia.blogspot.com.br/2011/09/
planaltino-em-foco.html

11. O uso de software é eficaz?
Esta é outra questão que vêm à mente dos professores que desejam inovar suas aulas, mas
ainda tem a insegurança se realmente dará certo. A resposta é sim. Mas como toda
ferramenta que foge do tradicional, deve ser muito bem acompanhada pelo professor, pois o
computador permite ainda mais fuga de raciocínio ou distrações. Várias vezes durante uma
aula que esteja sendo utilizado o recurso da informática, o aluno pode ser chamado atenção
por estar no email pessoal, por estar jogando outro jogo que não traga o aprendizado que se
deseja naquela aula.
O uso de informática nas aulas de matemática é importante inclusive para aproximar o aluno
à matéria, pois é uma ferramenta com que já estão bem familiarizados, que tem interesse, e
transforma o método tradicional em algo que é bem aproveitado pelos discentes. Durante o
próprio desenrolar da aula é possível que sejam feitas pesquisas sobre determinado assunto,
apenas complementando, somando ideias. Segundo Borba (2001), em um momento do seu
discurso diz:
Eu gosto de pensar que a informática não melhora e nem
piora o ensino, ela transforma o ensino e transforma a
aprendizagem e ela transforma a forma como as pessoas
produzem conhecimento /.../ A gente vê que a utilização
da informática possibilita que argumentos visuais sejam
utilizados com muito mais frequência, porque é uma
característica da mídia informática.

12. Já para Haetinger (2003, p. 22) o uso de computadores e softwares pode ser comparado com os
livros, que podem ser ou não ser bem aproveitados, depende da postura e colocação do mestre
aos seus alunos, de sua condução inclusive de instigar a exploração de todas as possibilidades
que um determinado software ofereça:
Os softwares podem ser utilizados em sala de aula de modo
diferente ao proposto pelos fabricantes dos mesmos, criando-
se novos caminhos para exploração destes recursos,
adequando-os a cada realidade para obtermos maior
interatividade e resultados, aproximando-os de nossas
comunidades. É como no ensino presencial: quando usamos
um livro em sala de aula, ele pode ser apenas lido, ou
integrado a outras atividades. O computador e seus aplicativos
devem ser encarados de forma aberta, explorando-se todas as
possibilidades laterais, olhando-se as “entrelinhas” para
oferecermos aos alunos novas alternativas.
O aprendizado do aluno depende bastante do que se considera um fator muito importante: A
forma como o docente conduz a aula e a certeza do que quer ensinar. Se isso não estiver
bem planejado, então o software torna-se algo obsoleto, objeto de distração ou simplesmente
um passatempo de um período ou dois. O que confirma Betts (1998):
Não podemos isolar a tecnologia do conjunto da prática
educativa, porque, por si só, é burra. Existe a necessidade de
intervenção de uma ação docente para que ocorra a construção
do conhecimento. Nós, seres humanos, somos por natureza
seres aprendentes e, conscientemente ou não, os facilitadores
da construção do nosso próprio conhecimento.

13. Softwares para ensinar ângulos
Fonte: tela do jogo Bingo. Disponível em: http://escolovar.org/mat_geometri_angulos.htm

14. Fonte: tela do jogo Bingo. Disponível em: http://escolovar.org/mat_geometri_angulos.htm

15. Fonte: tela do jogo Encontre a Banana. Disponível em: http://escolovar.org/mat_geometri_angulos.htm

16. Fonte: tela do jogo Acerte a Lesma. Disponível em: http://escolovar.org/mat_geometri_angulos.htm

17. O cérebro e a matemática
Fonte:https://www.google.com.br/search?q=o+cérebro+e+a+matemática
Discalculia:
(do grego dýs+calculare, dificuldade
ao calcular) é definido como uma
desordem neurológica específica que
afeta a habilidade de uma pessoa de
compreender e manipular números e
existem vários tipos:.
Discalculia léxica: dificuldade na leitura de
símbolos matemáticos;
Discalculia verbal: dificuldades em
nomear quantidades matemáticas,
números, termos e símbolos;
Discalculia gráfica: dificuldade na escrita
de símbolos matemáticos;
Discalculia operacional: dificuldade na
execução de operações e cálculos
numéricos;
Discalculia practognóstica: dificuldade na
enumeração, manipulação e comparação
de objetos reais ou em imagens;
Discalculia ideognóstica: dificuldades nas
operações mentais e no entendimento de
conceitos matemáticos.

18. Curiosidade: Um pequeno estímulo elétrico no cérebro é capaz de melhorar as habilidades
matemáticas das pessoas por até seis meses sem afetar outras habilidades cognitivas.
Segundo a equipe liderada pelo Dr. Roi Cohen Kadosh, os estímulos elétricos não vão tornar seu
cérebro como o de Albert Einstein, mas a técnica poderia ajudar as pessoas a lidarem melhor com
matemática.
Fontes:
http://info.abril.com.br/noticias/ciencia/choque-no-cerebro-amplia-aptidao-matematica-05112010-21.shl e
http://www.enscer.com.br/material/brinquedos/justifica/contcalc.html
Contagem: As neurociências têm mostrado que os processos de contar e calcular são suportados
por circuitos neurais semelhantes entre si, mas distintos daqueles envolvidos na produção e
compreensão da linguagem. O contar começa a ser entendido como um processo de coordenação
motora dos atos de localizar e apontar ou marcar os objetos de interesse, e um processo neural de
quantificação dos objetos assim identificados.
O cálculo aritmético é um processo neural complexo, que envolve várias etapas Identificação:
nesta etapa, temos que reconhecer os argumentos do cálculo e o tipo de operação a realizar
Quantificação: associamos, nesta etapa, os elementos identificados pelo I aos Quantificadores
Proporcionais e Seqüenciais. Operação e recodificação.
Leia mais uma curiosidade em:
http://www.ciencia-online.net/2014/05/lesao-cerebral-genio-matematica.html que trata de
um homem que desenvolveu habilidades matemáticas após lesão no cérebro
Fluxo Sanguíneo Cerebral (CBF) durante uma tarefa de ativação mental. O
sujeito controle normal, linha de base (esquerda) e tarefa matemática (direita).
Nesse indivíduo, o aumento da perfusão durante as tarefas matemáticas é
visível tanto na área frontal inferior e parietal esquerda.
Fonte: Villanueva-Meyer et. cols. - Alasbimn Journal

19. Conclusão
Os principais pontos chaves que os educadores devem ter em mente é que: O que é pra um
nem sempre serve para todos. O aluno é único. E por fim, que ele está na sala de aula para
ensinar, é sua profissão, e como qualquer outra, tem que ser bem feita com efetividade,
competência e amor! Saber reconhecer o aluno, respeitando seus limites e seu tempo.
O professor é o grande responsável pelo sucesso ou fracasso das aulas que fogem do vício
de quadro – giz – caderno. Haetinger (2003) afirma que é importante ter esta fronteira de que o
computador, a televisão, o DVD, os jogos com dinâmicas, podem sim melhorar a compreensão do
aluno na sala de aula, todos são ferramentas didáticas pra esse fim, ou seja, elas auxiliam, mas
dependem de um professor capacitado pra que ela possa ser uma ferramenta que seja usada para
esse fim.
Concluímos que o professor deve adaptar-se as novas tecnologias para poder fazer a
mediação do aluno com o conhecimento, ensiná-lo a buscar informações, a fazer pesquisa e criar
os conceitos e conhecimentos necessários para desenvolver um aprendizado eficaz.
Cada parte do cérebro é responsável pelo desenvolvimento em matemática. Então os
docentes não podem passar por cima disso e ignorar como se todos funcionassem da mesma
forma, pois existem muitos problemas de aprendizado como a discalculia que atinge cerca de
6% da população mundial.

20. Bibliografia
BRASIL. Ministério da Educação, Secretaria de Educação Básica. Orientações Curriculares para o
Ensino Médio: Ciências da Natureza, Matemática e suas Tecnologias. Brasília: Ministério da
Educação, Secretaria de Educação Básica, v.2, 2006.
BORBA, M. C.; PENTEADO, M. G. Informática e Educação Matemática. Belo Horizonte: Autêntica,
2001 (Coleção Tendências em Educação Matemática).
BETTS, Davi Nelson. Novos paradigmas para a educação. Revista do Cogeime, v.13, 1998.
HAETINGER, Max. Informática na educação – um olhar criativo. São Paulo: Papirus, 2003.
TOFFLER, A. Choque do futuro. Lisboa: Livros do Brasil. 1981.
http://info.abril.com.br/noticias/ciencia/choque-no-cerebro-amplia-aptidao-matematica-
05112010-21.shl
http://www.enscer.com.br/material/brinquedos/justifica/contcalc.html
http://www.cerebromente.org.br/n11/mente/eisntein/rats-p.html