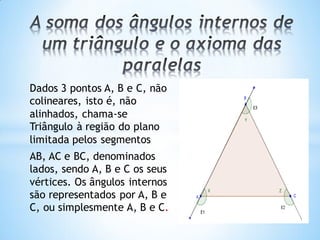
1. Dados 3 pontos A, B e C, não
colineares, isto é, não
alinhados, chama-se
Triângulo à região do plano
limitada pelos segmentos
AB, AC e BC, denominados
lados, sendo A, B e C os seus
vértices. Os ângulos internos
são representados por A, B e
C, ou simplesmente A, B e C.

2. Na figura acima, teremos então:
Soma dos ângulos internos: x + y + z = 180º
Soma do ângulos externos: E1 + E2 + E3 = 360º
Em todo triângulo, um ângulo externo é igual à
soma dos ângulos internos não adjacentes, ou
seja:
E1 = y + z
E2 = x + y
E3 = x + z

3. Vamos provar as três propriedades
acima:
A primeira é imediata, a partir da observação
atenta da figura abaixo, se lembrarmos que os
ângulos alternos internos possuem a mesma
medida. Assim, x = m e y = n. E como sabemos
que z + m + n = 180º, vem finalmente: x + y + z
= 180º

4. Para provar a segunda, basta observar que x + E1 = z + E2
= y + E3 = 180º.
Logo, podemos escrever: (x + E1 ) + ( z + E2 ) + ( y + E3 ) =
180º + 180º + 180º
Arrumando convenientemente, vem:
x + y + z + E1 + E2 + E3 = 540º
E como x + y + z = 180º , substituindo, vem:
180º + E1 + E2 + E3 = 540º
De onde finalmente tiramos: E1 + E2 + E3 = 360º
Para provar a terceira, observe que podemos escrever:
x + y + z = 180º = x + E1, de onde tiramos: E1 = y + z. Os
outros casos, são análogos.

5. Outra propriedade importante dos triângulos é que a
medida de qualquer lado é menor que a soma das medidas
dos outros dois.
Sendo a , b e c as medidas dos lados de um triângulo
qualquer, teremos sempre:
a<b+c
b<a+c
c<a+b
conhecidas como Desigualdades Triangulares.
DICA: se um triângulo possui dois lados medindo a e b, o
terceiro lado estará compreendido entre |a - b| e (a + b).
Assim, por exemplo, se um triângulo possui dois lados de
medidas 10 e 30, o terceiro lado estará compreendido
entre 30-10 e 30+10, ou seja, entre 20 e 40.

6. Os triângulos podem ser classificados
quanto à medida dos lados em:
EQUILÁTEROS: medidas
dos lados iguais; como
consequência disto , os
3 ângulos internos de
um triângulo
equilátero são
congruentes, isto é,
possuem a mesma
medida e, portanto
cada ângulo mede 60°.

7. ISÓSCELES: possuem
dois lados com medidas
iguais. O terceiro lado
chama se base.
Verifica-se facilmente,
que os ângulos da base
de um triângulo
isósceles possuem
medidas iguais, ou seja,
são congruentes.

8. ESCALENO: possui os três
lados desiguais.
Infere-se , portanto, que
todo triângulo equilátero
é isósceles, o que
significa que o conjunto
de todos os triângulos
equiláteros é um
subconjunto do conjunto
de todos os triângulos
isósceles

9. Os triângulos podem ser classificados
quanto às medidas dos ângulos internos,
em:
RETÂNGULO: possuem um ângulo reto ( 90° ).
O lado oposto ao ângulo reto é chamado
hipotenusa e os outros 2 lados, são chamados
catetos.

10. ACUTÂNGULO: todos os ângulos são agudos
OBTUSÂNGULO: possui um ângulo obtuso

11. Elementos lineares de um triângulo
Mediana - é o segmento que une um vértice ao ponto
médio do lado oposto. Conclui-se que todo triângulo
possui 3 medianas; o ponto de interseção das 3
medianas de um triângulo, encontram-se em um
ponto denominado BARICENTRO ou CENTRO DE
GRAVIDADE do triângulo.

12. Altura - é o segmento que une um vértice ao
lado oposto (ou ao prolongamento deste),
sendo perpendicular a esse lado. As 3 alturas
de um triângulo passam por um mesmo ponto,
chamado ORTOCENTRO do triângulo.

13. Bissectriz interna - é o segmento que divide cada
ângulo interno do triângulo, em 2 ângulos iguais. As 3
bissectrizes internas de um triângulo passam por um
ponto chamado INCENTRO do triângulo. O incentro é
o centro da circunferência inscrita no triângulo, isto
é , da circunferência que tangencia os 3 lados do
triângulo.

14. Mediatriz - é a reta perpendicular ao lado, passando
pelo ponto médio do mesmo. As 3 mediatrizes de
qualquer triângulo passam por um mesmo ponto,
chamado CIRCUNCENTRO, que é o centro da
circunferência circunscrita ao triângulo, isto é, da
circunferência que passa pelos 3 vértices do
triângulo.