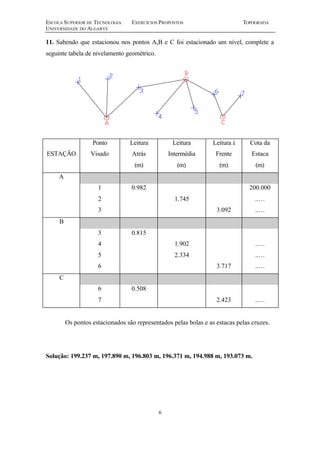
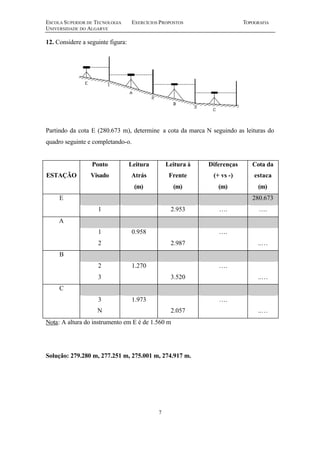
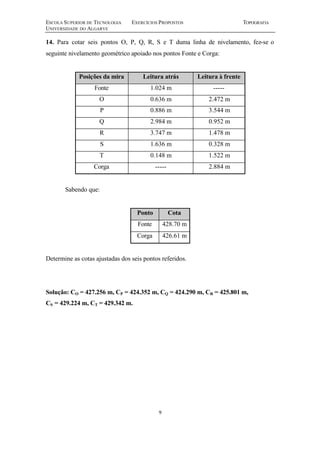
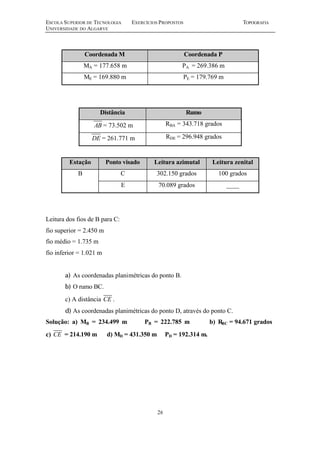
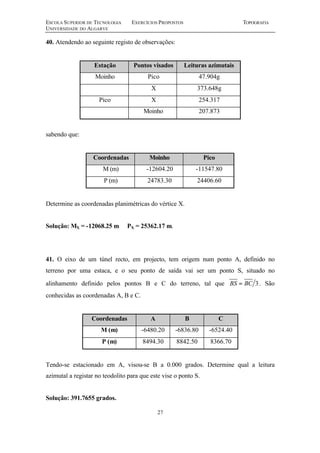
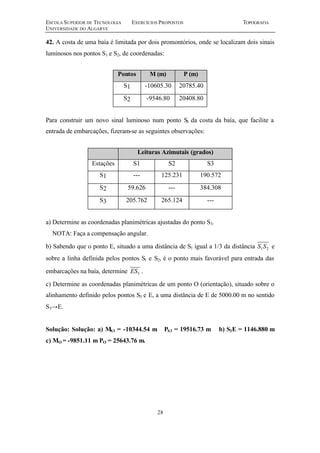
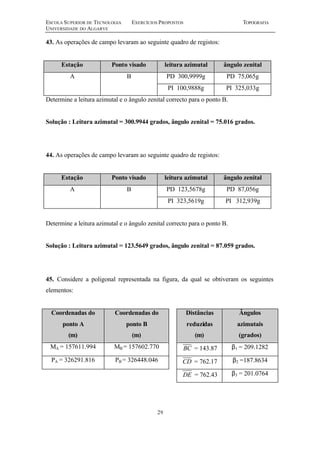
Este documento contém uma série de 20 exercícios de topografia sobre distâncias, escalas, altimetria, poligonais e nivelamento geométrico. Os exercícios abordam cálculos e problemas relacionados a medições topográficas com o objetivo de avaliar e aperfeiçoar os conhecimentos dos alunos sobre os principais tópicos da disciplina de topografia.