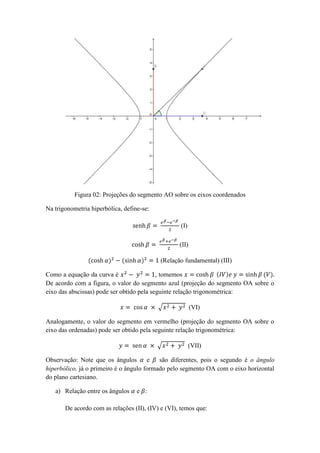
O documento aborda a transformação de radicais na forma polar utilizando a trigonometria hiperbólica, explicando conceitos relacionados a projeções em um gráfico. É apresentado como obter as projeções ortogonais de um ponto sobre a hipérbola e as relações entre ângulos na trigonometria hiperbólica. Além disso, o texto descreve a fórmula polar para raízes enésimas, demonstrando como expressões radicais podem ser simplificadas nessa forma.

1. FORMA POLAR DE UM RADICAL (INTRODUÇÃO)
Neste texto faremos uma abordagem sobre como transformar um radical do tipo:
na forma polar. Como o número
é real, usaremos a trigonometria
hiperbólica para obter a sua forma polar.
A trigonometria hiperbólica é baseada em uma hipérbole equilátera cuja equação é do
tipo:
e cujo gráfico é mostrado a seguir:
Figura 01: Hipérbole equilátera, centrada na origem.
Tomando um ponto A qualquer sobre a curva desta equação, podemos obter as
projeções ortogonais nos eixos “x” e “y” e seus respectivos valores, de acordo com
figura abaixo:

2. Figura 02: Projeções do segmento AO sobre os eixos coordenados
Na trigonometria hiperbólica, define-se:
(I)
(II)
(Relação fundamental) (III)
Como a equação da curva é
, tomemos
De acordo com a figura, o valor do segmento azul (projeção do segmento OA sobre o
eixo das abscissas) pode ser obtido pela seguinte relação trigonométrica:
(VI)
Analogamente, o valor do segmento em vermelho (projeção do segmento OA sobre o
eixo das ordenadas) pode ser obtido pela seguinte relação trigonométrica:
(VII)
Observação: Note que os ângulos
e
são diferentes, pois o segundo é o ângulo
hiperbólico, já o primeiro é o ângulo formado pelo segmento OA com o eixo horizontal
do plano cartesiano.
a) Relação entre os ângulos
e :
De acordo com as relações (II), (IV) e (VI), temos que:

3. (II)
(IV)
(VI)
Igualando as três relações, obtemos que:
Isolando o valor de
, temos que:
(VII)
Como
Somando
, então:
aos dois membros da equação, temos:
Daí:
Substituindo em VII, vem:
Analogamente, podemos obter uma fórmula similar com a outra relação
trigonométrica:
Utilizando a trigonometria hiperbólica, é possível transformar qualquer radical
da forma
em uma forma “polar”, utilizando as próprias funções
trigonométricas hiperbólicas. Para tal feito, iremos definir a norma do radical
como sendo
quocientes:
. Além disso, vamos definir os seguintes

4. Observe que as duas relações satisfaz:
Como
. Assim, podemos dizer que:
, podemos dividir os dois membros desta equação por
:

Daí:
Isolando “r”, obtemos finalmente a expressão polar para o referido radical:
Ou simplesmente:
Onde:

5. RAÍZES ENÉSIMAS DE R
Neste tópico iremos determinar uma expressão polar para as raízes enésimas de
r, ou seja:
Baseada na fómula de Moivre dos números complexos, pode-se demonstrar que:
Ou simplesmente:
Onde:
Ou:
Este procedimento faz com que todo radical escrito na forma
pode ser
decomposto em uma soma de radicais simples. Observe os exemplos abaixo:
Exemplo 01: Determine o valor de
na forma polar.
Solução:
Seja
Observe que:
.
Cálculo da norma de r:
Cálculo de
e escreva o resultado

6. Cálculo da raiz:
Portanto, a fórmula polar de
Forma algébrica de “x”:
Portanto:
é: