O documento apresenta uma proposta de ensino sobre o Teorema de Pitágoras utilizando as demonstrações de Bháskara da Índia e dos chineses. Serão abordados os conceitos de álgebra e geometria desenvolvidos na China e Índia, com foco nas origens e demonstrações deste importante teorema.

2.  TEMA: Matemática na China e Índia.
 CONTEXTUALIZAÇÃO: História da Matemática;
Matemática na China e Índia; Teorema de Pitágoras;
Álgebra e geometria através de Bháskara; Relações entre
China e Índia.
 CONTEÚDO: Teorema de Pitágoras
 SÉRIE E NÍVEL SUGERIDOS: 9º Ano do ensino
Fundamental
 TEMPO PREVISTO: 10 (dez) Aulas de 50mim,
aproximadamente, cada aula.

3. MATERIAL NECESSÁRIO
Datashow e caixa de som
 Livro Didático
Quadro
 Papel e lápis
 Textos de Apoio
Material Concreto

4.  Desenvolver o pensamento numérico, ampliando e
construindo novos significados para os números e as
operações e o pensamento algébrico.
 Ampliar a discussão sobre o ensino de trigonometria
no triângulo retângulo no ensino fundamental a partir
das origens do desenvolvimento desses conceitos.

5. A história da matemática traz outra forma de ver e
entender esta disciplina, tornando-a mais prazerosa.
Favorece o conhecimento como um todo.
Todo o processo histórico e evolutivo da
matemática proporcionou ao homem interagir de forma
bastante visível com as situações do cotidiano. Tudo o
que foi desenvolvido dentro da matemática surgiu da
necessidade do homem em determinadas situações .
Trabalhar história da matemática com enfoque no
Teorema de Pitágoras e suas diferentes demonstrações
traz a proposta de levar ao aluno a entender o porquê e
como foi desenvolvido tal proposição.

6. Estudar o teorema de Pitágoras utilizando as
demonstrações de Bháskara, e demonstração chinesa
para o teorema. Podendo interligar geometria e álgebra
através de Bháskara, a quem geralmente se atribui
(indevidamente) a fórmula para se resolver equações do
segundo grau, apresentando sua construção para
justificar o teorema de Pitágoras, em que decompõe o
quadrado sobre a hipotenusa em quatro triângulos
congruentes mais um quadrado de lado igual à diferença
entre os catetos desse triângulo. Apresentar ao aluno que
muito tempo antes, essa demonstração também já fora
dada na China. Podendo relacionar as duas
demonstrações.

7.  1º momento: (Quatro Aulas) Atividades de introdução
do assunto que será abordado: teorema de Pitágoras.
Nesse momento o professor introduzirá o conteúdo,
apresentando aplicações desse teorema, origem do seu
nome e idealizador.
 Objetivos:
 Entender o que é um Teorema;
Conhecer a Biografia de Pitágoras de Samos;
Refletir sobre a “origem” do Teorema de Pitágoras;

8.  2º momento: (Duas Aula) Retomar o conteúdo do
primeiro momento, através de atividades que
permitirão a construção da lógica que servirá de
referência para a demonstração do teorema de
Pitágoras. Questionando os alunos como eles acham
que Pitágoras chegou a o seu teorema.
 Objetivos:
 Instigar a curiosidade discente a respeito da
demonstração do Teorema de Pitágoras.
 Demonstrar o Teorema de Pitágoras

9.  3º Momento: (Quatro Aulas) Atividades de
aprofundamento e ampliação do estudo do teorema de
Pitágoras a partir da demonstração feita por Baskara, nesse
momento introduz a demonstração feita pelos Chineses.
Deve-se pedir aos alunos que encontrem relações entre as
duas demonstrações.
 Objetivos:
 Demonstrar o Teorema de Pitágoras através do método de
Bhaskára;
 Demonstrar o Teorema de Pitágoras através do método
Chinês;
 Relacionar algebricamente ou geometricamente as duas
demonstrações;

10.  4º Momento: Avaliação.
 Objetivo:
 O tema será avaliado de forma contínua,
acompanhando o desenvolvimento pessoal e coletivo
da turma na resolução das atividades propostas,
individualmente ou em grupo.

11.  Estudar o teorema de Pitágoras utilizando as
demonstrações de Bháskara para o teorema de
Pitágoras.
 Utilizar a demonstração Chinesa desse teorema.
 Relacionas a demonstração de Bháskara e a
demonstração Chinesa do teorema.
 Criar uma demonstração do Teorema através de uma
figura dada.

15.  Atividade 1: A figura abaixo ilustra uma construção,
feita por Bhaskara, no século XII d.C, para justificar
uma propriedade do triângulo retângulo, conhecido e
estudado por nós como teorema de Pitágoras. Vamos
tentar entender como essa construção pode nos ajudar
a demonstrar o teorema de Pitágoras.

17.  1) Como é mesmo o teorema de Pitágoras?
 2) Quais são as figuras planas que formam a figura 1?
 3) Quais são as figuras planas que formam a figura 2?
 4) O que a figura 1 tem a ver com a figura 2? Explique.
 5) Quantos quadrados, no mínimo, você vê nas figuras
abaixo.
 6) Construa em papel as 5 figuras que compõe a figura 1.
 7) Monte essas figuras de modo a obter a figura 2. Explique
por que isso é possível.
 8) Se o lado maior do retângulo mede a cm e o menor b cm,
expresse, a partir de a e b :
 a) A medida da diagonal do retângulo.
 b) A medida do lado do quadrado maior.
 c) A medida do lado do quadrado menor.
 9) Chamando de c a medida da hipotenusa dos triângulos
retângulos, mostre que: 푎2 + 푏2 = 푐2

18.  Bhaskara (1114-1185) foi um matemático indiano que
encontrou uma demonstração para o teorema de Pitágoras.
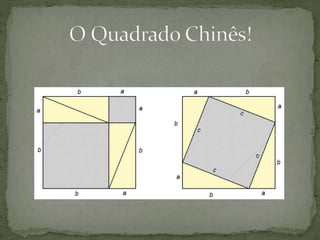
 Na figura, o quadrado [ABCD] está dividido em quatro
triângulos retângulos iguais e um quadrado. Desta divisão
surgem as seguintes relações:
 • AG = CH = DF = BE = c
 • AE = CG = DH = BF = b
 1. Por que é que a área de cada triângulo pode ser calculada
utilizando a expressão:
푏 푥 푎
2
 2. Mostra que:
 2.1. a área do quadrado [EFHG] é (b - c)2.
 2.2. a área do quadrado [ABDC] é 푏2 + 푐2

19.  GÊNIOS DO ORIENTE. A História da Matemática.
Episódio 2. Segundo episódio da série A História da
Matemática, uma produção da BBC e da Open
University que resume 30 mil anos de desenvolvimento
das ideias matemáticas que formam a base da nossa
cultura, ciência e tecnologia.
 Dicas Pedagógicas da Tv Escola. A HISTÓRIA DA
MATEMÁTICA. EPISÓDIO: GÊNIOS DO ORIENTE.