Baixado 58 vezes
Carregado porAlonso Patricio Nolasco
Percolação apresentação
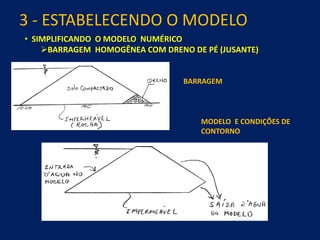
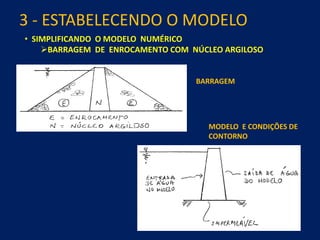
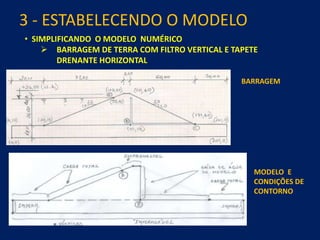
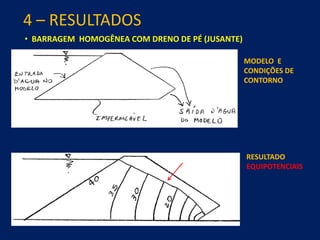
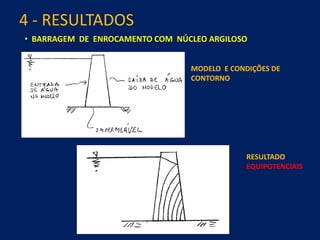
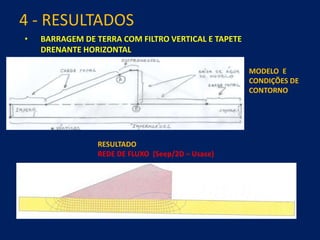
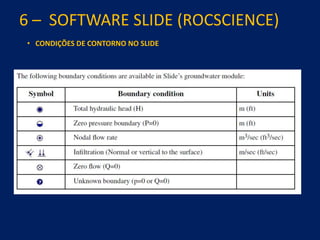
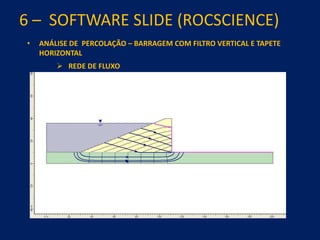
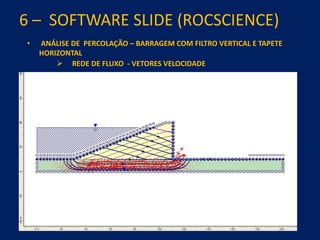
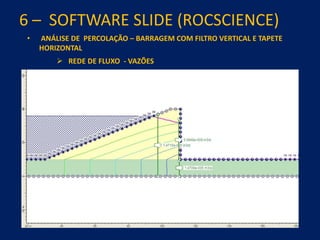
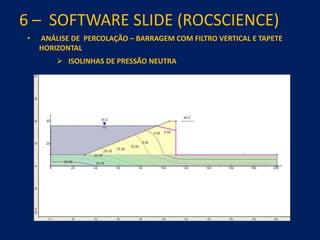
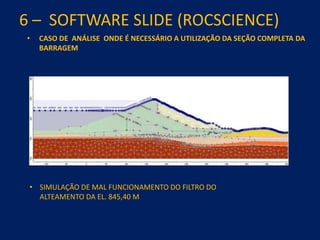
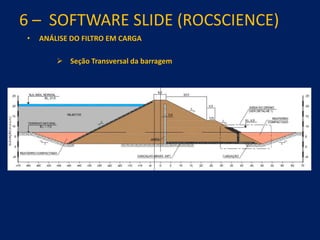
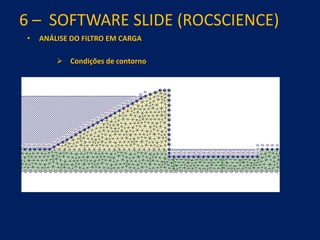
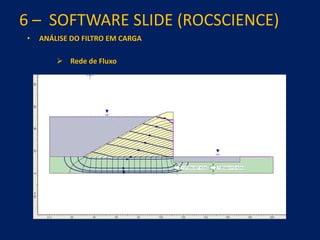
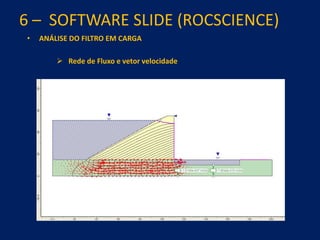
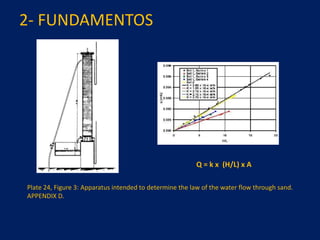
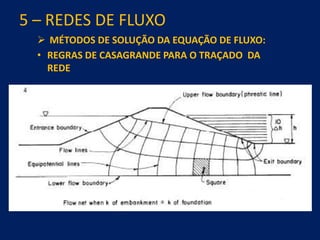
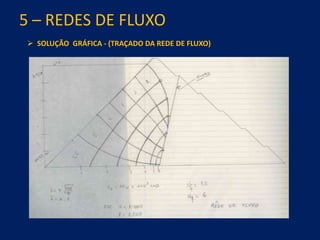
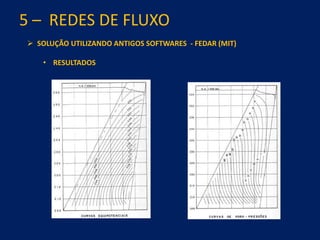
1) O documento discute aspectos práticos da modelagem numérica da percolação em barragens de terra e enrocamento, incluindo fundamentos, métodos de estabelecimento de modelos, resultados e recomendações. 2) É apresentada a equação geral de fluxo de Darcy e métodos de solução como redes de fluxo, análise analógica e elementos finitos. 3) O documento fornece recomendações para modelagem numérica simplificada como utilizar poucos elementos e focar nas partes essenciais da estrut
Percolação apresentação
- 1. PERCOLAÇÃO EM BARRAGENS DETERRA E ENROCAMENTO ASPECTOS PRÁTICOS DA MODELAGEM NUMÉRICA José Mário Q. Mafra, M.Sc. Julho/2011
- 2. OBSERVAÇÃO FUNDAMENTAL EM BARRAGENSDE TERRA E ENROCAMENTO A PERCOLAÇÃO É ESTUDADA CONSIDERANDO O SOLO SATURADO (DOMÍNIO DA MECÂNICA DOS SOLOS CLÁSSICA).
- 3. 1- OBJETIVOS • ESTUDARO MOVIMENTO DA ÁGUA NO INTERIOR DO MACIÇO; • ESTIMAR AS PRESSÕES DE ÁGUA NO INTERIOR DO MACIÇO (NECESSÁRIAS AO ESTUDO DA ESTABILIDADE DE TALUDES); • ESTIMAR SUB-PRESSÕES EM FUNDAÇÕES; • ESTIMAR A VAZÃO PERCOLADA ATRAVÉS DO MACIÇO (NECESSÁRIA AO DIMENSIONAMENTO DO SISTEMA DE DRENAGEM).
- 4. 2- FUNDAMENTOS Pierre Simon,Marquis de Laplace 1749 - 1827 EQUAÇÃO GERAL DE FLUXO
- 5. 2 - FUNDAMENTOS THEPUBLIC FOUNTAINS OF DIJON. APPENDIX - D. Determination of the laws of water flow through sand. Henry Darcy (1803 – 1858)
- 6. 2- FUNDAMENTOS Plate 24,Figure 3: Apparatus intended to determine the law of the water flow through sand. APPENDIX D. Q = k x (H/L) x A
- 7. 2- FUNDAMENTOS • SOLUÇÃOGRÁFICA DE FORCHHEIMER (1912) ESTABELECEU A SOLUÇÃO GRÁFICA PARA A REDE DE FLUXO
- 8. 2- FUNDAMENTOS • PARÁBOLADE KOSENY (1931) A LINHA DE FLUXO SUPERIOR SE APROXIMA DE UMA PARÁBOLA Solo de permeabilidade k apoiado em uma camada impermeável (k=0) e desaguando em um dreno com k =
- 9. 2- FUNDAMENTOS • OPROBLEMA DA ANISOTROPIA DOS SOLOS ARTIFÍCIO DE SAMSIOE (1930) Consiste em transformar a escala na qual se desenha a rede de fluxo, dividindo-se as distâncias horizontais por: A escala vertical continua a mesma; Sobre a figura deformada traça-se a rede de fluxo pelo processo gráfico apresentado (quadrângulos). Após a transformação, volta-se à escala original e redesenha-se a rede de fluxo que agora ficará com a malha deformada (deixam de ser quadrângulos e se transformam em losangos) .
- 10.
- 11. 2- FUNDAMENTOS As linhasde fluxo e equipotenciais são traçadas por tentativa e erro, e devem obedecer as seguintes condições (Arthur Casagrande, 1937): I) São normais entre si; II) As malhas são quadrangulares (é possível inscrever um círculo tangenciando os quatro lados da malha); III) Todas as superfícies de entrada e saída d'água são equipotenciais; IV) Toda superfície impermeável é uma linha de fluxo; V) As linhas freáticas (superfícies livres em contato com a pressão atmosférica) terão em cada ponto, o potencial determinado pela própria cota do ponto; Obedecendo-se as cinco regras acima, a solução é única, independente da habilidade individual para o desenho.
- 12. 3 - ESTABELECENDOO MODELO • SIMPLIFIQUE A GEOMETRIA DA ESTRUTURA; • MODELE SOMENTE AS PARTES ESSENCIAIS À SOLUÇÃO DO PROBLEMA (ISTO É, TRECHOS PERMEÁVEIS DA BARRAGEM NÃO DEVEM FAZER PARTE DO MODELO); • A ANÁLISE NUMÉRICA DE PERCOLAÇÃO EM BARRAGENS É FEITA NO DOMÍNIO DA MECÂNICA DOS SOLOS CLÁSSICA; • SEMPRE TENHA EM MENTE O MUNDO REAL.
- 13. 3 - ESTABELECENDOO MODELO • CONTRASTES DE PERMEABILIDADE > 102 cm/s CAUSAM INSTABILIDADE NUMÉRICA E RESULTADOS ERRADOS; • OS DRENOS EXISTEM FÍSICAMENTE, MAS NÃO NECESSITAM CONSTAR DO MODELO, POIS, A PERMEABILIDADE DO DRENO É, NA PRÁTICA, INFINITA () EM RELAÇÃO AO SOLO IMPERMEÁVEL ; • NÃO HÁ DESENVOLVIMENTO DE PRESSÃO NEUTRA EM MATERIAIS FRANCAMENTE DRENANTES; • INCLUA NO MODELO SOMENTE OS MATERIAIS QUE CONTRIBUEM PARA A QUEDA DE PRESSÃO.
- 14. 3 - ESTABELECENDOO MODELO • SIMPLIFICANDO O MODELO NUMÉRICO BARRAGEM HOMOGÊNEA COM DRENO DE PÉ (JUSANTE) BARRAGEM MODELO E CONDIÇÕES DE CONTORNO
- 15. 3 - ESTABELECENDOO MODELO • SIMPLIFICANDO O MODELO NUMÉRICO BARRAGEM DE ENROCAMENTO COM NÚCLEO ARGILOSO BARRAGEM MODELO E CONDIÇÕES DE CONTORNO
- 16. 3 - ESTABELECENDOO MODELO • SIMPLIFICANDO O MODELO NUMÉRICO BARRAGEM DE TERRA COM FILTRO VERTICAL E TAPETE DRENANTE HORIZONTAL BARRAGEM MODELO E CONDIÇÕES DE CONTORNO
- 17. 4 – RESULTADOS •BARRAGEM HOMOGÊNEA COM DRENO DE PÉ (JUSANTE) MODELO E CONDIÇÕES DE CONTORNO RESULTADO EQUIPOTENCIAIS PRESSÃO P= 0
- 18. 4 - RESULTADOS •BARRAGEM DE ENROCAMENTO COM NÚCLEO ARGILOSO MODELO E CONDIÇÕES DE CONTORNO RESULTADO EQUIPOTENCIAIS
- 19. 4 - RESULTADOS •BARRAGEM DE TERRA COM FILTRO VERTICAL E TAPETE DRENANTE HORIZONTAL MODELO E CONDIÇÕES DE CONTORNO RESULTADO REDE DE FLUXO (Seep/2D – Usace)
- 20. 4 - RESULTADOS •BARRAGEM DE TERRA COM NÚCLEO ARGILOSO BARRAGEM REDE DE FLUXO
- 21. 5 – REDESDE FLUXO O MUNDO REAL
- 22. 5 – REDESDE FLUXO MÉTODOS DE SOLUÇÃO DA EQUAÇÃO DE FLUXO: • MÉTODOS ANALÍTICOS - (EXATOS); • MÉTODOS ANÁLOGICOS - (ANALOGIA ELÉTRICA); • MÉTODOS NUMÉRICOS - (ELEMENTOS FINITOS, DIFERENÇAS FINITAS); • MODELOS FÍSICOS; • MÉTODOS GRÁFICOS;
- 23. 5 – REDESDE FLUXO MÉTODOS DE SOLUÇÃO DA EQUAÇÃO DE FLUXO: • MÉTODOS ANÁLOGICOS - (ANALOGIA ELÉTRICA);
- 24. 5 – REDESDE FLUXO MÉTODOS DE SOLUÇÃO DA EQUAÇÃO DE FLUXO: • MÉTODOS ANÁLOGICOS - (ANALOGIA ELÉTRICA);
- 25. 5 – REDESDE FLUXO MÉTODOS DE SOLUÇÃO DA EQUAÇÃO DE FLUXO: • MÉTODOS ANÁLOGICOS - (ANALOGIA ELÉTRICA);
- 26. 5 – REDESDE FLUXO MÉTODOS DE SOLUÇÃO DA EQUAÇÃO DE FLUXO: • MÉTODOS ANÁLOGICOS - (ANALOGIA ELÉTRICA);
- 27. 5 – REDESDE FLUXO MÉTODOS DE SOLUÇÃO DA EQUAÇÃO DE FLUXO: • REDE DE FLUXO SOLOS ISOTRÓPICOS - REDE DESENHADA NA ESCALA NATURAL; SOLOS ANISOTRÓPICOS - ESCALA TRANSFORMADA.
- 28. 5 – REDESDE FLUXO MÉTODOS DE SOLUÇÃO DA EQUAÇÃO DE FLUXO: • REDE DE FLUXO
- 29. 5 – REDESDE FLUXO MÉTODOS DE SOLUÇÃO DA EQUAÇÃO DE FLUXO: • REGRAS DE CASAGRANDE PARA O TRAÇADO DA REDE Resumo: 1 - Utilize um papel tamanho A4; 2 - Procurar estudar redes de fluxo já construídas; 3 – Usar poucos canais de fluxo (4 a 5 no máximo) nas primeiras tentativas de traçado da rede; 5 - “Acertar” a rede como um todo, deixando os detalhes para o final; 6 – As transições entre trechos retos e curvos das linhas devem ser suaves, em cada canal, o tamanho dos “quadrados” varia gradualmente. (1902 -1981)
- 30. 5 – REDESDE FLUXO MÉTODOS DE SOLUÇÃO DA EQUAÇÃO DE FLUXO: • REGRAS DE CASAGRANDE PARA O TRAÇADO DA REDE
- 31. 5 – REDESDE FLUXO MODELAGEM FÍSICA:
- 32. 5 – REDESDE FLUXO MODELAGEM FÍSICA:
- 33. 5 – REDESDE FLUXO MODELAGEM FÍSICA (Taylor, 1948):
- 34. 5 – REDESDE FLUXO SOLUÇÃO GRÁFICA - (TRAÇADO DA FREÁTICA)
- 35. 5 – REDESDE FLUXO SOLUÇÃO GRÁFICA - (TRAÇADO DA REDE DE FLUXO)
- 36. 5 – REDESDE FLUXO SOLUÇÃO GRÁFICA
- 37. 5 – REDESDE FLUXO SOLUÇÃO GRÁFICA
- 38. 5 – REDESDE FLUXO SOLUÇÃO UTILIZANDO ANTIGOS SOFTWARES - FEDAR (D0S)
- 39. 5 – REDESDE FLUXO SOLUÇÃO UTILIZANDO ANTIGOS SOFTWARES - FEDAR (MIT) • HIPÓTESE ADOTADA
- 40. 5 – REDESDE FLUXO SOLUÇÃO UTILIZANDO ANTIGOS SOFTWARES - FEDAR (MIT) • RESULTADOS
- 41. 6 – SOFTWARESLIDE (ROCSCIENCE) • CONDIÇÕES DE CONTORNO NO SLIDE
- 42. 6 – SOFTWARESLIDE (ROCSCIENCE) • ANÁLISE DE PERCOLAÇÃO – BARRAGEM COM FILTRO VERTICAL E TAPETE HORIZONTAL
- 43. 6 – SOFTWARESLIDE (ROCSCIENCE) • ANÁLISE DE PERCOLAÇÃO – BARRAGEM COM FILTRO VERTICAL E TAPETE HORIZONTAL CONDIÇÕES DE CONTORNO
- 44. 6 – SOFTWARESLIDE (ROCSCIENCE) • ANÁLISE DE PERCOLAÇÃO – BARRAGEM COM FILTRO VERTICAL E TAPETE HORIZONTAL CONDIÇÕES DE CONTORNO
- 45. 6 – SOFTWARESLIDE (ROCSCIENCE) • ANÁLISE DE PERCOLAÇÃO – BARRAGEM COM FILTRO VERTICAL E TAPETE HORIZONTAL REDE DE FLUXO
- 46. 6 – SOFTWARESLIDE (ROCSCIENCE) • ANÁLISE DE PERCOLAÇÃO – BARRAGEM COM FILTRO VERTICAL E TAPETE HORIZONTAL REDE DE FLUXO - VETORES VELOCIDADE
- 47. 6 – SOFTWARESLIDE (ROCSCIENCE) • ANÁLISE DE PERCOLAÇÃO – BARRAGEM COM FILTRO VERTICAL E TAPETE HORIZONTAL MALHA DE ELEMENTOS FINITOS E VAZÕES - (Seep/2D – Usace)
- 48. 6 – SOFTWARESLIDE (ROCSCIENCE) • ANÁLISE DE PERCOLAÇÃO – BARRAGEM COM FILTRO VERTICAL E TAPETE HORIZONTAL REDE DE FLUXO - VAZÕES
- 49. 6 – SOFTWARESLIDE (ROCSCIENCE) • ANÁLISE DE PERCOLAÇÃO – BARRAGEM COM FILTRO VERTICAL E TAPETE HORIZONTAL ISOLINHAS DE PRESSÃO NEUTRA
- 50. 6 – SOFTWARESLIDE (ROCSCIENCE) • CASO DE ANÁLISE ONDE É NECESSÁRIO A UTILIZAÇÃO DA SEÇÃO COMPLETA DA BARRAGEM • SIMULAÇÃO DE MAL FUNCIONAMENTO DO FILTRO DO ALTEAMENTO DA EL. 845,40 M
- 51. 6 – SOFTWARESLIDE (ROCSCIENCE) • CASO DE ANÁLISE ONDE É NECESSÁRIO A UTILIZAÇÃO DA SEÇÃO COMPLETA DA BARRAGEM • SIMULAÇÃO DE MAL FUNCIONAMENTO DO FILTRO DO ALTEAMENTO DA EL. 845,40 M • NOTAR QUE A LINHA FREÁTICA CORTA O FILTRO.
- 52. 6 – SOFTWARESLIDE (ROCSCIENCE) • CASO DE ANÁLISE ONDE É NECESSÁRIO A UTILIZAÇÃO DA SEÇÃO COMPLETA DA BARRAGEM • SIMULAÇÃO DE FUNCIONAMENTO DEFICIENTES DO FILTRO DO ALTEAMENTO DA EL. 845,40 M • NOTAR QUE A LINHA FREÁTICA CORTA O FILTRO. Praga Remanescente
- 53. 6 – SOFTWARESLIDE (ROCSCIENCE) • ANÁLISE DO FILTRO EM CARGA Seção Transversal da barragem
- 54. 6 – SOFTWARESLIDE (ROCSCIENCE) • ANÁLISE DO FILTRO EM CARGA Condições de contorno
- 55. 6 – SOFTWARESLIDE (ROCSCIENCE) • ANÁLISE DO FILTRO EM CARGA Rede de Fluxo
- 56. 6 – SOFTWARESLIDE (ROCSCIENCE) • ANÁLISE DO FILTRO EM CARGA Rede de Fluxo e vetor velocidade
- 57. 7 – RECOMENDAÇÕESFINAIS • “RULES OF THUMB” • USE O MENOR NÚMERO DE ELEMENTOS FINITOS POSSÍVEL. RARAMENTE SERÁ NECESSÁRIO UTILIZAR MAIS DE 1000 ELEMENTOS; • EM GERAL, TODOS OS ELEMENTOS DEVEM SER VISTOS A OLHO NÚ NA TELA COM 100% DE ZOOM E EM ESCALA 1V:1H; • NÃO INCLUA PARTE DA ESTRUTURA QUE NÃO SEJA SIGNIFICANTE PARA O COMPORTAMENTO DO MODELO; • LEMBRE-SE SEMPRE QUE O MODELO É UMA ABSTRAÇÃO DA CONFIGURAÇÃO GEOMETRICA REAL DA ESTRUTURA NO CAMPO.
- 58.
- 59. OBRIGADO PELA ATENÇÃO! J.M.Q. MAFRA