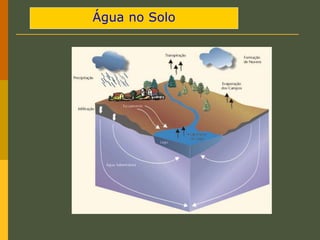
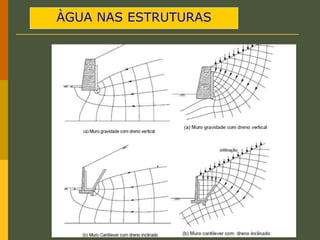
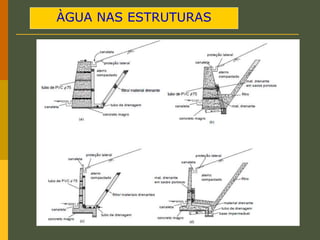
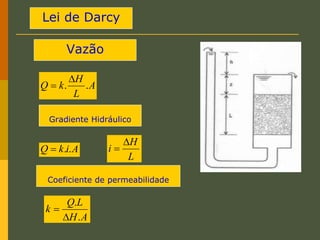
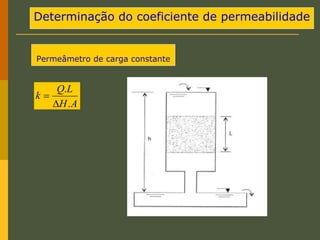
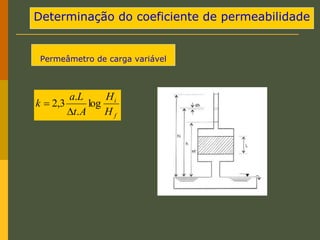
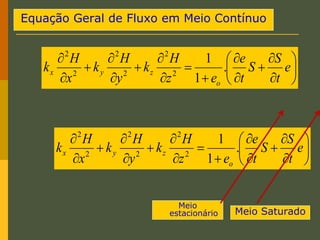
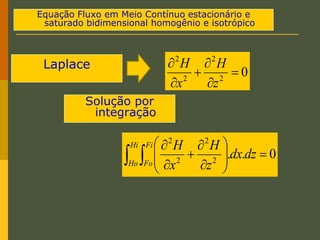
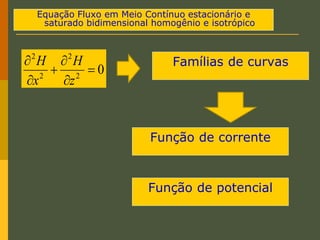
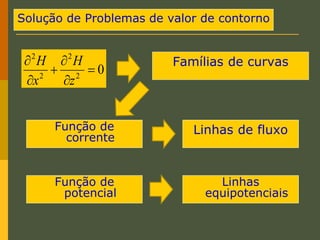
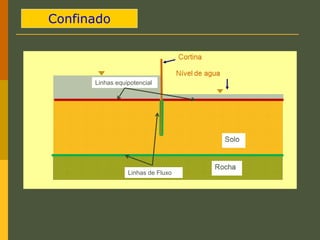
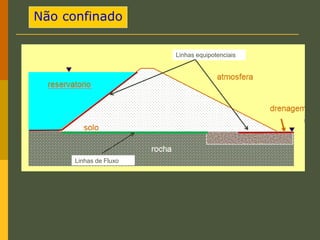
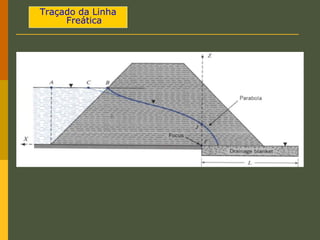
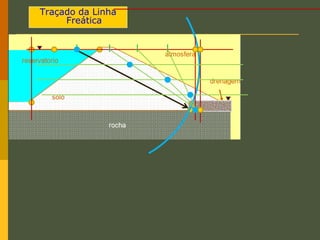
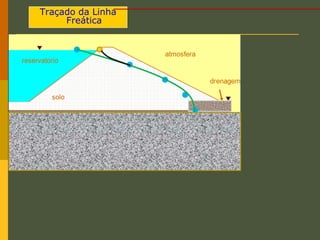
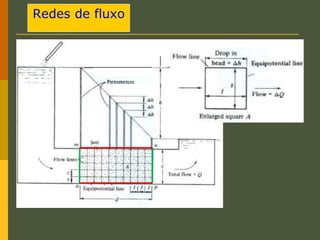
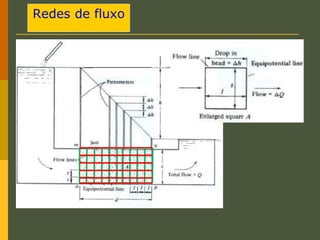
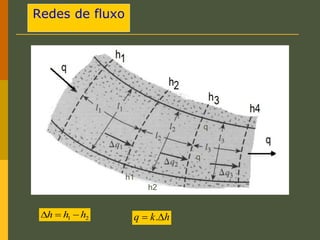
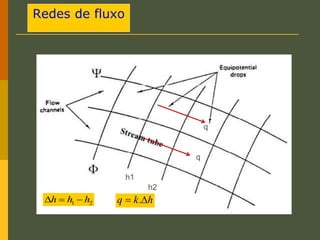
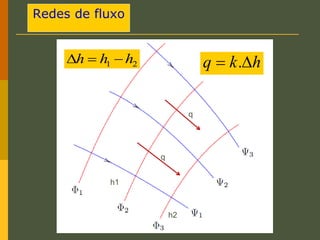
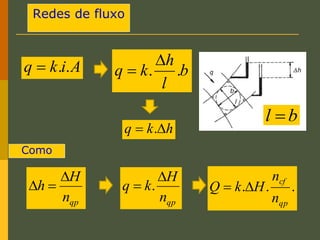
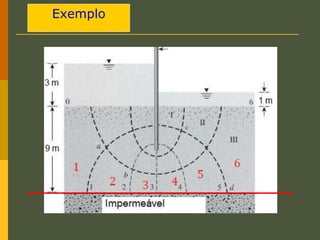
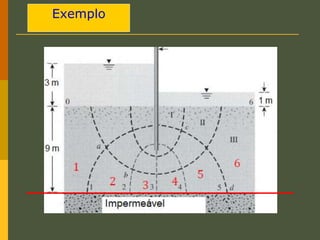
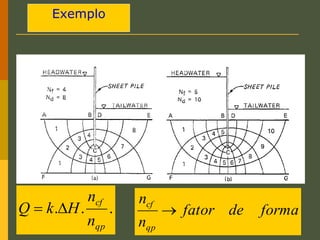
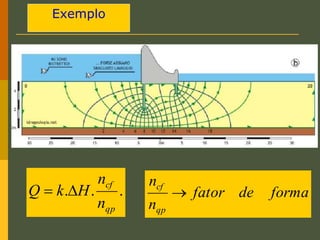
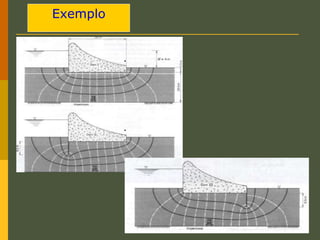
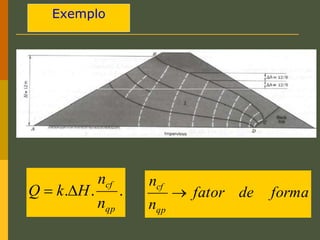
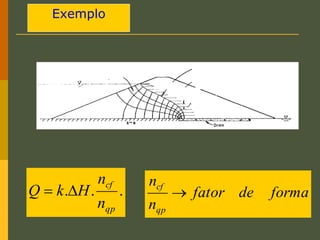
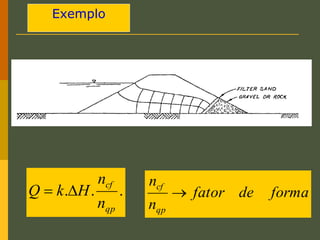
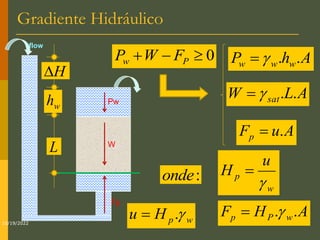
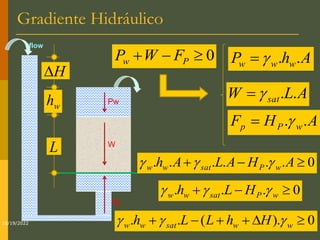
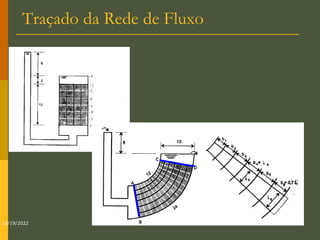
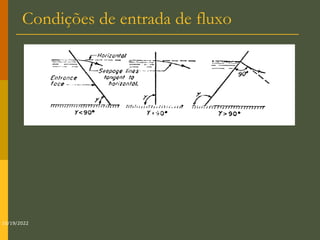
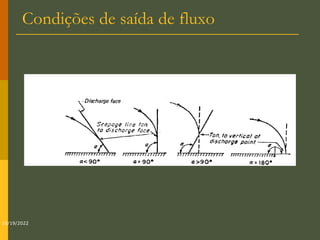
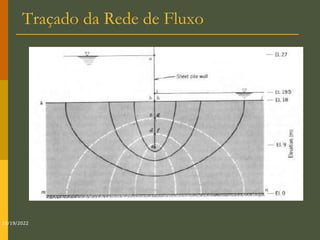
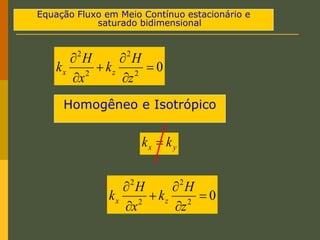
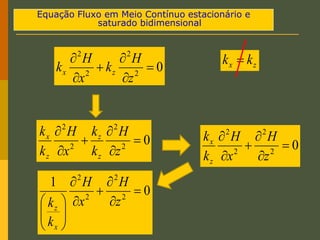
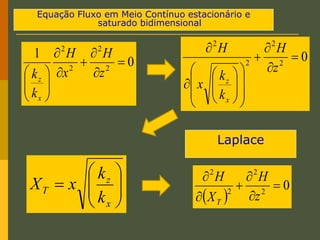
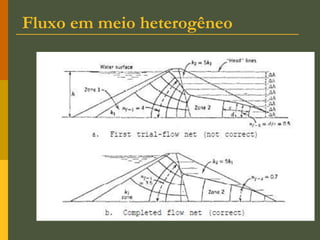
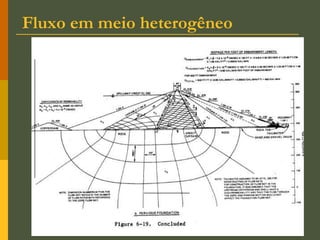
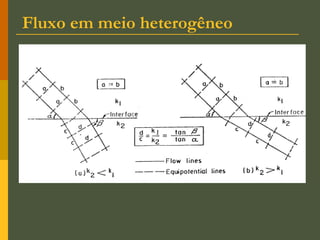
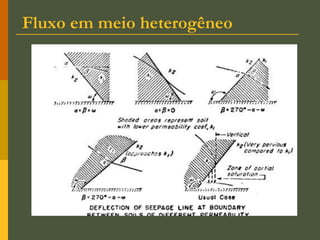
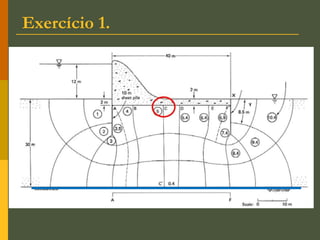
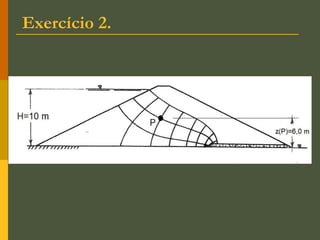
O documento discute os princípios da percolação de água no solo, incluindo a lei de Darcy, determinação do coeficiente de permeabilidade, equações de fluxo em meios contínuos saturados e não saturados, traçado da linha freática, e redes de fluxo. Aborda também fluxo em meios heterogêneos e anisotrópicos.

1. Percolação de água no solo
PRINCÍPIOS
ENG. JESELAY REIS
UEM/DEC
Utilizando como parâmetro o as instruções para implantação de linhas de transmissão e/ou distribuição de energia elétrica e telecomun

2. Água no Solo

3. Água no Solo

4. ÀGUA NAS ESTRUTURAS

5. ÀGUA NAS ESTRUTURAS

6. ÀGUA NAS ESTRUTURAS

7. ÀGUA NAS ESTRUTURAS

8. ÀGUA NAS ESTRUTURAS

9. Lei de Darcy
A
i
k
Q .
.

A
L
H
k
Q .
.


A
H
L
Q
k
.
.


Vazão
Gradiente Hidráulico
L
H
i


Coeficiente de permeabilidade

10. Determinação do coeficiente de permeabilidade
A
H
L
Q
k
.
.


Permeâmetro de carga constante

11. Determinação do coeficiente de permeabilidade
f
i
H
H
A
t
L
a
k log
.
.
3
,
2


Permeâmetro de carga variável

12. Determinação do coeficiente de permeabilidade
2
.
100 ef
D
k 
Permeâmetro de carga variável

13. Equação de Bernoulli
CA
PIEZÔMETRI
A
ALTIMÉTRIC
TOTAL H
H
H 

CINÉTICA
CA
PIEZÔMETRI
A
ALTIMÉTRIC
TOTAL H
H
H
H 


g
v
u
z
H
w
TOTAL
2
2




z
H a
Altimétric 
w
ca
Piezômetri
u
H


g
v
Hcinética
.
2
2


14. Equação de Bernoulli
    B
A
B
T
A
T H
H
H ,



        B
A
B
P
B
A
A
P
A
A H
H
H
H
H ,






15. Equação Geral de Fluxo em Meio Contínuo





















e
t
S
S
t
e
e
z
H
k
y
H
k
x
H
k
o
z
y
x .
1
1
2
2
2
2
2
2

16. Equação Geral de Fluxo em Meio Contínuo





















e
t
S
S
t
e
e
z
H
k
y
H
k
x
H
k
o
z
y
x .
1
1
2
2
2
2
2
2





















e
t
S
S
t
e
e
z
H
k
y
H
k
x
H
k
o
z
y
x .
1
1
2
2
2
2
2
2
Meio Saturado
Meio Saturado

17. Equação Geral de Fluxo em Meio Contínuo





















e
t
S
S
t
e
e
z
H
k
y
H
k
x
H
k
o
z
y
x .
1
1
2
2
2
2
2
2





















e
t
S
S
t
e
e
z
H
k
y
H
k
x
H
k
o
z
y
x .
1
1
2
2
2
2
2
2
Meio
estacionário Meio Saturado

18. Equação Fluxo em Meio Contínuo estacionário e
saturado
0
2
2
2
2
2
2









z
H
k
y
H
k
x
H
k z
y
x
0
2
2
2
2






z
H
k
x
H
k z
x
Meio bidimensional

19. Equação Fluxo em Meio Contínuo estacionário e
saturado bidimensional
0
2
2
2
2






z
H
k
x
H
k z
x
Homogêneo e Isotrópico
y
x k
k 
0
2
2
2
2






z
H
x
H
Laplace

20. Equação Fluxo em Meio Contínuo estacionário e
saturado bidimensional homogênio e isotrópico
0
.
.
2
2
2
2














 
Hi
Ho
Fi
Fo
dz
dx
z
H
x
H
Laplace
Solução por
integração
0
2
2
2
2






z
H
x
H

21. Equação Fluxo em Meio Contínuo estacionário e
saturado bidimensional homogênio e isotrópico
Famílias de curvas
0
2
2
2
2






z
H
x
H
Função de corrente
Função de potencial

22. Solução de Problemas de valor de contorno
Famílias de curvas
0
2
2
2
2






z
H
x
H
Função de
corrente
Função de
potencial
Linhas de fluxo
Linhas
equipotenciais

23. Solução de Problemas de valor de contorno
Linhas que delimitam o canal de fluxo
Linhas
equipotenciais
Linhas de fluxo
Linhas de mesmo potencial hidráulico

24. Tipos de Fluxo
Quando o fluxo possui todas as condições de contorno
Não confinado
Confinado
Quando o fluxo não possui todas as condições de contorno

25. Confinado
Linhas de Fluxo
Linhas equipotencial

26. Não confinado
Linhas de Fluxo
Linhas equipotenciais

27. Traçado da Linha
Freática

28. Traçado da Linha
Freática

29. Traçado da Linha
Freática

30. Traçado da Linha
Freática

31. Traçado da Linha
Freática

32. Solução de Problemas de valor de contorno
Numérica
Analitica
Por analogia
Gráfica Redes de fluxo

33. Redes de fluxo

34. Redes de fluxo

35. Redes de fluxo
q
q
h1
h2
h
k
q 
 .
2
1 h
h
h 



36. Redes de fluxo
q
q
h1
h2
h
k
q 
 .
2
1 h
h
h 



37. Redes de fluxo
q
q
h1
h2
h
k
q 
 .
2
1 h
h
h 



38. Redes de fluxo
q
q
h1
h2
h
k
q 
 .
A
i
k
q .
.
 b
l
h
k
q .
.


qp
n
H
h



Como
qp
n
H
k
q

 . .
.
.
qp
cf
n
n
H
k
Q 

b
l 

39. Exemplo

40. Exemplo

41. Exemplo
.
.
.
qp
cf
n
n
H
k
Q 
 forma
de
fator
n
n
qp
cf


42. Exemplo
.
.
.
qp
cf
n
n
H
k
Q 
 forma
de
fator
n
n
qp
cf


43. Exemplo
.
.
.
qp
cf
n
n
H
k
Q 
 forma
de
fator
n
n
qp
cf


44. Exemplo

45. Exemplo
.
.
.
qp
cf
n
n
H
k
Q 
 forma
de
fator
n
n
qp
cf


46. Exemplo
.
.
.
qp
cf
n
n
H
k
Q 
 forma
de
fator
n
n
qp
cf


47. Exemplo
.
.
.
qp
cf
n
n
H
k
Q 
 forma
de
fator
n
n
qp
cf


48. Gradiente Hidráulico
flow
10/19/2022
W
Pw
Fp
A
h
P w
w
w .
.


A
L
W sat .
.


A
u
Fp .

w
p
u
H


:
onde
w
p
H
u 
.
 A
H
F w
P
p .
.

0


 P
w F
W
P
H

w
h
L

49. Gradiente Hidráulico
flow
10/19/2022
W
Pw
Fp
A
h
P w
w
w .
.


A
L
W sat .
.


A
H
F w
P
p .
.

0


 P
w F
W
P
H

w
h
L
0
.
.
.
.
.
. 

 A
H
A
L
A
h w
P
sat
w
w 


0
.
.
. 

 w
P
sat
w
w H
L
h 


0
).
(
.
. 




 w
w
sat
w
w H
h
L
L
h 



50. Gradiente Hidráulico
flow
10/19/2022
W
Pw
Fp
H

w
h
L
0
).
(
.
. 




 w
w
sat
w
w H
h
L
L
h 


0
.
.
. 


 w
w
sat H
L
L 


0
.
)
.( 


 w
w
sat H
L 


)
.(
. w
sat
w L
H 

 


w
w
sat
L
H


 )
( 



51. Gradiente Hidráulico
10/19/2022
w
w
sat
L
H


 )
( 


flow
W
Pw
Fp
H

w
h
L
L
H
iatuante


w
w
sat
crítico
i


 )
( 

w
sub
crítico
i



crítico
atuante i
i 

52. Traçado da Rede de Fluxo
10/19/2022

53. Condições de entrada de fluxo
10/19/2022

54. Condições de saída de fluxo
10/19/2022

55. Traçado da Rede de Fluxo
10/19/2022

56. Traçado da Rede de Fluxo
10/19/2022

57. Traçado da Rede de Fluxo
10/19/2022

58. Traçado da Rede de Fluxo
10/19/2022

59. Traçado da Rede de Fluxo
10/19/2022

60. Traçado da Rede de Fluxo
10/19/2022

61. Fluxo em meio heterogêneo e anisotrópico
 Fluxo em meio homegêneo
 Propriedades iguais em
todos os pontos
 Fluxo em meio heterogêneo
 Propriedades diferentes
 Fluxo em meio isotrópico
 Mesma propriedades em
todas as direções
 Fluxo em meio anisotrópico
 Propriedades diferentes
em cada direção
www.usgs.gov

62. Fluxo em meio heterogêneo e anisotrópico
www.usgs.gov
Quando os coeficientes de permeabilidade são diferentes nas duas
direções (kx ≠ kz), o traçado da rede de fluxo requer que seja desenhada
previamente uma seção transformada.

63. Equação Fluxo em Meio Contínuo estacionário e
saturado bidimensional
0
2
2
2
2






z
H
k
x
H
k z
x
Homogêneo e Isotrópico
y
x k
k 
0
2
2
2
2






z
H
x
H
Laplace

64. Equação Fluxo em Meio Contínuo estacionário e
saturado bidimensional
0
2
2
2
2






z
H
k
x
H
k z
x
Homogêneo e Isotrópico
y
x k
k 
0
2
2
2
2






z
H
k
x
H
k z
x

65. Equação Fluxo em Meio Contínuo estacionário e
saturado bidimensional
0
2
2
2
2






z
H
k
x
H
k z
x
z
x k
k 
0
2
2
2
2






z
H
k
k
x
H
k
k
z
z
z
x
0
2
2
2
2






z
H
x
H
k
k
z
x
0
1
2
2
2
2













 z
H
x
H
k
k
x
z

66. Equação Fluxo em Meio Contínuo estacionário e
saturado bidimensional
0
1
2
2
2
2













 z
H
x
H
k
k
x
z
0
2
2
2
2






















z
H
k
k
x
H
x
z
 
0
2
2
2
2






z
H
X
H
T









x
z
T
k
k
x
X
Laplace

67. Fluxo em meio ANISOTRÓPICO

68. Fluxo em meio ANISOTRÓPICO

69. Fluxo em meio ANISOTRÓPICO

70. Fluxo em meio ANISOTRÓPICO

71. .
.
.
qp
cf
E
EQUIVALENT
n
n
H
k
Q 

z
x
E
EQUIVALENT k
k
k .

Fluxo em meio ANISOTRÓPICO

72. Camadas paralelas ao fluxo
Q  Qi
i1
3

 (biKi
h
x
)
i1
3

 
h2  h1
W
(biKi )
i1
3

biKi
i1
3
  bK
 



3
1
1
i
i
i
fluxo
paralela
camada K
b
b
K
3
K
2
K
1
K
W
b
Q
1
b
2
b
3
b
1
Q
2
Q
3
Q
Q  
h2  h1
W
bK
Fluxo em meio HETEROGÊNEO

73. Camadas perpendiculares ao fluxo


















3
1
i i
i
i
i
i
i
i
i
K
b
A
Q
A
K
Q
b
h
b
h
A
K
Q
b
K

bi
Ki






i1
3











 3
1
i i
i
fluxo
lar
perpendicu
camada
K
b
b
K
Q
3
K
2
K
1
K
A
b
1
b
2
b
3
b
1
h

2
h

3
h

Q
K
b
A
Q
h
b
h
A
K
Q







74. Fluxo em meio heterogêneo

75. Fluxo em meio heterogêneo

76. Fluxo em meio heterogêneo

77. Fluxo em meio heterogêneo

78. Fluxo em meio heterogêneo

79. Exercício 1.

80. Exercício 2.