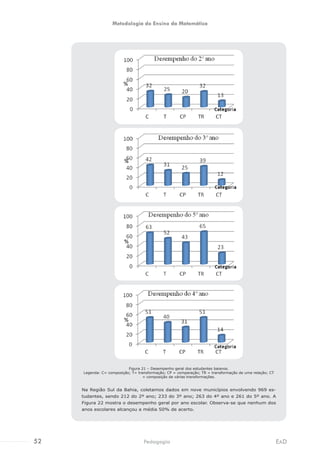
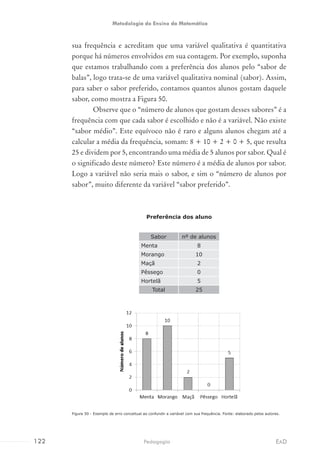
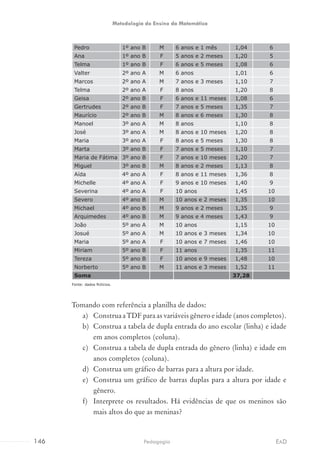
1. O documento apresenta um capítulo sobre a construção do conceito de número, discutindo como as crianças desenvolvem habilidades como classificação, seriação e contagem desde cedo.
2. São apresentadas atividades com imagens que estimulam essas habilidades, como classificar objetos em grupos, ordenar uma série, comparar quantidades e contar objetos.
3. O desenvolvimento dessas habilidades é fundamental para a aprendizagem do conceito de número nos anos iniciais do ensino fundamental.



![Ficha Catalográfica
1ª edição | Julho de 2012 | 476 exemplares
Copyright by EAD-UAB/UESC
Projeto Gráfico e Diagramação
Jamile Azevedo de Mattos Chagouri Ocké
João Luiz Cardeal Craveiro
Saul Edgardo Mendez Sanchez Filho
Capa
Saul Edgardo Mendez Sanchez Filho
Impressão e acabamento
JM Gráfica e Editora
Todos os direitos reservados à EAD-UAB/UESC
Obra desenvolvida para os cursos de Educação a
Distância da Universidade Estadual de Santa Cruz -
UESC (Ilhéus-BA)
Campus Soane Nazaré de Andrade - Rodovia Ilhéus-
Itabuna, Km 16 - CEP 45662-900 - Ilhéus-Bahia.
www.nead.uesc.br | uabuesc@uesc.br | (73) 3680.5458
Pedagogia | Módulo 5 | Volume 3 - Metodologia do Ensino da Matemática
Metodologia do ensino da matemática / Elaboração de
conteúdo: Aida Carvalho Vita ... [et al.]. – Ilhéus,
BA: Editus, 2012.
175 p. : il. (Pedagogia – módulo 5 – volume 3 – EAD)
ISBN: 978-85-7455-295-8
1. Matemática – Estudo e ensino. 2. Matemática –
Metodologia. I. Vita, Aida Carvalho. II. Série.
CDD 510.7
593](https://image.slidesharecdn.com/modulo-matematica-150616133747-lva1-app6892/85/Modulo-matematica-4-320.jpg)













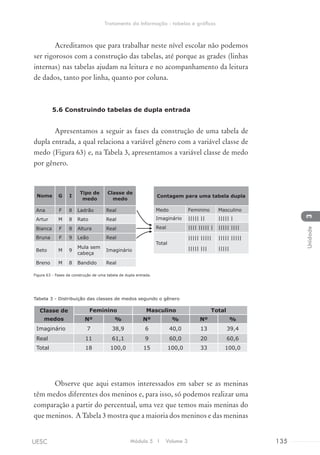
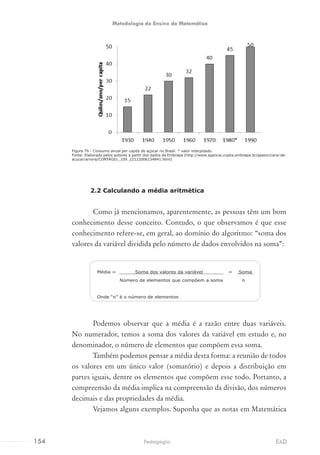
![c) Quantificadores: expressam relação de quantidade de objetos,
identificando onde há mais ou menos objetos, associam elementos
e os representam com seus indicadores. Por exemplo, na Figura
3, solicitar à criança que assinale em qual dos dois conjuntos há
menos borboletas.
Figura 3 - Exemplo de atividade com quantificadores com o software ITS.
Outra forma de quantificação faz referência à aplicação de
quantificadores básicos de uma coleção de objetos (todos, nenhum,
alguns, nada, pouco, [...]), como no exemplo da Figura 4.
Figura 4 - Exemplo de atividade de quantificação com o software ITS
18 EADPedagogia
Metodologia do Ensino da Matemática](https://image.slidesharecdn.com/modulo-matematica-150616133747-lva1-app6892/85/Modulo-matematica-18-320.jpg)




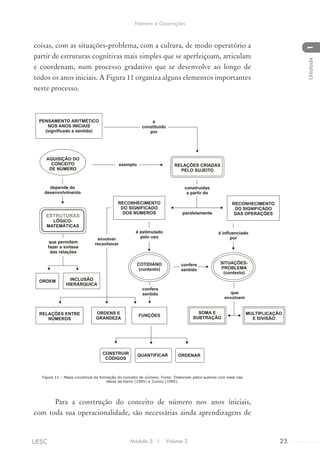
















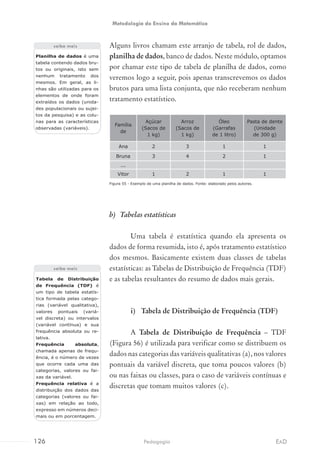
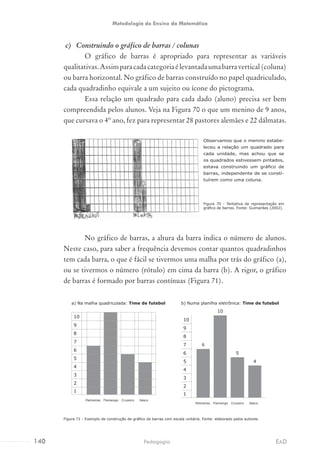
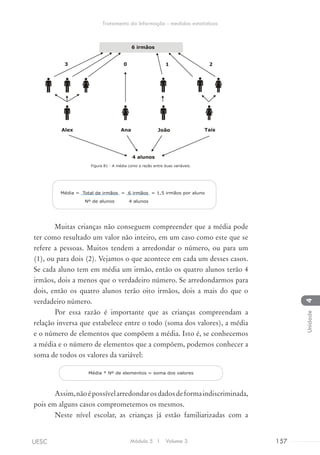
![Na multiplicação, podemos:
a) Decompor um dos fatores e usar a
propriedade distributiva. Por exemplo: 7 x 15
7 x 15 =
(7 x 10) + (7 x 5) =
70 + 35 = 105
b) Utilizar a propriedade distributiva da
multiplicação em relação a soma. Por
exemplo: 32 x 5
(30 + 2) x 5 =
30 x 5 + 2 x 5 =
150 + 10 = 160
Na divisão, podemos:
a) Fazer simplificações sucessivas. Por exemplo:
512 : 32
512 : 32 =
256 : 16 =
128 : 8 =
64 : 4 =
32 : 2 =
16
b) Decompor e utilizar a propriedade distributiva.
Por exemplo: 75 : 5
75 : 5 = (70 + 5) : 5 =
70 : 5 + 5 : 5 =
24 + 1 = 25
As habilidades para fazer estimativas e cálculo mental dão
autoconfiança aos alunos e os tornam mais autônomos, permitindo que
avaliem as situações e tomem decisões quanto à importância do cálculo
exato. Os PCN (BRASIL, 2000), em relação aos procedimentos sobre
números e operações no primeiro ciclo, enfatizam a necessidade da
[...] utilização da decomposição das escritas numéricas
para a realização do cálculo mental exato e aproxima-
do. Cálculos de adição e subtração por meio de estra-
tégias pessoais e algumas técnicas convencionais. Cál-
: 2
: 2
: 2
: 2
40 EADPedagogia
Metodologia do Ensino da Matemática](https://image.slidesharecdn.com/modulo-matematica-150616133747-lva1-app6892/85/Modulo-matematica-40-320.jpg)



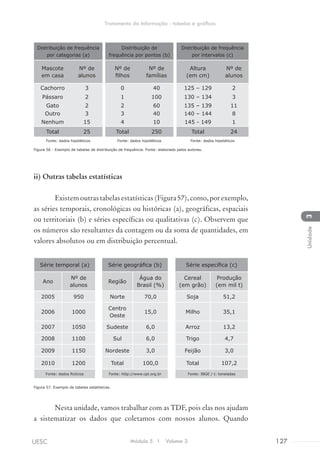
![d) Agora, na casa das dezenas, temos
12 bolinhas e podemos retirar 3;
e) Finalmente, das 6 centenas
retiramos 4 e obtemos 294.
6 O CAMPO CONCEITUAL ADITIVO
Geralmente, trabalhamos na escola com as operações de adição,
subtração, multiplicação e divisão sem fazer maiores relações com os
problemas matemáticos que envolvem tais operações. O pesquisador
francês Gérard Vergnaud estudou essas operações de modo a trabalhar os
conceitos envolvidos nos problemas matemáticos e relacionados com tais
operações.
Esse pesquisador desenvolveu a Teoria dos Campos Conceituais
(TCC) que é uma “teoria cognitivista que [...] tem uma forte herança
da teoria de Piaget e, também, alguns pontos da teoria de Vygotsky”
(SANTANA, 2010, p. 24).
Para Vergnaud (1982, 1996), o Campo Conceitual das Estruturas
Aditivas, ou de maneira mais simples, o Campo Aditivo é, ao mesmo tempo,
o conjunto das situações cujo tratamento implica uma ou várias adições ou
subtrações, e o conjunto dos conceitos e teoremas que permite analisar essas
situações como tarefas matemáticas. O Campo Conceitual das Estruturas
Multiplicativas ou o Campo Multiplicativo é definido no mesmo sentido do
aditivo sendo que as operações são as de multiplicação e divisão.
Antes de estudar sobre a classificação das situações-problema de aditivas, elabore seis situa-
ções-problema de adição e/ou subtração. Siga o estilo dos que geralmente você trabalha em
sua sala de aula. Essa atividade deverá ser postada.
A atividade tem por objetivo mapear as categorias que você utiliza na sua prática pedagógi-
ca. Ao final desta unidade, retome as situações-problema que você elaborou e verifique se
trabalha com todas as categorias.
sugestão de atividade
7 2 5
4 3 1
1
-
9 4
6
7 2 5
4 3 1
1
-
6
2 9 4
44 EADPedagogia
Metodologia do Ensino da Matemática](https://image.slidesharecdn.com/modulo-matematica-150616133747-lva1-app6892/85/Modulo-matematica-44-320.jpg)