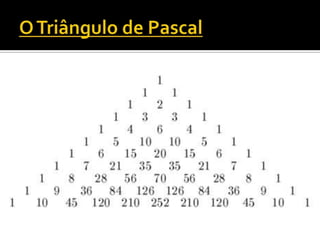
O documento explica o que é um binômio de Newton, que é uma expressão da forma (a + b)n, onde n é um número natural. Ele fornece exemplos de desenvolvimentos de binômios de Newton até o grau 4 e explica que o desenvolvimento resulta em um polinômio com n + 1 termos cuja soma dos coeficientes é igual a 2n.

2. Denomina-se Binômio de Newton , a todo binômio
da forma (a + b)n , sendo n um número natural .
Exemplo:
B = (3x - 2y)4, onde a = 3x, b = -2y e n = 4
Exemplos de desenvolvimento de binômios de Newton :
a) (a + b)2 = a2 + 2ab + b2
b) (a + b)3 = a3 + 3 a2b + 3ab2 + b3
c) (a + b)4 = a4 + 4 a3b + 6 a2b2 + 4ab3 + b4
d) (a + b)5 = a5 + 5 a4b + 10 a3b2 + 10 a2b3 + 5ab4 + b5

4. Usando a regra prática acima, o
desenvolvimento do binômio de Newton
(a + b)7 será:
(a + b)7 = a7 + 7 a6b + 21 a5b2 + 35 a4b3 + 35
a3b4 + 21 a2b5 + 7 ab6 + b7

5. Observações:
1) o desenvolvimento do binômio (a + b)n é um
polinômio.
2) o desenvolvimento de (a + b)n possui n + 1 termos
3) os coeficientes dos termos equidistantes dos
extremos , no desenvolvimento de (a + b)n são iguais
4) a soma dos coeficientes de (a + b)n é igual a 2n .

6. Fórmula do termo geral de um Binômio de
Newton
Um termo genérico Tp+1 do desenvolvimento
de (a+b)n , sendo p um número natural, é dado
por:
onde:

7. Exercicios
1 - Determine o 7º termo do binômio (2x + 1)9 ,
desenvolvido segundo as potências decrescentes
de x.
2 - Qual o termo médio do desenvolvimento de
(2x + 3y)8 ?
3 - Desenvolvendo o binômio (2x - 3y)3n , obtemos
um polinômio de 16 termos . Qual o valor de n?
4 - Determine o termo independente de x no
desenvolvimento de (x + 1/x )6 .

8. Fim.