DM
Carregado porDiego Machado
1,351 visualizações

Mec�nica dos fluidos

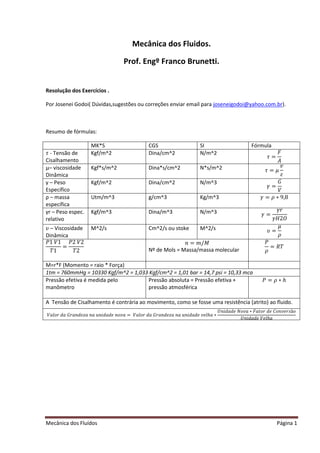
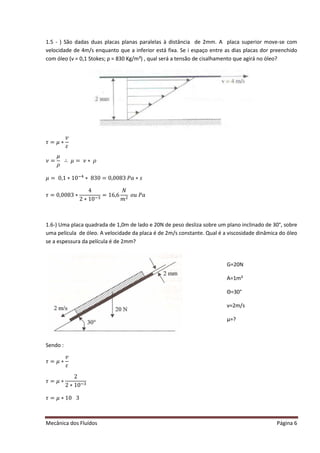
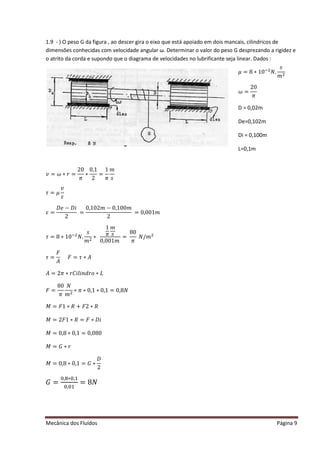
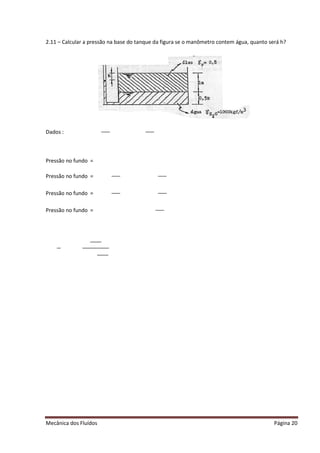
O documento fornece resumos de fórmulas e conceitos fundamentais da mecânica dos fluidos, incluindo tensão de cisalhamento, viscosidade dinâmica, peso específico, massa específica, viscosidade cinemática e equações de estado. Exemplos numéricos são fornecidos para ilustrar o cálculo destas grandezas nos sistemas MK*S, CGS e SI.

Incorporar apresentação

Baixado 10 vezes
Mecânica dos Fluídos Página 1 Mecânica dos Fluidos. Prof. Engº Franco Brunetti. Resolução dos Exercícios . Por Josenei Godoi( Dúvidas,sugestões ou correções enviar email para joseneigodoi@yahoo.com.br). Resumo de fórmulas: MK*S CGS SI Fórmula ߬- Tensão de Cisalhamento Kgf/m^2 Dina/cm^2 N/m^2 ߬= ‫ܨ‬ ‫ܣ‬ μ– viscosidade Dinâmica Kgf*s/m^2 Dina*s/cm^2 N*s/m^2 ߬= ߤ ‫ݒ‬ ߝ γ – Peso Específico Kgf/m^2 Dina/cm^2 N/m^3 ߛ = ‫ܩ‬ ܸ ρ – massa específica Utm/m^3 g/cm^3 Kg/m^3 ߛ = ߩ∗ 9,8 γr – Peso espec. relativo Kgf/m^3 Dina/m^3 N/m^3 ߛ = ߛ‫ݎ‬ ߛ‫ܱ2ܪ‬ ߭– Viscosidade Dinâmica M^2/s Cm^2/s ou stoke M^2/s ߭= ߤ ߩ ܲ1 ܸ1 ܶ1 = ܲ2 ܸ2 ܶ2 ݊ = ݉ /‫ܯ‬ Nº de Mols = Massa/massa molecular ܲ ߩ = ܴܶ M=r*F (Momento = raio * Força) 1tm = 760mmHg = 10330 Kgf/m^2 = 1,033 Kgf/cm^2 = 1,01 bar = 14,7 psi = 10,33 mca Pressão efetiva é medida pelo manômetro Pressão absoluta = Pressão efetiva + pressão atmosférica ܲ = ߩ∗ ℎ A Tensão de Cisalhamento é contrária ao movimento, como se fosse uma resistência (atrito) ao fluido. ܸ݈ܽ‫ܽ݀ݎ݋‬ ‫ܽݖ݁݀݊ܽݎܩ‬ ݊ܽ‫݅݊ݑ‬݀ܽ݀݁݊‫ܽݒ݋‬ = ܸ݈ܽ‫ܽ݀ݎ݋‬ ‫ܽݖ݁݀݊ܽݎܩ‬ ݊ܽ‫݅݊ݑ‬݀ܽ݀݁‫݈݁ݒ‬ℎܽ∗ ܷ݊݅݀ܽ݀݁ܰ‫ܽݒ݋‬∗ ‫ݐܽܨ‬‫ݏݎ݁ݒ݊݋ܥ݁݀ݎ݋‬ã‫݋‬ ܷܸ݈݊݅݀ܽ݀݁݁ℎܽ
Mecânica dos Fluídos Página 2 Capitulo 1 Fluidos 1.1 - ) A Massa específica de um fluído é 1200kg/m³. Determinar o seu peso específico e o peso específico relativo (g=9,8m/s²). Sendo: ρ= 1200 kg/m³ ߛ= ? g=9,8 m/s² ߛr = ? ߛ ൌ ߩ‫݃כ‬ ߛ ൌ ͳʹ ͲͲ‰Ȁ Ϳ‫ͻכ‬ǡͺ Ȁ•; ߛ ൌ ͳͳ͹͸ͲܰȀ݉ Ϳ ߛ‫ݎ‬ൌ ߛ ߛ‫ܪ‬ଶܱ Para g=10 m/s² ߛ ൌ ͳʹ ͲͲͲܰȀ݉ Ϳ sendo em SI ߛ‫ܪ‬ଶܱ ൌ ͳͲͲͲͲܰȀ݉ Ϳ ߛ‫ݎ‬ൌ ͳʹ ͲͲͲܰȀ݉ Ϳ ͳͲͲͲͲܰȀ݉ Ϳ ߛ‫ݎ‬ൌ ͳǡʹ 1.2 - ) A viscosidade cinemática de um óleo é de 0,028 m²/s e o seu peso específico relativo é de 0,85. Determinar a viscosidade cinemática nos sistemas MK*S, CGS, e SI (g=10 m/s² ) . γ=0,028 m²/s γr=0,85 μ=? ߛ ൌ ߛ‫ܪߛכݎ‬ଶܱ ߛ ൌ Ͳǡͺͷ‫כ‬ͳͲͲͲ‰ˆȀ Ϳ ߛ ൌ ͺͷͲ‰ˆȀ Ϳ ߩ ൌ ߛ ݃ ߩ ൌ 850 10 ߩ ൌ ͺͷ‫ݐݑ‬݉ Ȁ݉ Ϳ ߤ଴ ൌ ߛ଴ ‫ߩכ‬଴
Mecânica dos Fluídos Página 3 ߤ଴ ൌ ͲǡͲʹ ͺ݉ ;Ȁ‫ݏ‬‫כ‬ͺͷ‫ݐݑ‬݉ Ȁ݉ Ϳ ߤ଴ ൌ ʹ ǡ͵ ͺ݂݇݃Ǥ ‫ݏ‬ ݉ ଷ Para SI: ߛ ൌ ߛ‫ܪߛכݎ‬ଶܱ ߛ ൌ Ͳǡͺͷ‫כ‬ͳͲͲͲͲȀ Ϳ ߛ ൌ ͺͷͲͲȀ Ϳ ߩ ൌ ߛ ݃ ߩ ൌ 8500 10 ߩ ൌ ͺͷͲ‫݃ܭ‬Ȁ݉ Ϳ ߤ଴ ൌ ߛ଴ ‫ߩכ‬଴ ߤ଴ ൌ ͲǡͲʹ ͺ݉ ;Ȁ‫ݏ‬‫כ‬ͺͷͲ‫݃ܭ‬Ȁ݉ Ϳ ߤ଴ ൌ ʹ ͵ ǡͺܰǤ‫ݏ‬Ȁ݉ Ϳ ߛ ൌ ͲǡͲʹ ͺ mଶ s = (0,028 ∗ (10)ଶ)ଶ cm² s = 280 cm² s ou poise Como ͳܰ ൌ ͳͲହ ݀‫݊ݕ‬ ‫׷‬ ߛ ൌ ͺͷͲͲ‫Ͳͳכ‬ହ ݀‫݊ݕ‬ (10ଶ)ଷܿ݉ Ϳ ߛ ൌ ͺͷͲ ݀‫݊ݕ‬ ܿ݉ Ϳ ߩ ൌ 850 1000 = 0,85 ݃ ܿ݉ ଷ ߤ ൌ Ͳǡͺͷ‫ʹכ‬ ͺͲ ߤ ൌ ʹ ͵ ͺ ݀݅݊ܽǤ‫ݏ‬ ܿ݉ ଶ
Mecânica dos Fluídos Página 4 Ou transformando : Lembrando que : ܸ݈ܽ‫ݎ݋‬݀ܽ‫ܽݖ݁݀݊ܽݎܩ‬݊ܽ‫݅݊ݑ‬݀ܽ݀݁݊‫ܽݒ݋‬ ൌ ܸ݈ܽ‫ݎ݋‬݀ܽ‫ܽݖ݁݀݊ܽݎܩ‬݊ܽ‫݅݊ݑ‬݀ܽ݀݁‫݈݁ݒ‬݄ܽ‫כ‬ ܷ݊݅݀ܽ݀݁ܰ‫ܽݒ݋‬‫ݐܽܨכ‬‫ݎ݋‬݀݁‫ ݏݎ݁ݒ݊݋ܥ‬ ‫݋‬ ܷܸ݈݄݊݅݀ܽ݀݁݁ܽ Para SI: ߤ ൌ ʹ ǡ͵ ͺ ‫݂݃ܭ‬Ǥ‫ݏ‬ ݉ ; = 2,38 ‫݂݃ܭ‬൬ ܰ ‫ͻכ‬ǡͺ ‫݂݃ܭ‬ ൰ ݉ ; = 23,3 ܰǤ‫ݏ‬ ݉ ; Para CGS: ߤ ൌ ʹ ǡ͵ ͵ ܰǤ‫ݏ‬ ݉ ; = 2,38 ܰ ൬ ‫݅ܦ‬݊ܽ‫Ͳͳכ‬ହ ܰ ൰ ݉ ² ൬ ܿ݉ ; ‫Ͳͳכ‬ସ ݉ ² ൰ = 233 ‫݅ܦ‬݊ܽ‫ݏ‬ ܿ݉ ; ‫ݑ݋‬‫݅݋݌‬‫݁ݏ‬ 1.3 - ) A viscosidade dinâmica de um óleo é de 5 ∗ 10ିସ ௞௚௙Ǥ௦ ௠ మ e o peso específico relativo é de 0,82. Determinar a viscosidade cinemática nos sistemas MK*S SI e CGS. Considerar : g=10 m/s² e ߛ‫ܪ‬ଶܱ ൌ ͳͲͲͲ‫݂݃ܭ‬Ȁ݉ Ϳ ߛ ൌ ͷ‫Ͳͳכ‬ିଽ Kgf. s mଶ ߛ‫ݎ‬ൌ Ͳǡͺʹ ߛ ൌ ߛ‫ܪߛכݎ‬ଶܱ ߛ ൌ Ͳǡͺʹ ‫כ‬ͳͲͲͲ‰ˆȀ Ϳ ߛ ൌ ͺʹ Ͳ‰ˆȀ Ϳ ߩ ൌ ߛ ݃ ߩ ൌ 820 10 ߩ ൌ ͺʹ ‫݂݃ܭ‬Ǥ‫ݏ‬ଶ ݉ ସ ‫ݑ݋‬ ‫ݐݑ‬݉ ݉ ଷ ߭ൌ ߤ ߩ = 5 ∗ 10ିସ 82 = 6,1 ∗ 10ି଺ mଶ s MK ∗ S e SI ∴ ߭ൌ ͸ǡͳ‫Ͳͳכ‬ି଺ ∗ 10ସ = 6,1 ∗ 10ିଶ ܿ݉ ଶ ‫ݏ‬ ‫ݑ݋‬ܵ‫ݐ‬Ǥ
Mecânica dos Fluídos Página 5 1.4 - ) O peso de 3dm³ de uma substância é 23,5 N. A viscosidade Cinemáica é de 10ିହ௠ మ ௦ . Se g=10 m/s² qual será a viscosidade dinâmica nos sistemas CGS, MK*S e em N. min/km² e SI? ‫ݒ‬ ൌ ͵ ݀݉ ଷ = 3 ∗ 10ିଷ ݉ ଷ Sendo : ߛ ൌ ீ ௏ ‫ݐ‬݁݉ ‫ݏ݋‬‫݁ݑݍ‬‫׷‬ ߛ ൌ ‫ܩ‬ ܸ = ʹ ͵ ǡͷܰ 3 ∗ 10ିଷ݉ ଷ = 7833 ܰ ݉ ଷ e : ߩ ൌ ߛ ݃ ߩ ൌ 7833 10 = 783,3 ‫݃ܭ‬ ݉ ଷ ߤ ൌ ߭‫ߩכ‬ ߤ ൌ ͳͲିହ ݉ ଶ ‫ݏ‬ ∗ 783,3 ‫݃ܭ‬ ݉ ଷ = 7,83 ∗ 10ିଷ ܰ ‫ݏכ‬ ݉ ଶ Lembrando que : ‫݃ܭ‬ ൌ ே ೘ ೞమ Convertendo : ܸ݈ܽ‫ݎ݋‬݀ܽ‫ܽݖ݁݀݊ܽݎܩ‬݊ܽ‫݅݊ݑ‬݀ܽ݀݁݊‫ܽݒ݋‬ ൌ ܸ݈ܽ‫ݎ݋‬݀ܽ‫ܽݖ݁݀݊ܽݎܩ‬݊ܽ‫݅݊ݑ‬݀ܽ݀݁‫݈݁ݒ‬݄ܽ‫כ‬ ܷ݊݅݀ܽ݀݁ܰ‫ܽݒ݋‬‫ݐܽܨכ‬‫ݎ݋‬݀݁‫ ݏݎ݁ݒ݊݋ܥ‬ ‫݋‬ ܷܸ݈݄݊݅݀ܽ݀݁݁ܽ Para SI: ߤ ൌ ͹ǡͺ͵ ‫Ͳͳכ‬ିଷ ܰǤ‫ݏ‬ ݉ ; = 7,83 ∗ 10ିଷ ܰ ൬ ‫݂݃ܭ‬ ܰ ∗ 9,8 ൰‫ݏכ‬ ݉ ; = 8 ∗ 10ିସ ݂݇݃‫ݏכ‬ ݉ ; Para CGS: ߤ ൌ ͹ǡͺ͵ ‫Ͳͳכ‬ିଷ ܰǤ‫ݏ‬ ݉ ; = 7,83 ∗ 10ିଷ ܰ ൬ ‫݅ܦ‬݊ܽ‫Ͳͳכ‬ହ ܰ ൰ ݉ ² ൬ ܿ݉ ; ‫Ͳͳכ‬ସ ݉ ² ൰ = 7,83 ∗ 10ିଶ ‫݅ܦ‬݊ܽ‫ݏ‬ ܿ݉ ; ‫ݑ݋‬‫݅݋݌‬‫݁ݏ‬ Para ே௠ ௜௡ ௄௠ ; : ߤ ൌ ͹ǡͺ͵ ‫Ͳͳכ‬ିଷ ܰǤ‫ݏ‬ ݉ ; = 7,83 ∗ 10ିଷ ܰ‫ݏ‬ቀ ݉ ݅݊ ‫כݏ‬͸Ͳ ቁ‫ݏכ‬ ݉ ; ൬ ‫݉ܭ‬ ଶ ݉ ଶ ∗ 10଺൰ = 130,5 ܰ݉ ݅݊ ‫݉ܭ‬ ;
Mecânica dos Fluídos Página 6 1.5 - ) São dadas duas placas planas paralelas à distância de 2mm. A placa superior move-se com velocidade de 4m/s enquanto que a inferior está fixa. Se i espaço entre as dias placas dor preenchido com óleo (ν = 0,1 Stokes; ρ = 830 Kg/m³) , qual será a tensão de cisalhamento que agirá no óleo? ߬ൌ ߤ‫כ‬ ‫ݒ‬ ߝ ߥ ൌ ߤ ߩ ‫׵‬ ߤ ൌ ߥ‫כ‬ߩ ߤ ൌ Ͳǡͳ‫Ͳͳכ‬ିସ ‫כ‬ͺ͵ Ͳ ൌ ͲǡͲͲͺ͵ ܲܽ‫ݏכ‬ ߬ൌ ͲǡͲͲͺ͵ ‫כ‬ 4 2 ∗ 10ିଷ = 16,6 ܰ ݉ ଶ ‫ݑ݋‬ܲܽ 1.6-) Uma placa quadrada de 1,0m de lado e 20N de peso desliza sobre um plano inclinado de 30°, sobre uma película de óleo. A velocidade da placa é de 2m/s constante. Qual é a viscosidade dinâmica do óleo se a espessura da película é de 2mm? Sendo : ߬ൌ ߤ‫כ‬ ‫ݒ‬ ߝ ߬ൌ ߤ‫כ‬ 2 2 ∗ 10ିଷ ߬ൌ ߤ‫Ͳͳכ‬ ͵ G=20N A=1m² Θ=30° v=2m/s μ=?
Mecânica dos Fluídos Página 7 Também temos : ߬ൌ ‫ܨ‬ ‫ܣ‬ = 20 cos(60°) 1 = ͳͲܰ ݉ ଶ ∴ ͳͲ ൌ ߤ‫Ͳͳכ‬ଷ ߤ ൌ ͳͲିଶ ܰǤܵ ݉ ଶ 1.7 - ) Um eixo cilíndrico vertical de diâmetro 10cm gira no interior de um mancal de diâmetro 10,005 cm. A folga entre eixo e mancal é preenchida com óleo de viscosidade dinâmica ߤ ൌ ͳͲିଶ ேǤ௦ ௠ మ . Se o mancal tem comprimento de 25cm e o eixo gira com uma rotação de 1500 rpm, qual o momento resistente à rotação?
Mecânica dos Fluídos Página 8 1..8 - ) Um pistão cai dentro de um cilindro com velocidade constante de 3,2 m/s. Entre o pistão e o cilindro existe uma película de óleo de viscosidade cinemática ߥൌ ͳͲିଷ ௠ మ ௦ ݁ߛ ൌ ͺͺͲͲ ே ௠ య . Sendo o diâmetro do pistão 10cm, seu comprimento 5cm e o diâmetro do cilindro 10,2 cm , determinar o peso do pistão. (g=10m/s²). ߬ൌ ߤ‫כ‬ ‫ݒ‬ ߝ ߩ ൌ ߛ ݃ ߩ ൌ 8800 10 = 880 ‫݃ܭ‬ ݉ ଷ ߥ ൌ ߤ ߩ ‫׵‬ ߤ ൌ ߥ‫כ‬ߩ ߤ ൌ ͳͲିଷ ∗ 880 = 0,88 ܰ ݉ ଶ ߬ൌ Ͳǡͺͺ‫כ‬ 10ିଷ 0,1 ∗ 10ିଶ = 2816 ܰ ݉ ଶ ‫ܣ‬ ൌ ߨ ‫Ͳͳכ‬‫Ͳͳכ‬ିଶ ∗ 5 ∗ 10ିଶ ൌ ͷͲߨ ‫Ͳͳכ‬ିସ ߬ൌ ‫ܩ‬ ‫ܣ‬ = 2816 = ‫ܩ‬ ͷͲߨ ‫Ͳͳכ‬ିସ G = ͷͲߨ ‫Ͳͳכ‬ିସ ‫כ‬ʹ ͺͳ͸ ൌ ͶͶǡʹ ͵ ͵ ͸ܰ؆ ͶͶǡʹ ܰ ߥ ൌ ͳͲିଷ ݉ ଶ ‫ݏ‬ ߛ ൌ ͺͺͲͲ ܰ ݉ ଷ V=3,2m/s Di = 10cm L = 5cm De = 10,2cm Pp = ?
Mecânica dos Fluídos Página 9 1.9 - ) O peso G da figura , ao descer gira o eixo que está apoiado em dois mancais, cilindricos de dimensões conhecidas com velocidade angular ω. Determinar o valor do peso G desprezando a rigidez e o atrito da corda e supondo que o diagrama de velocidades no lubrificante seja linear. Dados : ‫ݒ‬ ൌ ߱ ‫ݎכ‬ൌ 20 ߨ ∗ 0,1 2 = 1 ߨ ݉ ‫ݏ‬ ߬ൌ ߤ ‫ݒ‬ ߝ ߝൌ ‫݁ܦ‬െ ‫݅ܦ‬ 2 = ͲǡͳͲʹ ݉ െ ͲǡͳͲͲ݉ 2 ൌ ͲǡͲͲͳ݉ ߬ൌ ͺ‫Ͳͳכ‬ିଶ ܰǤ ‫ݏ‬ ݉ ଶ ∗ 1 ߨ ݉ ‫ݏ‬ ͲǡͲͲͳ݉ = 80 ߨ ܰȀ݉ ଶ ߬ൌ ‫ܨ‬ ‫ܣ‬ ‫ܨ‬ ൌ ߬‫ܣכ‬ ‫ܣ‬ ൌ ʹ ߨ ‫݅ܥݎכ‬݈݅݊݀‫݋ݎ‬‫ܮכ‬ ‫ܨ‬ ൌ 80 ߨ ܰ ݉ ଶ ‫ߨכ‬ ‫Ͳכ‬ǡͳ‫Ͳכ‬ǡͳ ൌ Ͳǡͺܰ ‫ܯ‬ ൌ ‫ͳܨ‬‫ܴכ‬ ൅ ‫ʹܨ‬ ‫ܴכ‬ ‫ܯ‬ ൌ ʹ ‫ͳܨ‬‫ܴכ‬ ൌ ‫ܨ‬ ‫݅ܦכ‬ ‫ܯ‬ ൌ Ͳǡͺ‫Ͳכ‬ǡͳ ൌ ͲǡͲͺͲ ‫ܯ‬ ൌ ‫ܩ‬ ‫ݎכ‬ ‫ܯ‬ ൌ Ͳǡͺ‫Ͳכ‬ǡͳ ൌ ‫ܩ‬ ‫כ‬ ‫ܦ‬ 2 ‫ܩ‬ ൌ ଴ǡ଼‫כ‬଴ǡଵ ଴ǡ଴ଵ ൌ ͺܰ ߤ = 8 ∗ 10ିଶ ܰ. ‫ݏ‬ ݉ ଶ ߱ ൌ 20 ߨ D = 0,02m De=0,102m Di = 0,100m L=0,1m
Mecânica dos Fluídos Página 10 1.11 - ) Um viscosímetro de cilindros coaxiais é mostrado na figura. O cilindro externo está ligado a um eixo que transmite uma certa velocidade angular ω por meio de um motor. O Cilindro interno está suspenso por meio de um fio calibrado à torção. Quando o cilindro externo gira, devido as tensões de cisalhamento transmitidas pelo fluido, tende a girar o interno de forma a torcer o fio até que o esforço de torção no mesmo equilibre a ação das tensões de cisalhamento na periferia do cilindro interno. Sobre o fio pode estar montado um ponteiro que indicará sobre um mostrador previamente calibrado, o momento torçor aplicado. Dados: Mt= momento torçor, D1, De, ω, h, determinar a expressão que permite calcular a viscosidade do fluido à ser testado. Efetuar o problema em duas etapas: a) Desprezando o efeito do fluido; b) Levando em conta o efeito do mesmo. Onde ho = altura de líquido que causaria o mesmo efeito na base. Sugestão : considerar duas experiências com h1 e h2 diferentes, obter Mt1 e Mt2 e calcular o valor de ho. Solução : Pela lei de Newton do cisalhamento temos : ߬ൌ ߤ ݀‫ݒ‬ ݀‫ݕ‬ ൌ ߤ ‫݋ݒ‬ ߝ ‫ߤܨ‬ ‫ܣ‬ ൌ ߤ ‫݋ݒ‬ ߝ ‫ݒ‬ ൌ ߱‫ݎ‬ ‫ߤܨ‬ ൌ ‫݋ݒ‬‫ߤכ‬‫ܣכ‬ ߝ ‫ݒ‬ ൌ ߱݀݅ 2 ߝൌ ݀݁െ ݀݅ 2 ‫ܣ‬ ൌ ߨ ‫݄כ݅݀כ‬ Mt = Momento torçor ⇒ Mt – Marame = 0 ⇒ Mt = Marame
Mecânica dos Fluídos Página 11 Mt = Fμ * d ‫ܯ‬ ‫ݐ‬ൌ ‫݋ݒ‬‫ߤכ‬‫ܣכ‬ ߝ ‫ܯ‬ ‫ݐ‬ൌ ߤ‫߱כ‬ ‫כ݅݀כ‬ߨ ‫݄כ݅݀כ‬‫݅݀כ‬ 2 ∗ 2 ݀݁െ ݀݅ 2 ‫ܯ‬ ‫ݐ‬ൌ ߤ‫߱כ‬ ‫݅݀כ‬ଷ ‫כ‬ߨ ‫݄כ‬ ʹ ሺ݀݁െ ݀݅ሻ A - ) ࣆ ൌ ૛࢓ ࢚ሺࢊࢋିࢊ࢏ሻ ࣓‫࢏ࢊכࢎכ࣊כ‬૜ 1.12 - ) São dados dois planos paralelos à distância de 0,5 cm. O espaço entre os dois é preenchido com um fluído de ߤ ൌ ͳͲିହ ௄௚௙‫כ‬௦ ௠ మ . Qual será a força necessária para arrastar uma chapa de espessura 0,3 colocada a igual distância dos dois, de área ͳͲͲܿ݉ ଶ à velocidade de 0,15 ௠ ௦మ. ‫ܣ‬ ൌ ͳͲͲ‫Ͳͳכ‬ିସ ݉ ଶ = 10ିଷ ݉ ଶ ‫ܨ‬ൌ ‫ܣ‬ ‫ߤכ‬‫݋ݒכ‬ ‫ܧ‬ ‫ܨ‬ൌ 10ିଷ௠ మ ∗ 10ିହ ‫݂݃ܭ‬‫ݏכ‬ ݉ ଶ ∗ 0,15 ݉ ‫ݏ‬ 1 ∗ 10ିଷ݉ = 1,5 ∗ 10ି଺ ‫݂݃ܭ‬ ‫ܨ‬ ൌ ʹ ‫כ‬ͳǡͷ‫Ͳͳכ‬ି଺ ‫݂݃ܭ‬ ‫ܨ‬ ൌ ͵ ‫כ‬ͳͲିହ ‫݂݃ܭ‬
Mecânica dos Fluídos Página 12 1.13 - ) Assumindo o Diagrama de velocidades indicado na figura, no qual a parábola tem seu vértice a 10 cm do fundo, calcular o gradiente de velocidade e a tensão de cisalhamento para y=0; 5; 10cm. Adotar μ = 400 centipoises. ‫ݒ‬ ൌ ܽ‫ݕ‬ଶ ൅ ܾ‫ݕ‬൅ ܿ 1. ‫ܽݎܽ݌‬‫ݕ‬ ൌ Ͳǡͳ݉ ‫ݒ‬ ൌ ʹ ǡͷ ௠ ௦ ‫ݐݎ݋݌‬ܽ݊‫ݐ‬‫݋‬ ‫׷‬ʹ ǡͷ ൌ ܽ‫Ͳכ‬ǡͳଶ ൅ ܾ‫Ͳכ‬ǡͳ(1) 2. ‫ܽݎܽ݌‬‫ݕ‬ ൌ Ͳ‫ݒ‬ ൌ Ͳ‫ݐݎ݋݌‬ܽ݊‫ݐ‬‫݋‬ ‫׷‬ܿൌ Ͳ 3. ‫ܽݎܽ݌‬‫ݕ‬ ൌ Ͳǡͳ݉ ௗ௩ ௗ௬ ൌ Ͳ‫ݐݎ݋݌‬ܽ݊‫ݐ‬‫݋‬ ‫׷‬Ͳ ൌ ʹ ‫ܽכ‬‫Ͳכ‬ǡͳ൅ ܾൌ െͲǡʹ ܽ(2) ‫݁ܦ‬(2)݁݉ (1)ǣʹ ǡͷ ൌ ܽ‫Ͳכ‬ǡͳଶ െ Ͳǡͳ‫Ͳכ‬ǡʹ ‫ܽכ‬‫ݐݎ݋݌‬ܽ݊‫ݐ‬‫݋‬ܽൌ െʹ ͷͲ 1 ‫ܯ‬ ܵ ܾ ൌ ͷͲ ଵ ௦ ‫ݒ‬ൌ െʹ ͷͲ‫ݕ‬ଶ ൅ ͷͲ‫ݕ‬݁ ௗ௩ ௗ௬ ൌ െͷͲͲ‫ݕ‬൅ ͷͲ 1. ܲܽ‫ܽݎ‬‫ݕ‬ൌ Ͳ ௗ௩ ௗ௬ = 50 ଵ ௦ ‫ݐݎ݋݌‬ܽ݊‫ݐ‬‫݋‬ܶ ൌ ͶͲͲ‫כ‬ͳͲିଶ ∗ 50 = 200 ௗ௜௡௔ ௖௠ మ 2. ܲܽ‫ܽݎ‬‫ݕ‬ൌ ͲǡͲͷ ௗ௩ ௗ௬ = −500 ∗ 0,05 + 50 = 25 ଵ ௦ ‫ݐݎ݋݌‬ܽ݊‫ݐ‬‫݋‬ܶ ൌ ͶͲͲ‫כ‬ͳͲିଶ ∗ 25 = 100 ௗ௜௡௔ ௖௠ మ 3. ܲܽ‫ܽݎ‬‫ݕ‬ൌ Ͳǡͳ ௗ௩ ௗ௬ ൌ െͷͲͲ‫Ͳכ‬ǡͲͷ൅ ͷͲ ൌ Ͳ‫ݐݎ݋݌‬ܽ݊‫ݐ‬‫݋‬ܶ ൌ ͶͲͲ‫כ‬ͳͲିଶ ∗ 0 = 0 ௗ௜௡௔ ௖௠ మ 1.17 ) Um balão sonda de formato esférico foi projetado para ter um diâmetro de 10m a uma altitude de 45000m. Se a pressão e temperatura nesta altitude são respectivamente 2000Kgf/m^2 (abs) e -60ºC, determinar o volume de hidrogênio a 10000Kgf/m^2 (abs) e 20ºC necessário para encher o balão na terra. ܲͳ ൌ ʹ ͲͲͲ ௄௚௙ ௠ మ (ܾܽ‫)ݏ‬ ܲʹ ൌ ͳͲͲͲͲ ௄௚௙ ௠ మ (ܾܽ‫)ݏ‬ ܶͳ ൌ െ͸Ͳ͑ ‫ܥ‬ ൌ ʹ ͳ͵ ‫ܭ‬ ܶʹ ൌ െ͸Ͳ͑ ‫ܥ‬ ൌ ʹ ͻ͵ ‫ܭ‬ ܸܿൌ 4 3 ‫ߨכ‬ ‫ݎכ‬ଷ = 4 3 ‫ߨכ‬ ‫כ‬ͷଷ ܸܿൌ ͷʹ ͵ ǡͷͲ݉ ଷ ܲͳܸͳ ܶͳ = ܲʹ ܸʹ ܶʹ 2000 ‫݂݃ܭ‬ ݉ ଶ (ܾܽ‫)ݏ‬ͷʹ ͵ ǡͷͲ݉ ଷ ʹ ͳ͵ ‫ܭ‬ = 10000 ‫݂݃ܭ‬ ݉ ଶ (ܾܽ‫)ݏ‬ܸʹ ʹ ͻ͵ ‫ܭ‬ Ͷͻͳ͸ǡ͵ Ͷ‫כ‬ʹ ͻ͵ ‫ܭ‬ ൌ ͳͲͲͲͲ‫ʹܸכ‬ ܸʹ ൌ Ͷͻͳ͸ǡ͵ Ͷ‫כ‬ʹ ͻ͵ ‫ܭ‬ 10000 ܸʹ ൌ ͳͶͶǡͲͷ݉ ଷ
Mecânica dos Fluídos Página 13 1.18 - ) Um gás natural tem peso específico relativo 0,6 em relação ao ar a 10000Kgf/m² (abs) e 15°C. Qual o peso deste gás nas mesmas condições de pressão e temperatura? Qual a constante R deste gás? ቀܴ௔௥ = 287 ௠ మ ௦మ௄ Ǣ݃ ൌ ͻǡͺ ௠ ௦మቁ ߛ‫ݎ‬ൌ Ͳǡ͸ ൌ ߛ‫ݏ‬ ߛܽ‫ݎ‬ = ߛ‫ݏ‬݃ ߩܽ‫ݎ‬݃ ‫ݎܣ‬൜ ܲͳ ൌ ͳͲͲͲͲ‫݂݃ܭ‬Ȁ݉ ଶ(ܾܽ‫)ݏ‬ ܶͳ ൌ ͳͷι‫ܥ‬ ൅ ʹ ͹͵ ൌ ʹ ͺͺι‫ܭ‬ ߩܽ‫ݎ‬ൌ ܲ ܴܶ = 10000 287 = 0,21 ‫ݐݑ‬݉ ݉ ଷ ߛܽ‫ݎ‬ൌ ߩܽ‫݃כݎ‬ൌ Ͳǡʹ ͳ ‫ݐݑ‬݉ ݉ ଷ ∗ 9,8 ݉ ‫ݏ‬ଶ = 1,1858 ‫݂݃ܭ‬ ݉ ଷ ߛ݃ ൌ Ͳǡ͸‫כ‬ߛܽ‫ݎ‬ൌ Ͳǡ͹ͳͳ ‫݂݃ܭ‬ ݉ ଷ ∗ 10 = 7,11 ܰ ݉ ଷ ܴ݃ ൌ ܲ ܲܶ = 10000 0,711 ‫݂݃ܭ‬ ݉ ଷ ‫ʹכ‬ ͺͺι‫ܭ‬ = 488 ݉ ଶ ‫ݏ‬ଶ ‫ܭ‬ ߛ݃ ൌ Ͳǡ͹ͳͳ ‫݂݃ܭ‬ ݉ ଷ ൌ ߩ݃ ൌ ͲǡͲ͹ͳͳ ൌ ߩ݃ 1.19 - ) Calcular o Peso Específico do ar a 45000Kgf/m^2 (abs) e 38° C. (g=10m/s^2). ߛ௔௥ଷ଼ι஼= 45000 ∗ 9,8 287 ∗ (38 + 273) ∗ 10 = 49,4 ܰ ݉ ଷ 1.20 - ) Um volume de ͳͲ݉ ଷ de dióxido de carbono a 27°C e 13600 ௄௚௙ ௠ మ (ܾܽ‫)ݏ‬é comprimido até obter- se ʹ ݉ ଷ . Se a compressão é isotérmica qual será a pressão final? Qual a pressão final se o processo fosse adiabático? (k=1,28). Isotérmico: (ܲͳܸͳሻൌ ሺܲʹ ܸʹ ሻ ܲʹ ൌ ܲͳ൬ ܸͳ ܸʹ ൰ൌ ͳ͵ ͸ͲͲ‫כ‬ 10 2 = 68000 ‫݂݃ܭ‬ ݉ ଶ ሺܾܽ‫ݏ‬ሻ Adiabático : ܲʹ ൌ ܲͳ൬ ܸͳ ܸʹ ൰ ௞ = 13600 ∗ 10 2 ଵǡଶ଼ = 106713,78 ‫݂݃ܭ‬ ݉ ଶ ሺܾܽ‫ݏ‬ሻ
Mecânica dos Fluídos Página 14 Capitulo 2 Estática dos Fluídos 2.1 - Qual a altura da coluna de mercúrio ( ߛ‫݃ܪ‬ ൌ ͳ͵ ͸ͲͲ ௄௚௙ ௠ య ) que irá produzir na base a mesma pressão de uma coluna de água ( ߛ‫ܪ‬ଶ0 = 1000 ௄௚௙ ௠ య ) de 5m de altura. ℎ = ܲ ߛ ܲ ൌ ߛ‫ܪ‬ଶ0 ∗ ℎ ܲ ൌ ͳͲͲͲ ‫݂݃ܭ‬ ݉ ଷ ‫כ‬ͷ݉ ൌ ͷͲͲͲ ‫݂݃ܭ‬ ݉ ଶ ℎ = 5000 ‫݂݃ܭ‬ ݉ ଶ 13600 ‫݂݃ܭ‬ ݉ ଷ ൌ Ͳǡ͵ ͸͹݉ ‫ݑ݋‬͵ ͸͹݉ ݉ 2.2 - No Piezômetro inclinado da figura temos ( ߛ‫ܣ‬ ൌ ͳͲͲͲ ௄௚௙ ௠ య ), ( ߛ‫ܤ‬ ൌ ʹ ͲͲͲ ௄௚௙ ௠ య ), L1=20 cm, L2=30cm e ߙ ൌ ͵ Ͳ. Qual será a pressão atmosférica é 740m mmHg, qual o valor de P1 em mca, na escala absoluta? ܲͳ ൌ ߛ‫ͳ݄ܣ‬൅ ߛ‫ʹ݄ܤ‬ ൅ ܲ‫ݐܣ‬݉ h1 = L1 sen 30° = 0,5 * 20cm = 0,1m h2 = L2 sen 30° = 0,5 * 30cm = 0,15m P1=0,1*1000 + 0,15*2000 + 10064 P1=10464 Kgf/m^2 ou 10,46 mca
Mecânica dos Fluídos Página 15 2.3 - Calcular a pressão na câmera (1), sabendo que o pistão desloca-se com uma velocidade constante de 1,2m/S e a indicação do manômetro metálico é 0,1 Kgf/cm². Dados : D=1m; L = 0,2m; ߭×௟௘௢ = 10ିଷ ௠ మ ௦ ; Pm=0,1 Kgf/cm² ; Dp= 0,998m; δóleo = 800 Kgf/m³; v=1,2m/s; g=10m/s² . Obs.: Considerar o nível do óleo constante.
Mecânica dos Fluídos Página 16 2.4 - Determinar a pressão de 3,5 atm nas outras unidades de pressão na escala efetiva e sendo a pressão atmosférica local 740mmHg, determinar a pressão absoluta em todas unidades de pressão. Pabs = Pef + Patm Lembrando que; 1tm = 760mmHg = 10330 Kgf/m^2 = 1,033 Kgf/cm^2 = 1,01 bar = 14,7 psi = 10,33 mca 1 3,5 = ͹͸Ͳ݉ ݉ ‫݃ܪ‬ ‫ݔ‬ ֜ ‫ݔ‬ ൌ ͹͸Ͳ݉ ݉ ‫݃ܪ‬ ‫͵כ‬ ǡͷ ൌ ʹ ͸͸Ͳ݉ ݉ ‫݃ܪ‬ 1 3,5 = 10330 Kgf mଶ ‫ݔ‬ ֜ ‫ݔ‬ ൌ ͳͲ͵ ͵ Ͳ Kgf mଶ ∗ 3,5 = 36155 Kgf mଶ 1 3,5 = 1,033 ‫݂݃ܭ‬ ܿ݉ ଶ ‫ݔ‬ ֜ ‫ݔ‬ ൌ ͳǡͲ͵ ͵ ‫݂݃ܭ‬ ܿ݉ ଶ ∗ 3,5 = 3,61 ‫݂݃ܭ‬ ܿ݉ ଶ 1 3,5 = ͳǡͲͳܾܽ‫ݎ‬ ‫ݔ‬ ֜ ‫ݔ‬ ൌ ͳǡͲͳܾܽ‫ݎ‬‫͵כ‬ ǡͷ ൌ ͵ ǡͷ͵ ͷܾܽ‫ݎ‬ 1 3,5 = ͳͶǡ͹‫݅ݏ݌‬ ‫ݔ‬ ֜ ‫ݔ‬ ൌ ͳͶǡ͹‫ݏ݌‬݅‫͵כ‬ ǡͷ ൌ ͷͳǡͶͷ‫݅ݏ݌‬ 1 3,5 = ͳͲǡ͵ ͵ ݉ ܿܽ ‫ݔ‬ ֜ ‫ݔ‬ ൌ ͳͲǡ͵ ͵ ݉ ܿܽ‫͵כ‬ ǡͷ ൌ ͵ ͸ǡͳͷ݉ ܿܽ 1 3,5 = ͹͸Ͳ݉ ݉ ‫݃ܪ‬ ‫ݔ‬ ֜ ‫ݔ‬ ൌ ͹͸Ͳ݉ ݉ ‫݃ܪ‬‫͵כ‬ ǡͷ ൌ ʹ ͸͸Ͳ݉ ݉ ‫݃ܪ‬ ࡼࢋࢌ ൌ ૜Ǥ૞ࢇ࢚࢓ ൌ ૛૟૟૙࢓ ࢓ ࡴࢍ ൌ ૜૟૚૞૞ ۹܏܎ ‫ܕ‬ ૛ ൌ ૜ǡ૟૚ ࡷࢍࢌ ࢉ࢓ ૛ ൌ ૜ǡ૞૜૞࢈ࢇ࢘ൌ ૞૚ǡ૝૞࢖࢙࢏ ൌ ૜૟ǡ૚૞࢓ ࢉࢇ ͳܽ‫ݐ‬݉ ‫ݔ‬ܽ‫ݐ‬݉ = ͹͸Ͳ݉ ݉ ‫݃ܪ‬ ͹ͶͲ݉ ݉ ‫݃ܪ‬ ֜ ‫ݔ‬ ൌ ͹ͶͲ݉ ݉ ‫݃ܪ‬ ‫ͳכ‬ ͹͸Ͳ݉ ݉ ‫݃ܪ‬ ൌ ͻ͹͵ ǡ͸ͺ‫ܧ‬ െ ͵ ܽ‫ݐ‬݉ ܾܲܽ‫ݏ‬ൌ ݂ܲ݁൅ ܲܽ‫ݐ‬݉ ൌ ͻ͹͵ ǡ͸ͺ‫ܧ‬ െ ͵ ܽ‫ݐ‬݉ ൅ ͵ ǡͷ ൌ ͶǡͶ͹ܽ‫ݐ‬݉ 10330 ‫݂݃ܭ‬ ݉ ଶ ‫ݔ‬ ‫݂݃ܭ‬ ݉ ଶ = ͹͸Ͳ݉ ݉ ‫݃ܪ‬ ͹ͶͲ݉ ݉ ‫݃ܪ‬ ֜ ‫ݔ‬ ൌ ͹ͶͲ݉ ݉ ‫݃ܪ‬ ‫͵Ͳͳכ‬ ͵ Ͳ ‫݂݃ܭ‬ ݉ ଶ ͹͸Ͳ݉ ݉ ‫݃ܪ‬ = 10058 ‫݂݃ܭ‬ ݉ ଶ ܾܲܽ‫ݏ‬ൌ ݂ܲ݁൅ ܲܽ‫ݐ‬݉ ൌ ͳͲͲͷͺ ‫݂݃ܭ‬ ݉ ଶ + 36155 Kgf mଶ = 46158 Kgf mଶ 1,033 ‫݂݃ܭ‬ ܿ݉ ଶ ‫ݔ‬ ‫݂݃ܭ‬ ܿ݉ ଶ = ͹͸Ͳ݉ ݉ ‫݃ܪ‬ ͹ͶͲ݉ ݉ ‫݃ܪ‬ ֜ ‫ݔ‬ ൌ ͹ͶͲ݉ ݉ ‫݃ܪ‬ ‫ͳכ‬ǡͲ͵ ͵ ‫݂݃ܭ‬ ܿ݉ ଶ ͹͸Ͳ݉ ݉ ‫݃ܪ‬ = 1,0058 ‫݂݃ܭ‬ ܿ݉ ଶ
Mecânica dos Fluídos Página 17 ܾܲܽ‫ݏ‬ൌ ݂ܲ݁൅ ܲܽ‫ݐ‬݉ ൌ ͳǡͲͲͷͺ ‫݂݃ܭ‬ ܿ݉ ଶ + 3,61 ‫݂݃ܭ‬ ܿ݉ ଶ = 4,6158 ‫݂݃ܭ‬ ܿ݉ ଶ ͳǡͲͳܾܽ‫ݎ‬ ‫ݔ‬ܾܽ‫ݎ‬ = ͹͸Ͳ݉ ݉ ‫݃ܪ‬ ͹ͶͲ݉ ݉ ‫݃ܪ‬ ֜ ‫ݔ‬ ൌ ͹ͶͲ݉ ݉ ‫݃ܪ‬ ‫ͳכ‬ǡͲͳܾܽ‫ݎ‬ ͹͸Ͳ݉ ݉ ‫݃ܪ‬ ൌ ͻͺ͵ ǡͶʹ ‫ܧ‬ െ ͵ ܾܽ‫ݎ‬ ܾܲܽ‫ݏ‬ൌ ݂ܲ݁൅ ܲܽ‫ݐ‬݉ ൌ ͻͺ͵ ǡͶʹ ‫ܧ‬ െ ͵ ܾܽ‫ݎ‬൅ ͵ ǡͷ͵ ͷܾܽ‫ݎ‬ൌ ͶǡͷͳͺͶܾܽ‫ݎ‬ ͳͶǡ͹‫݅ݏ݌‬ ‫ݔ‬‫݅ݏ݌‬ = ͹͸Ͳ݉ ݉ ‫݃ܪ‬ ͹ͶͲ݉ ݉ ‫݃ܪ‬ ֜ ‫ݔ‬ ൌ ͹ͶͲ݉ ݉ ‫݃ܪ‬ ‫ͳכ‬Ͷǡ͹‫݅ݏ݌‬ ͹͸Ͳ݉ ݉ ‫݃ܪ‬ ൌ ͳͶǡ͵ ͳ͵ ‫݅ݏ݌‬ ܾܲܽ‫ݏ‬ൌ ݂ܲ݁൅ ܲܽ‫ݐ‬݉ ൌ ͳͶǡ͵ ͳ͵ ‫݅ݏ݌‬൅ ͷͳǡͶͷ‫݅ݏ݌‬ൌ ͸ͷǡ͹͸͵ ‫ݏ݌‬݅ ͳͲǡ͵ ͵ ݉ ܿܽ ‫ݔ‬݉ ܿܽ = ͹͸Ͳ݉ ݉ ‫݃ܪ‬ ͹ͶͲ݉ ݉ ‫݃ܪ‬ ֜ ‫ݔ‬ ൌ ͹ͶͲ݉ ݉ ‫݃ܪ‬ ‫Ͳͳכ‬ǡ͵ ͵ ݉ ܿܽ ͹͸Ͳ݉ ݉ ‫݃ܪ‬ ൌ ͳͲǡͲͷͺ݉ ܿܽ ܾܲܽ‫ݏ‬ൌ ݂ܲ݁൅ ܲܽ‫ݐ‬݉ ൌ ͳͲǡͲͷͺ݉ ܿܽ൅ ͵ ͸ǡͳͷ݉ ܿܽൌ Ͷ͸ǡʹ Ͳ݉ ܿܽ ͹͸Ͳ݉ ݉ ‫݃ܪ‬݉ ݉ ‫݃ܪ‬ ‫ݔ‬݉ ݉ ‫݃ܪ‬ = ͹͸Ͳ݉ ݉ ‫݃ܪ‬ ͹ͶͲ݉ ݉ ‫݃ܪ‬ ֜ ‫ݔ‬ ൌ ͹ͶͲ݉ ݉ ‫݃ܪ‬ ‫כ‬͹͸Ͳ݉ ݉ ‫݃ܪ‬ ͹͸Ͳ݉ ݉ ‫݃ܪ‬ ൌ ͹ͶͲ݉ ݉ ‫݃ܪ‬ ܾܲܽ‫ݏ‬ൌ ݂ܲ݁൅ ܲܽ‫ݐ‬݉ ൌ ͹ͶͲ݉ ݉ ‫݃ܪ‬ ൅ ʹ ͸͸Ͳ݉ ݉ ‫݃ܪ‬ൌ ͵ ͶͲͲ݉ ݉ ‫݃ܪ‬ ࡼࢇ࢈࢙ൌ ૝ǡ૝ૠࢇ࢚࢓ ൌ ૝૟૚૞ૡ ۹܏܎ ‫ܕ‬ ૛ ൌ ૝ǡ૟૚૞ૡ ࡷࢍࢌ ࢉ࢓ ૛ ൌ ૝ǡ૞૚ૡ૝࢈ࢇ࢘ൌ ૟૞ǡૠ૟૜࢖࢙࢏ൌ ૝૟ǡ૛૙࢓ ࢉࢇ ൌ ૜૝૙૙࢓ ࢓ ࡴࢍ 2.6 - Na figura são mostrados dois cilindros mostrados em série. Se A1 = 60cm, A2 = 20cm^2, A3=40cm^2 e F2= 1400kgf, qual a força F1 necessária para manter o equilíbrio se P1 = 70Kgf/cm^2? Somatória das forças = 0 , ou seja, F1+F2+P1=0 ‫ͳܨ‬ǯ ‫ܣ‬ ൌ ܲͳ ‫ͳܨ‬ǯൌ ൫ܲͳ(‫ͳܣ‬െ ‫ʹܣ‬ )൯ 2 ൌ ͳͶͲͲ‫݂݃ܭ‬ F1=(F1’+F2) = 1400+1400 = 2800Kgf F1=2800Kgf
Mecânica dos Fluídos Página 18 2.7 – Se o bloco de ferro no reservatório da figura repousa sem atrito com as paredes, calcular a pressão que será indicada pelos manômetros metálicos. Dados : ߛ‫ܪ‬ଶ0 = 1000 ௄௚௙ ௠ య ǡߛ‫ܨ‬௘ = 7860 ௄௚௙ ௠ య , ߛ×௟௘௢ = 900 ௄௚௙ ௠ య ܲ ൌ ߛ‫݄כ‬ ܲ ൌ ߛ‫ܪ‬ଶͲ‫݉ͲͲͳכ‬ ൌ ͳͲͲͲ ‫݂݃ܭ‬ ݉ ଷ ‫݉ͲͲͳכ‬ ൌ ͳͲ ‫݂݃ܭ‬ ܿ݉ ଶ ܲ ൌ (ߛ‫ܨ‬௘ ‫Ͳכ‬ǡͷ݉ ) ൅ ܲ‫ܽݑ݃ܣ‬ ܲ ൌ ൬͹ͺ͸Ͳ ‫݂݃ܭ‬ ݉ ଷ ‫Ͳכ‬ǡͷ൰൅ ͳͲ ‫݂݃ܭ‬ ܿ݉ ଶ = 10,4 ‫݂݃ܭ‬ ܿ݉ ଶ ܲ ൌ (ߛ×௟௘௢ ‫͵כ‬ Ͳ݉ ) ൅ ܲ‫݋ݎݎ݁ܨ‬ ܲ ൌ ൬ͻͲͲ ‫݂݃ܭ‬ ݉ ଷ ‫͵כ‬ Ͳ൰൅ ʹ ǡ͹ ‫݂݃ܭ‬ ܿ݉ ଶ = 13,1 ‫݂݃ܭ‬ ܿ݉ ଶ 2.9 – No manômetro da figura o Fluido A é a água e o B o Mercúrio. Qual a pressão de P1? Dados : ߛ‫ܪ‬ଶ0 = 1000 ௄௚௙ ௠ య ǡߛ‫ܪ‬௚ = 13600 ௄௚௙ ௠ య ܲ ൌ ߛ‫݄כ‬ ܲ ൌ ߛ‫݄כ‬ ܲͳ൅ ൬Ͳǡ͹ͷ݉ െ Ͳǡͷ݉ ‫כ‬ͳͲͲͲ ‫݂݃ܭ‬ ݉ ଷ ൰൅ ൬ͳ͵ ͸ͲͲ ‫݂݃ܭ‬ ݉ ଷ ‫Ͳכ‬ǡͷ൰ൌ ൬ͳ͵ ͸ͲͲ ‫݂݃ܭ‬ ݉ ଷ ‫Ͳכ‬ǡͳͷ݉ ൰ ܲͳ൅ (250) + ( 6800 ) = (20400) ܲͳ ൌ (20400) − (250) − ( 6800 )
Mecânica dos Fluídos Página 19 ܲͳ ൌ ͳ͵ ͵ ͵ ͷ ‫݂݃ܭ‬ ݉ ଶ 2.10 ) No manômetro diferencia da figura o fluido A é água , B é óleo e o fluído manométrico é mercúrio. Sendo h1= 25cm, h2 = 100 cm, h3 = 80cm e h4 = 10 cm, qual a diferença de pressão PA-PB? Dados : ߛ‫ܪ‬ଶ0 = 1000 ௄௚௙ ௠ య ǡߛ‫ܪ‬௚ = 13600 ௄௚௙ ௠ య ǡߛ×௟௘௢ = 800 ௄௚௙ ௠ య PA + (ߛ‫ܪ‬ଶ0 ∗ ℎ1 ) + ൫ߛ‫ܪ‬௚ ∗ ℎ2൯+ ൫ߛ‫ܪ‬௚ ∗ ℎ4൯ൌ ܲ‫ܤ‬ ൅ ൫ߛ‫ܪ‬௚ ∗ ℎ4൯൅ ሺߛ×௟௘௢ ∗ ℎ3) ܲ‫ܣ‬ ൅ ሺͳͲͲͲ ‫݂݃ܭ‬ ݉ ଷ ‫כ‬ʹ ͷ… ሻ൅ ൬ͳ͵ ͸ͲͲ ‫݂݃ܭ‬ ݉ ଷ ‫ͲͲͳכ‬… ൰൅ ൬ͳ͵ ͸ͲͲ ‫݂݃ܭ‬ ݉ ଷ ‫Ͳͳכ‬… ൰ ൌ ܲ‫ܤ‬ ൅ ൬ͳ͵ ͸ͲͲ ‫݂݃ܭ‬ ݉ ଷ ‫Ͳͳכ‬… ൰൅ ሺͺͲͲ ‫݂݃ܭ‬ ݉ ଷ ∗ 80cm) ܲ‫ܣ‬ ൅ ሺͳͲͲͲ ‫݂݃ܭ‬ ݉ ଷ ‫כ‬ʹ ͷ… ሻ൅ ൬ͳ͵ ͸ͲͲ ‫݂݃ܭ‬ ݉ ଷ ‫ͲͲͳכ‬… ൰൅ ൬ͳ͵ ͸ͲͲ ‫݂݃ܭ‬ ݉ ଷ ‫Ͳͳכ‬… ൰ ൌ ܲ‫ܤ‬ ൅ ൬ͳ͵ ͸ͲͲ ‫݂݃ܭ‬ ݉ ଷ ‫Ͳͳכ‬… ൰൅ ሺͺͲͲ ‫݂݃ܭ‬ ݉ ଷ ∗ 80cm) ܲ‫ܣ‬ ൅ ʹ ͷͲ൅ ͳ͵ ͸ͲͲ൅ ͳ͵ ͸Ͳ ൌ ܲ‫ܤ‬ ൅ ͳ͵ ͸Ͳ൅ ͸ͶͲ ܲ‫ܣ‬ െ ܲ‫ܤ‬ ൌ ͳ͵ ͸Ͳ൅ ͸ͶͲെ ʹ ͷͲെ ͳ͵ ͸ͲͲെ ͳ͵ ͸Ͳ ܲ‫ܣ‬ െ ܲ‫ܤ‬ ൌ െͳ͵ ʹ ͳͲ ‫݂݃ܭ‬ ݉ ଷ
Mecânica dos Fluídos 2.11 – Calcular a pressão na base do tanque d Dados : Pressão no fundo = Pressão no fundo = Pressão no fundo = Pressão no fundo = Calcular a pressão na base do tanque da figura se o manômetro contem água, quanto será h? Página 20 a figura se o manômetro contem água, quanto será h?

Mais conteúdo relacionado

PDF
Exercicios resolvidos de_hidraulica
porSérgio Lessa
 
PDF
Exercicios resolvidos -_hidraulica_basic
porGerson Justino
 
PDF
Solução da lista 2
porAyrton Lira
 
PDF
Aula 09 mec fluidos 2012 05
porGilson Braga
 
PDF
Hidráulica apostila 1
porFausto Afonso Domingos
 
PDF
Capitulo 4 livro
porAlexandre Davis
 
PDF
Escoamento Laminar e turbulento
porDiego Henrique
 
PPTX
6 fator de atrito
porMarilia Estevao
 
Exercicios resolvidos de_hidraulica
porSérgio Lessa
 
Exercicios resolvidos -_hidraulica_basic
porGerson Justino
 
Solução da lista 2
porAyrton Lira
 
Aula 09 mec fluidos 2012 05
porGilson Braga
 
Hidráulica apostila 1
porFausto Afonso Domingos
 
Capitulo 4 livro
porAlexandre Davis
 
Escoamento Laminar e turbulento
porDiego Henrique
 
6 fator de atrito
porMarilia Estevao
 

Mais procurados

PDF
Lista de exercicios teorema de bernoulli
porJuliana Boso Marques
 
PDF
Fluidos problemas resolvidos e propostos
porValdineilao Lao
 
PDF
Hidraúlica agrícola
porRogério Caiado Machado
 
PDF
Aula 2 componentes sistema predial de esgoto
porClaudio Santos
 
PDF
Aula 8 drenagem urbana
porJose Luis Prado Sánchez
 
PDF
Dimensionamento de Tubulações Hidraulicas
porGuilherme Camargos
 
PDF
95850647 fenomenos-de-transporte-exerc-resolv-em-04-jun-2012
porJoão Carlos Gaspar Teixeira
 
PPTX
Instalação de sistema de distribuição de gas em edificações
porRicardo Deboni
 
PDF
Aula bombas
porLuiz André
 
PPTX
Estradas
porFlavio Araujo
 
PDF
Capítulo 6
porMarcio Versuti
 
DOCX
Relatório 03 - Química Analítica Quantitativa 1 - Dosagem de AAS e Mg(OH)2
porJenifer Rigo Almeida
 
PDF
Resistencia dos-materiais-para-entender-
porMa Dos Anjos Pacheco
 
PDF
00 apresentação tubulações industriais
porLuiz Carlos Martinelli Júnior
 
PDF
Inst. agua fria predial hidraulica
porPriscilla Scura
 
PDF
Exercícios de torque
porRobsoncn
 
PDF
3. cálculo dos esforços em vigas
porWillian De Sá
 
PDF
DESENHO TÉCNICO NORMAS E PADROES
porordenaelbass
 
PDF
Exercicios de torção
porRomualdo SF
 
PDF
22 tabelas de vigas
porgabioa
 
Lista de exercicios teorema de bernoulli
porJuliana Boso Marques
 
Fluidos problemas resolvidos e propostos
porValdineilao Lao
 
Hidraúlica agrícola
porRogério Caiado Machado
 
Aula 2 componentes sistema predial de esgoto
porClaudio Santos
 
Aula 8 drenagem urbana
porJose Luis Prado Sánchez
 
Dimensionamento de Tubulações Hidraulicas
porGuilherme Camargos
 
95850647 fenomenos-de-transporte-exerc-resolv-em-04-jun-2012
porJoão Carlos Gaspar Teixeira
 
Instalação de sistema de distribuição de gas em edificações
porRicardo Deboni
 
Aula bombas
porLuiz André
 
Estradas
porFlavio Araujo
 
Capítulo 6
porMarcio Versuti
 
Relatório 03 - Química Analítica Quantitativa 1 - Dosagem de AAS e Mg(OH)2
porJenifer Rigo Almeida
 
Resistencia dos-materiais-para-entender-
porMa Dos Anjos Pacheco
 
00 apresentação tubulações industriais
porLuiz Carlos Martinelli Júnior
 
Inst. agua fria predial hidraulica
porPriscilla Scura
 
Exercícios de torque
porRobsoncn
 
3. cálculo dos esforços em vigas
porWillian De Sá
 
DESENHO TÉCNICO NORMAS E PADROES
porordenaelbass
 
Exercicios de torção
porRomualdo SF
 
22 tabelas de vigas
porgabioa
 

Destaque

PPTX
Sistemas operativos
porandres torres
 
PDF
5.node js
porGeunhyung Kim
 
PDF
by the numbers
porMatt Batchelder
 
PDF
COMO CREAR UN TEXTO
porestefania720
 
PPTX
салмина алина 1921_информатика
poralinochkavedenina
 
PPT
Renting OCNJ
porShovon Pramanik
 
PDF
Riler v California (REAL)
porCPellegrini15
 
PPTX
Perdiqua
porppcamuno
 
PPT
Tree and Binary Search tree
porMuhazzab Chouhadry
 
PPTX
Maslow's Needs
porCoombeMedia1
 
PDF
Objectives of ncert asw pdf
poraswathymaths
 
PPT
Queue in Data Structure
porMuhazzab Chouhadry
 
ODP
Els paisatges agraris (estela gil 3re) (2)
porJoan Piña Torres
 
PDF
Resolução do capítulo 3 franco brunetti
porcristian Rodrigues
 
PPTX
Ebola
poraliciadiez
 
PDF
Resolução do capítulo 1 brunetti[1]
porÍdilla Kaenna
 
PDF
Solução dos exercícios de mecânica dos fluidos franco brunetti capitulo4
porCristiano Fonseca Do Nascimento
 
PDF
Resolucao de-exercicios-cap 2 - franco-brunetti
porArgélio Paniago
 
PPTX
Alzheimer
poraliciadiez
 
Sistemas operativos
porandres torres
 
5.node js
porGeunhyung Kim
 
by the numbers
porMatt Batchelder
 
COMO CREAR UN TEXTO
porestefania720
 
салмина алина 1921_информатика
poralinochkavedenina
 
Renting OCNJ
porShovon Pramanik
 
Riler v California (REAL)
porCPellegrini15
 
Perdiqua
porppcamuno
 
Tree and Binary Search tree
porMuhazzab Chouhadry
 
Maslow's Needs
porCoombeMedia1
 
Objectives of ncert asw pdf
poraswathymaths
 
Queue in Data Structure
porMuhazzab Chouhadry
 
Els paisatges agraris (estela gil 3re) (2)
porJoan Piña Torres
 
Resolução do capítulo 3 franco brunetti
porcristian Rodrigues
 
Ebola
poraliciadiez
 
Resolução do capítulo 1 brunetti[1]
porÍdilla Kaenna
 
Solução dos exercícios de mecânica dos fluidos franco brunetti capitulo4
porCristiano Fonseca Do Nascimento
 
Resolucao de-exercicios-cap 2 - franco-brunetti
porArgélio Paniago
 
Alzheimer
poraliciadiez
 

Semelhante a Mec�nica dos fluidos

PDF
apost--mec-fluidos--109p.pdf
porCarlos Araújo Souza
 
PDF
webconferencia 1 - mecânica dos fluidos - novo.pdf
porpretoriano1982
 
DOCX
Alguns exercícios de fenômenos de transporte
porCardoso_Daiane
 
TXT
Cadernoh
porLutenchini
 
PDF
Capítulo I - Introdução à Mecânica dos Fluidos_versao_beta.pdf
porkauandias11
 
PDF
Exercicios resolvidos unidade 1 curso básico de mecânica dos fluidos
porzeramento contabil
 
PDF
Exercicios resolvidos
porTiesco
 
PDF
Exercicios resolvidos
porBenhur Demetrius de oliveira cruz
 
DOC
1ª lista de exercícios de ft
porVictoria Rodrigues
 
PPTX
EXPERIMENTAÇÃO MECÂNICA AULA 2 2022.1.pptx
porClaudio Vidal Teixeira
 
PDF
4 cinematica dos fluidos exercícios
porNathalia Salomao Damiao
 
PDF
Slides-Aula_01-Conceitos_fundamentais-PME3238.pdf
porWelkenGoncalvesCharl
 
PDF
Leis fundamentais da dinâmica dos fluidos
porSérgio Rocha
 
PDF
Cortez aula 01
porNatália Keila
 
PDF
Apostila
pormatheusmaia2407
 
PDF
2051 exercicios_mec_fluidos_nova versao - manometria exercicio 25
porSHEILA VIVIANE MARIA DOS SANTOS
 
PPT
Fisica unidade 1
porzeramento contabil
 
PDF
Mecanica_dos_Fluidos Mecãnica dos fluidos
porWilliansilva12549
 
PDF
Fisica2010
porEsquadrão Do Conhecimento
 
PDF
Lista de propriedades dos fluidos
porMarcus Freitas
 
apost--mec-fluidos--109p.pdf
porCarlos Araújo Souza
 
webconferencia 1 - mecânica dos fluidos - novo.pdf
porpretoriano1982
 
Alguns exercícios de fenômenos de transporte
porCardoso_Daiane
 
Cadernoh
porLutenchini
 
Capítulo I - Introdução à Mecânica dos Fluidos_versao_beta.pdf
porkauandias11
 
Exercicios resolvidos unidade 1 curso básico de mecânica dos fluidos
porzeramento contabil
 
Exercicios resolvidos
porTiesco
 
Exercicios resolvidos
porBenhur Demetrius de oliveira cruz
 
1ª lista de exercícios de ft
porVictoria Rodrigues
 
EXPERIMENTAÇÃO MECÂNICA AULA 2 2022.1.pptx
porClaudio Vidal Teixeira
 
4 cinematica dos fluidos exercícios
porNathalia Salomao Damiao
 
Slides-Aula_01-Conceitos_fundamentais-PME3238.pdf
porWelkenGoncalvesCharl
 
Leis fundamentais da dinâmica dos fluidos
porSérgio Rocha
 
Cortez aula 01
porNatália Keila
 
Apostila
pormatheusmaia2407
 
2051 exercicios_mec_fluidos_nova versao - manometria exercicio 25
porSHEILA VIVIANE MARIA DOS SANTOS
 
Fisica unidade 1
porzeramento contabil
 
Mecanica_dos_Fluidos Mecãnica dos fluidos
porWilliansilva12549
 
Fisica2010
porEsquadrão Do Conhecimento
 
Lista de propriedades dos fluidos
porMarcus Freitas
 

Mec�nica dos fluidos

  • 1.
    Mecânica dos FluídosPágina 1 Mecânica dos Fluidos. Prof. Engº Franco Brunetti. Resolução dos Exercícios . Por Josenei Godoi( Dúvidas,sugestões ou correções enviar email para joseneigodoi@yahoo.com.br). Resumo de fórmulas: MK*S CGS SI Fórmula ߬- Tensão de Cisalhamento Kgf/m^2 Dina/cm^2 N/m^2 ߬= ‫ܨ‬ ‫ܣ‬ μ– viscosidade Dinâmica Kgf*s/m^2 Dina*s/cm^2 N*s/m^2 ߬= ߤ ‫ݒ‬ ߝ γ – Peso Específico Kgf/m^2 Dina/cm^2 N/m^3 ߛ = ‫ܩ‬ ܸ ρ – massa específica Utm/m^3 g/cm^3 Kg/m^3 ߛ = ߩ∗ 9,8 γr – Peso espec. relativo Kgf/m^3 Dina/m^3 N/m^3 ߛ = ߛ‫ݎ‬ ߛ‫ܱ2ܪ‬ ߭– Viscosidade Dinâmica M^2/s Cm^2/s ou stoke M^2/s ߭= ߤ ߩ ܲ1 ܸ1 ܶ1 = ܲ2 ܸ2 ܶ2 ݊ = ݉ /‫ܯ‬ Nº de Mols = Massa/massa molecular ܲ ߩ = ܴܶ M=r*F (Momento = raio * Força) 1tm = 760mmHg = 10330 Kgf/m^2 = 1,033 Kgf/cm^2 = 1,01 bar = 14,7 psi = 10,33 mca Pressão efetiva é medida pelo manômetro Pressão absoluta = Pressão efetiva + pressão atmosférica ܲ = ߩ∗ ℎ A Tensão de Cisalhamento é contrária ao movimento, como se fosse uma resistência (atrito) ao fluido. ܸ݈ܽ‫ܽ݀ݎ݋‬ ‫ܽݖ݁݀݊ܽݎܩ‬ ݊ܽ‫݅݊ݑ‬݀ܽ݀݁݊‫ܽݒ݋‬ = ܸ݈ܽ‫ܽ݀ݎ݋‬ ‫ܽݖ݁݀݊ܽݎܩ‬ ݊ܽ‫݅݊ݑ‬݀ܽ݀݁‫݈݁ݒ‬ℎܽ∗ ܷ݊݅݀ܽ݀݁ܰ‫ܽݒ݋‬∗ ‫ݐܽܨ‬‫ݏݎ݁ݒ݊݋ܥ݁݀ݎ݋‬ã‫݋‬ ܷܸ݈݊݅݀ܽ݀݁݁ℎܽ
  • 2.
    Mecânica dos FluídosPágina 2 Capitulo 1 Fluidos 1.1 - ) A Massa específica de um fluído é 1200kg/m³. Determinar o seu peso específico e o peso específico relativo (g=9,8m/s²). Sendo: ρ= 1200 kg/m³ ߛ= ? g=9,8 m/s² ߛr = ? ߛ ൌ ߩ‫݃כ‬ ߛ ൌ ͳʹ ͲͲ‰Ȁ Ϳ‫ͻכ‬ǡͺ Ȁ•; ߛ ൌ ͳͳ͹͸ͲܰȀ݉ Ϳ ߛ‫ݎ‬ൌ ߛ ߛ‫ܪ‬ଶܱ Para g=10 m/s² ߛ ൌ ͳʹ ͲͲͲܰȀ݉ Ϳ sendo em SI ߛ‫ܪ‬ଶܱ ൌ ͳͲͲͲͲܰȀ݉ Ϳ ߛ‫ݎ‬ൌ ͳʹ ͲͲͲܰȀ݉ Ϳ ͳͲͲͲͲܰȀ݉ Ϳ ߛ‫ݎ‬ൌ ͳǡʹ 1.2 - ) A viscosidade cinemática de um óleo é de 0,028 m²/s e o seu peso específico relativo é de 0,85. Determinar a viscosidade cinemática nos sistemas MK*S, CGS, e SI (g=10 m/s² ) . γ=0,028 m²/s γr=0,85 μ=? ߛ ൌ ߛ‫ܪߛכݎ‬ଶܱ ߛ ൌ Ͳǡͺͷ‫כ‬ͳͲͲͲ‰ˆȀ Ϳ ߛ ൌ ͺͷͲ‰ˆȀ Ϳ ߩ ൌ ߛ ݃ ߩ ൌ 850 10 ߩ ൌ ͺͷ‫ݐݑ‬݉ Ȁ݉ Ϳ ߤ଴ ൌ ߛ଴ ‫ߩכ‬଴
  • 3.
    Mecânica dos FluídosPágina 3 ߤ଴ ൌ ͲǡͲʹ ͺ݉ ;Ȁ‫ݏ‬‫כ‬ͺͷ‫ݐݑ‬݉ Ȁ݉ Ϳ ߤ଴ ൌ ʹ ǡ͵ ͺ݂݇݃Ǥ ‫ݏ‬ ݉ ଷ Para SI: ߛ ൌ ߛ‫ܪߛכݎ‬ଶܱ ߛ ൌ Ͳǡͺͷ‫כ‬ͳͲͲͲͲȀ Ϳ ߛ ൌ ͺͷͲͲȀ Ϳ ߩ ൌ ߛ ݃ ߩ ൌ 8500 10 ߩ ൌ ͺͷͲ‫݃ܭ‬Ȁ݉ Ϳ ߤ଴ ൌ ߛ଴ ‫ߩכ‬଴ ߤ଴ ൌ ͲǡͲʹ ͺ݉ ;Ȁ‫ݏ‬‫כ‬ͺͷͲ‫݃ܭ‬Ȁ݉ Ϳ ߤ଴ ൌ ʹ ͵ ǡͺܰǤ‫ݏ‬Ȁ݉ Ϳ ߛ ൌ ͲǡͲʹ ͺ mଶ s = (0,028 ∗ (10)ଶ)ଶ cm² s = 280 cm² s ou poise Como ͳܰ ൌ ͳͲହ ݀‫݊ݕ‬ ‫׷‬ ߛ ൌ ͺͷͲͲ‫Ͳͳכ‬ହ ݀‫݊ݕ‬ (10ଶ)ଷܿ݉ Ϳ ߛ ൌ ͺͷͲ ݀‫݊ݕ‬ ܿ݉ Ϳ ߩ ൌ 850 1000 = 0,85 ݃ ܿ݉ ଷ ߤ ൌ Ͳǡͺͷ‫ʹכ‬ ͺͲ ߤ ൌ ʹ ͵ ͺ ݀݅݊ܽǤ‫ݏ‬ ܿ݉ ଶ
  • 4.
    Mecânica dos FluídosPágina 4 Ou transformando : Lembrando que : ܸ݈ܽ‫ݎ݋‬݀ܽ‫ܽݖ݁݀݊ܽݎܩ‬݊ܽ‫݅݊ݑ‬݀ܽ݀݁݊‫ܽݒ݋‬ ൌ ܸ݈ܽ‫ݎ݋‬݀ܽ‫ܽݖ݁݀݊ܽݎܩ‬݊ܽ‫݅݊ݑ‬݀ܽ݀݁‫݈݁ݒ‬݄ܽ‫כ‬ ܷ݊݅݀ܽ݀݁ܰ‫ܽݒ݋‬‫ݐܽܨכ‬‫ݎ݋‬݀݁‫ ݏݎ݁ݒ݊݋ܥ‬ ‫݋‬ ܷܸ݈݄݊݅݀ܽ݀݁݁ܽ Para SI: ߤ ൌ ʹ ǡ͵ ͺ ‫݂݃ܭ‬Ǥ‫ݏ‬ ݉ ; = 2,38 ‫݂݃ܭ‬൬ ܰ ‫ͻכ‬ǡͺ ‫݂݃ܭ‬ ൰ ݉ ; = 23,3 ܰǤ‫ݏ‬ ݉ ; Para CGS: ߤ ൌ ʹ ǡ͵ ͵ ܰǤ‫ݏ‬ ݉ ; = 2,38 ܰ ൬ ‫݅ܦ‬݊ܽ‫Ͳͳכ‬ହ ܰ ൰ ݉ ² ൬ ܿ݉ ; ‫Ͳͳכ‬ସ ݉ ² ൰ = 233 ‫݅ܦ‬݊ܽ‫ݏ‬ ܿ݉ ; ‫ݑ݋‬‫݅݋݌‬‫݁ݏ‬ 1.3 - ) A viscosidade dinâmica de um óleo é de 5 ∗ 10ିସ ௞௚௙Ǥ௦ ௠ మ e o peso específico relativo é de 0,82. Determinar a viscosidade cinemática nos sistemas MK*S SI e CGS. Considerar : g=10 m/s² e ߛ‫ܪ‬ଶܱ ൌ ͳͲͲͲ‫݂݃ܭ‬Ȁ݉ Ϳ ߛ ൌ ͷ‫Ͳͳכ‬ିଽ Kgf. s mଶ ߛ‫ݎ‬ൌ Ͳǡͺʹ ߛ ൌ ߛ‫ܪߛכݎ‬ଶܱ ߛ ൌ Ͳǡͺʹ ‫כ‬ͳͲͲͲ‰ˆȀ Ϳ ߛ ൌ ͺʹ Ͳ‰ˆȀ Ϳ ߩ ൌ ߛ ݃ ߩ ൌ 820 10 ߩ ൌ ͺʹ ‫݂݃ܭ‬Ǥ‫ݏ‬ଶ ݉ ସ ‫ݑ݋‬ ‫ݐݑ‬݉ ݉ ଷ ߭ൌ ߤ ߩ = 5 ∗ 10ିସ 82 = 6,1 ∗ 10ି଺ mଶ s MK ∗ S e SI ∴ ߭ൌ ͸ǡͳ‫Ͳͳכ‬ି଺ ∗ 10ସ = 6,1 ∗ 10ିଶ ܿ݉ ଶ ‫ݏ‬ ‫ݑ݋‬ܵ‫ݐ‬Ǥ
  • 5.
    Mecânica dos FluídosPágina 5 1.4 - ) O peso de 3dm³ de uma substância é 23,5 N. A viscosidade Cinemáica é de 10ିହ௠ మ ௦ . Se g=10 m/s² qual será a viscosidade dinâmica nos sistemas CGS, MK*S e em N. min/km² e SI? ‫ݒ‬ ൌ ͵ ݀݉ ଷ = 3 ∗ 10ିଷ ݉ ଷ Sendo : ߛ ൌ ீ ௏ ‫ݐ‬݁݉ ‫ݏ݋‬‫݁ݑݍ‬‫׷‬ ߛ ൌ ‫ܩ‬ ܸ = ʹ ͵ ǡͷܰ 3 ∗ 10ିଷ݉ ଷ = 7833 ܰ ݉ ଷ e : ߩ ൌ ߛ ݃ ߩ ൌ 7833 10 = 783,3 ‫݃ܭ‬ ݉ ଷ ߤ ൌ ߭‫ߩכ‬ ߤ ൌ ͳͲିହ ݉ ଶ ‫ݏ‬ ∗ 783,3 ‫݃ܭ‬ ݉ ଷ = 7,83 ∗ 10ିଷ ܰ ‫ݏכ‬ ݉ ଶ Lembrando que : ‫݃ܭ‬ ൌ ே ೘ ೞమ Convertendo : ܸ݈ܽ‫ݎ݋‬݀ܽ‫ܽݖ݁݀݊ܽݎܩ‬݊ܽ‫݅݊ݑ‬݀ܽ݀݁݊‫ܽݒ݋‬ ൌ ܸ݈ܽ‫ݎ݋‬݀ܽ‫ܽݖ݁݀݊ܽݎܩ‬݊ܽ‫݅݊ݑ‬݀ܽ݀݁‫݈݁ݒ‬݄ܽ‫כ‬ ܷ݊݅݀ܽ݀݁ܰ‫ܽݒ݋‬‫ݐܽܨכ‬‫ݎ݋‬݀݁‫ ݏݎ݁ݒ݊݋ܥ‬ ‫݋‬ ܷܸ݈݄݊݅݀ܽ݀݁݁ܽ Para SI: ߤ ൌ ͹ǡͺ͵ ‫Ͳͳכ‬ିଷ ܰǤ‫ݏ‬ ݉ ; = 7,83 ∗ 10ିଷ ܰ ൬ ‫݂݃ܭ‬ ܰ ∗ 9,8 ൰‫ݏכ‬ ݉ ; = 8 ∗ 10ିସ ݂݇݃‫ݏכ‬ ݉ ; Para CGS: ߤ ൌ ͹ǡͺ͵ ‫Ͳͳכ‬ିଷ ܰǤ‫ݏ‬ ݉ ; = 7,83 ∗ 10ିଷ ܰ ൬ ‫݅ܦ‬݊ܽ‫Ͳͳכ‬ହ ܰ ൰ ݉ ² ൬ ܿ݉ ; ‫Ͳͳכ‬ସ ݉ ² ൰ = 7,83 ∗ 10ିଶ ‫݅ܦ‬݊ܽ‫ݏ‬ ܿ݉ ; ‫ݑ݋‬‫݅݋݌‬‫݁ݏ‬ Para ே௠ ௜௡ ௄௠ ; : ߤ ൌ ͹ǡͺ͵ ‫Ͳͳכ‬ିଷ ܰǤ‫ݏ‬ ݉ ; = 7,83 ∗ 10ିଷ ܰ‫ݏ‬ቀ ݉ ݅݊ ‫כݏ‬͸Ͳ ቁ‫ݏכ‬ ݉ ; ൬ ‫݉ܭ‬ ଶ ݉ ଶ ∗ 10଺൰ = 130,5 ܰ݉ ݅݊ ‫݉ܭ‬ ;
  • 6.
    Mecânica dos FluídosPágina 6 1.5 - ) São dadas duas placas planas paralelas à distância de 2mm. A placa superior move-se com velocidade de 4m/s enquanto que a inferior está fixa. Se i espaço entre as dias placas dor preenchido com óleo (ν = 0,1 Stokes; ρ = 830 Kg/m³) , qual será a tensão de cisalhamento que agirá no óleo? ߬ൌ ߤ‫כ‬ ‫ݒ‬ ߝ ߥ ൌ ߤ ߩ ‫׵‬ ߤ ൌ ߥ‫כ‬ߩ ߤ ൌ Ͳǡͳ‫Ͳͳכ‬ିସ ‫כ‬ͺ͵ Ͳ ൌ ͲǡͲͲͺ͵ ܲܽ‫ݏכ‬ ߬ൌ ͲǡͲͲͺ͵ ‫כ‬ 4 2 ∗ 10ିଷ = 16,6 ܰ ݉ ଶ ‫ݑ݋‬ܲܽ 1.6-) Uma placa quadrada de 1,0m de lado e 20N de peso desliza sobre um plano inclinado de 30°, sobre uma película de óleo. A velocidade da placa é de 2m/s constante. Qual é a viscosidade dinâmica do óleo se a espessura da película é de 2mm? Sendo : ߬ൌ ߤ‫כ‬ ‫ݒ‬ ߝ ߬ൌ ߤ‫כ‬ 2 2 ∗ 10ିଷ ߬ൌ ߤ‫Ͳͳכ‬ ͵ G=20N A=1m² Θ=30° v=2m/s μ=?
  • 7.
    Mecânica dos FluídosPágina 7 Também temos : ߬ൌ ‫ܨ‬ ‫ܣ‬ = 20 cos(60°) 1 = ͳͲܰ ݉ ଶ ∴ ͳͲ ൌ ߤ‫Ͳͳכ‬ଷ ߤ ൌ ͳͲିଶ ܰǤܵ ݉ ଶ 1.7 - ) Um eixo cilíndrico vertical de diâmetro 10cm gira no interior de um mancal de diâmetro 10,005 cm. A folga entre eixo e mancal é preenchida com óleo de viscosidade dinâmica ߤ ൌ ͳͲିଶ ேǤ௦ ௠ మ . Se o mancal tem comprimento de 25cm e o eixo gira com uma rotação de 1500 rpm, qual o momento resistente à rotação?
  • 8.
    Mecânica dos FluídosPágina 8 1..8 - ) Um pistão cai dentro de um cilindro com velocidade constante de 3,2 m/s. Entre o pistão e o cilindro existe uma película de óleo de viscosidade cinemática ߥൌ ͳͲିଷ ௠ మ ௦ ݁ߛ ൌ ͺͺͲͲ ே ௠ య . Sendo o diâmetro do pistão 10cm, seu comprimento 5cm e o diâmetro do cilindro 10,2 cm , determinar o peso do pistão. (g=10m/s²). ߬ൌ ߤ‫כ‬ ‫ݒ‬ ߝ ߩ ൌ ߛ ݃ ߩ ൌ 8800 10 = 880 ‫݃ܭ‬ ݉ ଷ ߥ ൌ ߤ ߩ ‫׵‬ ߤ ൌ ߥ‫כ‬ߩ ߤ ൌ ͳͲିଷ ∗ 880 = 0,88 ܰ ݉ ଶ ߬ൌ Ͳǡͺͺ‫כ‬ 10ିଷ 0,1 ∗ 10ିଶ = 2816 ܰ ݉ ଶ ‫ܣ‬ ൌ ߨ ‫Ͳͳכ‬‫Ͳͳכ‬ିଶ ∗ 5 ∗ 10ିଶ ൌ ͷͲߨ ‫Ͳͳכ‬ିସ ߬ൌ ‫ܩ‬ ‫ܣ‬ = 2816 = ‫ܩ‬ ͷͲߨ ‫Ͳͳכ‬ିସ G = ͷͲߨ ‫Ͳͳכ‬ିସ ‫כ‬ʹ ͺͳ͸ ൌ ͶͶǡʹ ͵ ͵ ͸ܰ؆ ͶͶǡʹ ܰ ߥ ൌ ͳͲିଷ ݉ ଶ ‫ݏ‬ ߛ ൌ ͺͺͲͲ ܰ ݉ ଷ V=3,2m/s Di = 10cm L = 5cm De = 10,2cm Pp = ?
  • 9.
    Mecânica dos FluídosPágina 9 1.9 - ) O peso G da figura , ao descer gira o eixo que está apoiado em dois mancais, cilindricos de dimensões conhecidas com velocidade angular ω. Determinar o valor do peso G desprezando a rigidez e o atrito da corda e supondo que o diagrama de velocidades no lubrificante seja linear. Dados : ‫ݒ‬ ൌ ߱ ‫ݎכ‬ൌ 20 ߨ ∗ 0,1 2 = 1 ߨ ݉ ‫ݏ‬ ߬ൌ ߤ ‫ݒ‬ ߝ ߝൌ ‫݁ܦ‬െ ‫݅ܦ‬ 2 = ͲǡͳͲʹ ݉ െ ͲǡͳͲͲ݉ 2 ൌ ͲǡͲͲͳ݉ ߬ൌ ͺ‫Ͳͳכ‬ିଶ ܰǤ ‫ݏ‬ ݉ ଶ ∗ 1 ߨ ݉ ‫ݏ‬ ͲǡͲͲͳ݉ = 80 ߨ ܰȀ݉ ଶ ߬ൌ ‫ܨ‬ ‫ܣ‬ ‫ܨ‬ ൌ ߬‫ܣכ‬ ‫ܣ‬ ൌ ʹ ߨ ‫݅ܥݎכ‬݈݅݊݀‫݋ݎ‬‫ܮכ‬ ‫ܨ‬ ൌ 80 ߨ ܰ ݉ ଶ ‫ߨכ‬ ‫Ͳכ‬ǡͳ‫Ͳכ‬ǡͳ ൌ Ͳǡͺܰ ‫ܯ‬ ൌ ‫ͳܨ‬‫ܴכ‬ ൅ ‫ʹܨ‬ ‫ܴכ‬ ‫ܯ‬ ൌ ʹ ‫ͳܨ‬‫ܴכ‬ ൌ ‫ܨ‬ ‫݅ܦכ‬ ‫ܯ‬ ൌ Ͳǡͺ‫Ͳכ‬ǡͳ ൌ ͲǡͲͺͲ ‫ܯ‬ ൌ ‫ܩ‬ ‫ݎכ‬ ‫ܯ‬ ൌ Ͳǡͺ‫Ͳכ‬ǡͳ ൌ ‫ܩ‬ ‫כ‬ ‫ܦ‬ 2 ‫ܩ‬ ൌ ଴ǡ଼‫כ‬଴ǡଵ ଴ǡ଴ଵ ൌ ͺܰ ߤ = 8 ∗ 10ିଶ ܰ. ‫ݏ‬ ݉ ଶ ߱ ൌ 20 ߨ D = 0,02m De=0,102m Di = 0,100m L=0,1m
  • 10.
    Mecânica dos FluídosPágina 10 1.11 - ) Um viscosímetro de cilindros coaxiais é mostrado na figura. O cilindro externo está ligado a um eixo que transmite uma certa velocidade angular ω por meio de um motor. O Cilindro interno está suspenso por meio de um fio calibrado à torção. Quando o cilindro externo gira, devido as tensões de cisalhamento transmitidas pelo fluido, tende a girar o interno de forma a torcer o fio até que o esforço de torção no mesmo equilibre a ação das tensões de cisalhamento na periferia do cilindro interno. Sobre o fio pode estar montado um ponteiro que indicará sobre um mostrador previamente calibrado, o momento torçor aplicado. Dados: Mt= momento torçor, D1, De, ω, h, determinar a expressão que permite calcular a viscosidade do fluido à ser testado. Efetuar o problema em duas etapas: a) Desprezando o efeito do fluido; b) Levando em conta o efeito do mesmo. Onde ho = altura de líquido que causaria o mesmo efeito na base. Sugestão : considerar duas experiências com h1 e h2 diferentes, obter Mt1 e Mt2 e calcular o valor de ho. Solução : Pela lei de Newton do cisalhamento temos : ߬ൌ ߤ ݀‫ݒ‬ ݀‫ݕ‬ ൌ ߤ ‫݋ݒ‬ ߝ ‫ߤܨ‬ ‫ܣ‬ ൌ ߤ ‫݋ݒ‬ ߝ ‫ݒ‬ ൌ ߱‫ݎ‬ ‫ߤܨ‬ ൌ ‫݋ݒ‬‫ߤכ‬‫ܣכ‬ ߝ ‫ݒ‬ ൌ ߱݀݅ 2 ߝൌ ݀݁െ ݀݅ 2 ‫ܣ‬ ൌ ߨ ‫݄כ݅݀כ‬ Mt = Momento torçor ⇒ Mt – Marame = 0 ⇒ Mt = Marame
  • 11.
    Mecânica dos FluídosPágina 11 Mt = Fμ * d ‫ܯ‬ ‫ݐ‬ൌ ‫݋ݒ‬‫ߤכ‬‫ܣכ‬ ߝ ‫ܯ‬ ‫ݐ‬ൌ ߤ‫߱כ‬ ‫כ݅݀כ‬ߨ ‫݄כ݅݀כ‬‫݅݀כ‬ 2 ∗ 2 ݀݁െ ݀݅ 2 ‫ܯ‬ ‫ݐ‬ൌ ߤ‫߱כ‬ ‫݅݀כ‬ଷ ‫כ‬ߨ ‫݄כ‬ ʹ ሺ݀݁െ ݀݅ሻ A - ) ࣆ ൌ ૛࢓ ࢚ሺࢊࢋିࢊ࢏ሻ ࣓‫࢏ࢊכࢎכ࣊כ‬૜ 1.12 - ) São dados dois planos paralelos à distância de 0,5 cm. O espaço entre os dois é preenchido com um fluído de ߤ ൌ ͳͲିହ ௄௚௙‫כ‬௦ ௠ మ . Qual será a força necessária para arrastar uma chapa de espessura 0,3 colocada a igual distância dos dois, de área ͳͲͲܿ݉ ଶ à velocidade de 0,15 ௠ ௦మ. ‫ܣ‬ ൌ ͳͲͲ‫Ͳͳכ‬ିସ ݉ ଶ = 10ିଷ ݉ ଶ ‫ܨ‬ൌ ‫ܣ‬ ‫ߤכ‬‫݋ݒכ‬ ‫ܧ‬ ‫ܨ‬ൌ 10ିଷ௠ మ ∗ 10ିହ ‫݂݃ܭ‬‫ݏכ‬ ݉ ଶ ∗ 0,15 ݉ ‫ݏ‬ 1 ∗ 10ିଷ݉ = 1,5 ∗ 10ି଺ ‫݂݃ܭ‬ ‫ܨ‬ ൌ ʹ ‫כ‬ͳǡͷ‫Ͳͳכ‬ି଺ ‫݂݃ܭ‬ ‫ܨ‬ ൌ ͵ ‫כ‬ͳͲିହ ‫݂݃ܭ‬
  • 12.
    Mecânica dos FluídosPágina 12 1.13 - ) Assumindo o Diagrama de velocidades indicado na figura, no qual a parábola tem seu vértice a 10 cm do fundo, calcular o gradiente de velocidade e a tensão de cisalhamento para y=0; 5; 10cm. Adotar μ = 400 centipoises. ‫ݒ‬ ൌ ܽ‫ݕ‬ଶ ൅ ܾ‫ݕ‬൅ ܿ 1. ‫ܽݎܽ݌‬‫ݕ‬ ൌ Ͳǡͳ݉ ‫ݒ‬ ൌ ʹ ǡͷ ௠ ௦ ‫ݐݎ݋݌‬ܽ݊‫ݐ‬‫݋‬ ‫׷‬ʹ ǡͷ ൌ ܽ‫Ͳכ‬ǡͳଶ ൅ ܾ‫Ͳכ‬ǡͳ(1) 2. ‫ܽݎܽ݌‬‫ݕ‬ ൌ Ͳ‫ݒ‬ ൌ Ͳ‫ݐݎ݋݌‬ܽ݊‫ݐ‬‫݋‬ ‫׷‬ܿൌ Ͳ 3. ‫ܽݎܽ݌‬‫ݕ‬ ൌ Ͳǡͳ݉ ௗ௩ ௗ௬ ൌ Ͳ‫ݐݎ݋݌‬ܽ݊‫ݐ‬‫݋‬ ‫׷‬Ͳ ൌ ʹ ‫ܽכ‬‫Ͳכ‬ǡͳ൅ ܾൌ െͲǡʹ ܽ(2) ‫݁ܦ‬(2)݁݉ (1)ǣʹ ǡͷ ൌ ܽ‫Ͳכ‬ǡͳଶ െ Ͳǡͳ‫Ͳכ‬ǡʹ ‫ܽכ‬‫ݐݎ݋݌‬ܽ݊‫ݐ‬‫݋‬ܽൌ െʹ ͷͲ 1 ‫ܯ‬ ܵ ܾ ൌ ͷͲ ଵ ௦ ‫ݒ‬ൌ െʹ ͷͲ‫ݕ‬ଶ ൅ ͷͲ‫ݕ‬݁ ௗ௩ ௗ௬ ൌ െͷͲͲ‫ݕ‬൅ ͷͲ 1. ܲܽ‫ܽݎ‬‫ݕ‬ൌ Ͳ ௗ௩ ௗ௬ = 50 ଵ ௦ ‫ݐݎ݋݌‬ܽ݊‫ݐ‬‫݋‬ܶ ൌ ͶͲͲ‫כ‬ͳͲିଶ ∗ 50 = 200 ௗ௜௡௔ ௖௠ మ 2. ܲܽ‫ܽݎ‬‫ݕ‬ൌ ͲǡͲͷ ௗ௩ ௗ௬ = −500 ∗ 0,05 + 50 = 25 ଵ ௦ ‫ݐݎ݋݌‬ܽ݊‫ݐ‬‫݋‬ܶ ൌ ͶͲͲ‫כ‬ͳͲିଶ ∗ 25 = 100 ௗ௜௡௔ ௖௠ మ 3. ܲܽ‫ܽݎ‬‫ݕ‬ൌ Ͳǡͳ ௗ௩ ௗ௬ ൌ െͷͲͲ‫Ͳכ‬ǡͲͷ൅ ͷͲ ൌ Ͳ‫ݐݎ݋݌‬ܽ݊‫ݐ‬‫݋‬ܶ ൌ ͶͲͲ‫כ‬ͳͲିଶ ∗ 0 = 0 ௗ௜௡௔ ௖௠ మ 1.17 ) Um balão sonda de formato esférico foi projetado para ter um diâmetro de 10m a uma altitude de 45000m. Se a pressão e temperatura nesta altitude são respectivamente 2000Kgf/m^2 (abs) e -60ºC, determinar o volume de hidrogênio a 10000Kgf/m^2 (abs) e 20ºC necessário para encher o balão na terra. ܲͳ ൌ ʹ ͲͲͲ ௄௚௙ ௠ మ (ܾܽ‫)ݏ‬ ܲʹ ൌ ͳͲͲͲͲ ௄௚௙ ௠ మ (ܾܽ‫)ݏ‬ ܶͳ ൌ െ͸Ͳ͑ ‫ܥ‬ ൌ ʹ ͳ͵ ‫ܭ‬ ܶʹ ൌ െ͸Ͳ͑ ‫ܥ‬ ൌ ʹ ͻ͵ ‫ܭ‬ ܸܿൌ 4 3 ‫ߨכ‬ ‫ݎכ‬ଷ = 4 3 ‫ߨכ‬ ‫כ‬ͷଷ ܸܿൌ ͷʹ ͵ ǡͷͲ݉ ଷ ܲͳܸͳ ܶͳ = ܲʹ ܸʹ ܶʹ 2000 ‫݂݃ܭ‬ ݉ ଶ (ܾܽ‫)ݏ‬ͷʹ ͵ ǡͷͲ݉ ଷ ʹ ͳ͵ ‫ܭ‬ = 10000 ‫݂݃ܭ‬ ݉ ଶ (ܾܽ‫)ݏ‬ܸʹ ʹ ͻ͵ ‫ܭ‬ Ͷͻͳ͸ǡ͵ Ͷ‫כ‬ʹ ͻ͵ ‫ܭ‬ ൌ ͳͲͲͲͲ‫ʹܸכ‬ ܸʹ ൌ Ͷͻͳ͸ǡ͵ Ͷ‫כ‬ʹ ͻ͵ ‫ܭ‬ 10000 ܸʹ ൌ ͳͶͶǡͲͷ݉ ଷ
  • 13.
    Mecânica dos FluídosPágina 13 1.18 - ) Um gás natural tem peso específico relativo 0,6 em relação ao ar a 10000Kgf/m² (abs) e 15°C. Qual o peso deste gás nas mesmas condições de pressão e temperatura? Qual a constante R deste gás? ቀܴ௔௥ = 287 ௠ మ ௦మ௄ Ǣ݃ ൌ ͻǡͺ ௠ ௦మቁ ߛ‫ݎ‬ൌ Ͳǡ͸ ൌ ߛ‫ݏ‬ ߛܽ‫ݎ‬ = ߛ‫ݏ‬݃ ߩܽ‫ݎ‬݃ ‫ݎܣ‬൜ ܲͳ ൌ ͳͲͲͲͲ‫݂݃ܭ‬Ȁ݉ ଶ(ܾܽ‫)ݏ‬ ܶͳ ൌ ͳͷι‫ܥ‬ ൅ ʹ ͹͵ ൌ ʹ ͺͺι‫ܭ‬ ߩܽ‫ݎ‬ൌ ܲ ܴܶ = 10000 287 = 0,21 ‫ݐݑ‬݉ ݉ ଷ ߛܽ‫ݎ‬ൌ ߩܽ‫݃כݎ‬ൌ Ͳǡʹ ͳ ‫ݐݑ‬݉ ݉ ଷ ∗ 9,8 ݉ ‫ݏ‬ଶ = 1,1858 ‫݂݃ܭ‬ ݉ ଷ ߛ݃ ൌ Ͳǡ͸‫כ‬ߛܽ‫ݎ‬ൌ Ͳǡ͹ͳͳ ‫݂݃ܭ‬ ݉ ଷ ∗ 10 = 7,11 ܰ ݉ ଷ ܴ݃ ൌ ܲ ܲܶ = 10000 0,711 ‫݂݃ܭ‬ ݉ ଷ ‫ʹכ‬ ͺͺι‫ܭ‬ = 488 ݉ ଶ ‫ݏ‬ଶ ‫ܭ‬ ߛ݃ ൌ Ͳǡ͹ͳͳ ‫݂݃ܭ‬ ݉ ଷ ൌ ߩ݃ ൌ ͲǡͲ͹ͳͳ ൌ ߩ݃ 1.19 - ) Calcular o Peso Específico do ar a 45000Kgf/m^2 (abs) e 38° C. (g=10m/s^2). ߛ௔௥ଷ଼ι஼= 45000 ∗ 9,8 287 ∗ (38 + 273) ∗ 10 = 49,4 ܰ ݉ ଷ 1.20 - ) Um volume de ͳͲ݉ ଷ de dióxido de carbono a 27°C e 13600 ௄௚௙ ௠ మ (ܾܽ‫)ݏ‬é comprimido até obter- se ʹ ݉ ଷ . Se a compressão é isotérmica qual será a pressão final? Qual a pressão final se o processo fosse adiabático? (k=1,28). Isotérmico: (ܲͳܸͳሻൌ ሺܲʹ ܸʹ ሻ ܲʹ ൌ ܲͳ൬ ܸͳ ܸʹ ൰ൌ ͳ͵ ͸ͲͲ‫כ‬ 10 2 = 68000 ‫݂݃ܭ‬ ݉ ଶ ሺܾܽ‫ݏ‬ሻ Adiabático : ܲʹ ൌ ܲͳ൬ ܸͳ ܸʹ ൰ ௞ = 13600 ∗ 10 2 ଵǡଶ଼ = 106713,78 ‫݂݃ܭ‬ ݉ ଶ ሺܾܽ‫ݏ‬ሻ
  • 14.
    Mecânica dos FluídosPágina 14 Capitulo 2 Estática dos Fluídos 2.1 - Qual a altura da coluna de mercúrio ( ߛ‫݃ܪ‬ ൌ ͳ͵ ͸ͲͲ ௄௚௙ ௠ య ) que irá produzir na base a mesma pressão de uma coluna de água ( ߛ‫ܪ‬ଶ0 = 1000 ௄௚௙ ௠ య ) de 5m de altura. ℎ = ܲ ߛ ܲ ൌ ߛ‫ܪ‬ଶ0 ∗ ℎ ܲ ൌ ͳͲͲͲ ‫݂݃ܭ‬ ݉ ଷ ‫כ‬ͷ݉ ൌ ͷͲͲͲ ‫݂݃ܭ‬ ݉ ଶ ℎ = 5000 ‫݂݃ܭ‬ ݉ ଶ 13600 ‫݂݃ܭ‬ ݉ ଷ ൌ Ͳǡ͵ ͸͹݉ ‫ݑ݋‬͵ ͸͹݉ ݉ 2.2 - No Piezômetro inclinado da figura temos ( ߛ‫ܣ‬ ൌ ͳͲͲͲ ௄௚௙ ௠ య ), ( ߛ‫ܤ‬ ൌ ʹ ͲͲͲ ௄௚௙ ௠ య ), L1=20 cm, L2=30cm e ߙ ൌ ͵ Ͳ. Qual será a pressão atmosférica é 740m mmHg, qual o valor de P1 em mca, na escala absoluta? ܲͳ ൌ ߛ‫ͳ݄ܣ‬൅ ߛ‫ʹ݄ܤ‬ ൅ ܲ‫ݐܣ‬݉ h1 = L1 sen 30° = 0,5 * 20cm = 0,1m h2 = L2 sen 30° = 0,5 * 30cm = 0,15m P1=0,1*1000 + 0,15*2000 + 10064 P1=10464 Kgf/m^2 ou 10,46 mca
  • 15.
    Mecânica dos FluídosPágina 15 2.3 - Calcular a pressão na câmera (1), sabendo que o pistão desloca-se com uma velocidade constante de 1,2m/S e a indicação do manômetro metálico é 0,1 Kgf/cm². Dados : D=1m; L = 0,2m; ߭×௟௘௢ = 10ିଷ ௠ మ ௦ ; Pm=0,1 Kgf/cm² ; Dp= 0,998m; δóleo = 800 Kgf/m³; v=1,2m/s; g=10m/s² . Obs.: Considerar o nível do óleo constante.
  • 16.
    Mecânica dos FluídosPágina 16 2.4 - Determinar a pressão de 3,5 atm nas outras unidades de pressão na escala efetiva e sendo a pressão atmosférica local 740mmHg, determinar a pressão absoluta em todas unidades de pressão. Pabs = Pef + Patm Lembrando que; 1tm = 760mmHg = 10330 Kgf/m^2 = 1,033 Kgf/cm^2 = 1,01 bar = 14,7 psi = 10,33 mca 1 3,5 = ͹͸Ͳ݉ ݉ ‫݃ܪ‬ ‫ݔ‬ ֜ ‫ݔ‬ ൌ ͹͸Ͳ݉ ݉ ‫݃ܪ‬ ‫͵כ‬ ǡͷ ൌ ʹ ͸͸Ͳ݉ ݉ ‫݃ܪ‬ 1 3,5 = 10330 Kgf mଶ ‫ݔ‬ ֜ ‫ݔ‬ ൌ ͳͲ͵ ͵ Ͳ Kgf mଶ ∗ 3,5 = 36155 Kgf mଶ 1 3,5 = 1,033 ‫݂݃ܭ‬ ܿ݉ ଶ ‫ݔ‬ ֜ ‫ݔ‬ ൌ ͳǡͲ͵ ͵ ‫݂݃ܭ‬ ܿ݉ ଶ ∗ 3,5 = 3,61 ‫݂݃ܭ‬ ܿ݉ ଶ 1 3,5 = ͳǡͲͳܾܽ‫ݎ‬ ‫ݔ‬ ֜ ‫ݔ‬ ൌ ͳǡͲͳܾܽ‫ݎ‬‫͵כ‬ ǡͷ ൌ ͵ ǡͷ͵ ͷܾܽ‫ݎ‬ 1 3,5 = ͳͶǡ͹‫݅ݏ݌‬ ‫ݔ‬ ֜ ‫ݔ‬ ൌ ͳͶǡ͹‫ݏ݌‬݅‫͵כ‬ ǡͷ ൌ ͷͳǡͶͷ‫݅ݏ݌‬ 1 3,5 = ͳͲǡ͵ ͵ ݉ ܿܽ ‫ݔ‬ ֜ ‫ݔ‬ ൌ ͳͲǡ͵ ͵ ݉ ܿܽ‫͵כ‬ ǡͷ ൌ ͵ ͸ǡͳͷ݉ ܿܽ 1 3,5 = ͹͸Ͳ݉ ݉ ‫݃ܪ‬ ‫ݔ‬ ֜ ‫ݔ‬ ൌ ͹͸Ͳ݉ ݉ ‫݃ܪ‬‫͵כ‬ ǡͷ ൌ ʹ ͸͸Ͳ݉ ݉ ‫݃ܪ‬ ࡼࢋࢌ ൌ ૜Ǥ૞ࢇ࢚࢓ ൌ ૛૟૟૙࢓ ࢓ ࡴࢍ ൌ ૜૟૚૞૞ ۹܏܎ ‫ܕ‬ ૛ ൌ ૜ǡ૟૚ ࡷࢍࢌ ࢉ࢓ ૛ ൌ ૜ǡ૞૜૞࢈ࢇ࢘ൌ ૞૚ǡ૝૞࢖࢙࢏ ൌ ૜૟ǡ૚૞࢓ ࢉࢇ ͳܽ‫ݐ‬݉ ‫ݔ‬ܽ‫ݐ‬݉ = ͹͸Ͳ݉ ݉ ‫݃ܪ‬ ͹ͶͲ݉ ݉ ‫݃ܪ‬ ֜ ‫ݔ‬ ൌ ͹ͶͲ݉ ݉ ‫݃ܪ‬ ‫ͳכ‬ ͹͸Ͳ݉ ݉ ‫݃ܪ‬ ൌ ͻ͹͵ ǡ͸ͺ‫ܧ‬ െ ͵ ܽ‫ݐ‬݉ ܾܲܽ‫ݏ‬ൌ ݂ܲ݁൅ ܲܽ‫ݐ‬݉ ൌ ͻ͹͵ ǡ͸ͺ‫ܧ‬ െ ͵ ܽ‫ݐ‬݉ ൅ ͵ ǡͷ ൌ ͶǡͶ͹ܽ‫ݐ‬݉ 10330 ‫݂݃ܭ‬ ݉ ଶ ‫ݔ‬ ‫݂݃ܭ‬ ݉ ଶ = ͹͸Ͳ݉ ݉ ‫݃ܪ‬ ͹ͶͲ݉ ݉ ‫݃ܪ‬ ֜ ‫ݔ‬ ൌ ͹ͶͲ݉ ݉ ‫݃ܪ‬ ‫͵Ͳͳכ‬ ͵ Ͳ ‫݂݃ܭ‬ ݉ ଶ ͹͸Ͳ݉ ݉ ‫݃ܪ‬ = 10058 ‫݂݃ܭ‬ ݉ ଶ ܾܲܽ‫ݏ‬ൌ ݂ܲ݁൅ ܲܽ‫ݐ‬݉ ൌ ͳͲͲͷͺ ‫݂݃ܭ‬ ݉ ଶ + 36155 Kgf mଶ = 46158 Kgf mଶ 1,033 ‫݂݃ܭ‬ ܿ݉ ଶ ‫ݔ‬ ‫݂݃ܭ‬ ܿ݉ ଶ = ͹͸Ͳ݉ ݉ ‫݃ܪ‬ ͹ͶͲ݉ ݉ ‫݃ܪ‬ ֜ ‫ݔ‬ ൌ ͹ͶͲ݉ ݉ ‫݃ܪ‬ ‫ͳכ‬ǡͲ͵ ͵ ‫݂݃ܭ‬ ܿ݉ ଶ ͹͸Ͳ݉ ݉ ‫݃ܪ‬ = 1,0058 ‫݂݃ܭ‬ ܿ݉ ଶ
  • 17.
    Mecânica dos FluídosPágina 17 ܾܲܽ‫ݏ‬ൌ ݂ܲ݁൅ ܲܽ‫ݐ‬݉ ൌ ͳǡͲͲͷͺ ‫݂݃ܭ‬ ܿ݉ ଶ + 3,61 ‫݂݃ܭ‬ ܿ݉ ଶ = 4,6158 ‫݂݃ܭ‬ ܿ݉ ଶ ͳǡͲͳܾܽ‫ݎ‬ ‫ݔ‬ܾܽ‫ݎ‬ = ͹͸Ͳ݉ ݉ ‫݃ܪ‬ ͹ͶͲ݉ ݉ ‫݃ܪ‬ ֜ ‫ݔ‬ ൌ ͹ͶͲ݉ ݉ ‫݃ܪ‬ ‫ͳכ‬ǡͲͳܾܽ‫ݎ‬ ͹͸Ͳ݉ ݉ ‫݃ܪ‬ ൌ ͻͺ͵ ǡͶʹ ‫ܧ‬ െ ͵ ܾܽ‫ݎ‬ ܾܲܽ‫ݏ‬ൌ ݂ܲ݁൅ ܲܽ‫ݐ‬݉ ൌ ͻͺ͵ ǡͶʹ ‫ܧ‬ െ ͵ ܾܽ‫ݎ‬൅ ͵ ǡͷ͵ ͷܾܽ‫ݎ‬ൌ ͶǡͷͳͺͶܾܽ‫ݎ‬ ͳͶǡ͹‫݅ݏ݌‬ ‫ݔ‬‫݅ݏ݌‬ = ͹͸Ͳ݉ ݉ ‫݃ܪ‬ ͹ͶͲ݉ ݉ ‫݃ܪ‬ ֜ ‫ݔ‬ ൌ ͹ͶͲ݉ ݉ ‫݃ܪ‬ ‫ͳכ‬Ͷǡ͹‫݅ݏ݌‬ ͹͸Ͳ݉ ݉ ‫݃ܪ‬ ൌ ͳͶǡ͵ ͳ͵ ‫݅ݏ݌‬ ܾܲܽ‫ݏ‬ൌ ݂ܲ݁൅ ܲܽ‫ݐ‬݉ ൌ ͳͶǡ͵ ͳ͵ ‫݅ݏ݌‬൅ ͷͳǡͶͷ‫݅ݏ݌‬ൌ ͸ͷǡ͹͸͵ ‫ݏ݌‬݅ ͳͲǡ͵ ͵ ݉ ܿܽ ‫ݔ‬݉ ܿܽ = ͹͸Ͳ݉ ݉ ‫݃ܪ‬ ͹ͶͲ݉ ݉ ‫݃ܪ‬ ֜ ‫ݔ‬ ൌ ͹ͶͲ݉ ݉ ‫݃ܪ‬ ‫Ͳͳכ‬ǡ͵ ͵ ݉ ܿܽ ͹͸Ͳ݉ ݉ ‫݃ܪ‬ ൌ ͳͲǡͲͷͺ݉ ܿܽ ܾܲܽ‫ݏ‬ൌ ݂ܲ݁൅ ܲܽ‫ݐ‬݉ ൌ ͳͲǡͲͷͺ݉ ܿܽ൅ ͵ ͸ǡͳͷ݉ ܿܽൌ Ͷ͸ǡʹ Ͳ݉ ܿܽ ͹͸Ͳ݉ ݉ ‫݃ܪ‬݉ ݉ ‫݃ܪ‬ ‫ݔ‬݉ ݉ ‫݃ܪ‬ = ͹͸Ͳ݉ ݉ ‫݃ܪ‬ ͹ͶͲ݉ ݉ ‫݃ܪ‬ ֜ ‫ݔ‬ ൌ ͹ͶͲ݉ ݉ ‫݃ܪ‬ ‫כ‬͹͸Ͳ݉ ݉ ‫݃ܪ‬ ͹͸Ͳ݉ ݉ ‫݃ܪ‬ ൌ ͹ͶͲ݉ ݉ ‫݃ܪ‬ ܾܲܽ‫ݏ‬ൌ ݂ܲ݁൅ ܲܽ‫ݐ‬݉ ൌ ͹ͶͲ݉ ݉ ‫݃ܪ‬ ൅ ʹ ͸͸Ͳ݉ ݉ ‫݃ܪ‬ൌ ͵ ͶͲͲ݉ ݉ ‫݃ܪ‬ ࡼࢇ࢈࢙ൌ ૝ǡ૝ૠࢇ࢚࢓ ൌ ૝૟૚૞ૡ ۹܏܎ ‫ܕ‬ ૛ ൌ ૝ǡ૟૚૞ૡ ࡷࢍࢌ ࢉ࢓ ૛ ൌ ૝ǡ૞૚ૡ૝࢈ࢇ࢘ൌ ૟૞ǡૠ૟૜࢖࢙࢏ൌ ૝૟ǡ૛૙࢓ ࢉࢇ ൌ ૜૝૙૙࢓ ࢓ ࡴࢍ 2.6 - Na figura são mostrados dois cilindros mostrados em série. Se A1 = 60cm, A2 = 20cm^2, A3=40cm^2 e F2= 1400kgf, qual a força F1 necessária para manter o equilíbrio se P1 = 70Kgf/cm^2? Somatória das forças = 0 , ou seja, F1+F2+P1=0 ‫ͳܨ‬ǯ ‫ܣ‬ ൌ ܲͳ ‫ͳܨ‬ǯൌ ൫ܲͳ(‫ͳܣ‬െ ‫ʹܣ‬ )൯ 2 ൌ ͳͶͲͲ‫݂݃ܭ‬ F1=(F1’+F2) = 1400+1400 = 2800Kgf F1=2800Kgf
  • 18.
    Mecânica dos FluídosPágina 18 2.7 – Se o bloco de ferro no reservatório da figura repousa sem atrito com as paredes, calcular a pressão que será indicada pelos manômetros metálicos. Dados : ߛ‫ܪ‬ଶ0 = 1000 ௄௚௙ ௠ య ǡߛ‫ܨ‬௘ = 7860 ௄௚௙ ௠ య , ߛ×௟௘௢ = 900 ௄௚௙ ௠ య ܲ ൌ ߛ‫݄כ‬ ܲ ൌ ߛ‫ܪ‬ଶͲ‫݉ͲͲͳכ‬ ൌ ͳͲͲͲ ‫݂݃ܭ‬ ݉ ଷ ‫݉ͲͲͳכ‬ ൌ ͳͲ ‫݂݃ܭ‬ ܿ݉ ଶ ܲ ൌ (ߛ‫ܨ‬௘ ‫Ͳכ‬ǡͷ݉ ) ൅ ܲ‫ܽݑ݃ܣ‬ ܲ ൌ ൬͹ͺ͸Ͳ ‫݂݃ܭ‬ ݉ ଷ ‫Ͳכ‬ǡͷ൰൅ ͳͲ ‫݂݃ܭ‬ ܿ݉ ଶ = 10,4 ‫݂݃ܭ‬ ܿ݉ ଶ ܲ ൌ (ߛ×௟௘௢ ‫͵כ‬ Ͳ݉ ) ൅ ܲ‫݋ݎݎ݁ܨ‬ ܲ ൌ ൬ͻͲͲ ‫݂݃ܭ‬ ݉ ଷ ‫͵כ‬ Ͳ൰൅ ʹ ǡ͹ ‫݂݃ܭ‬ ܿ݉ ଶ = 13,1 ‫݂݃ܭ‬ ܿ݉ ଶ 2.9 – No manômetro da figura o Fluido A é a água e o B o Mercúrio. Qual a pressão de P1? Dados : ߛ‫ܪ‬ଶ0 = 1000 ௄௚௙ ௠ య ǡߛ‫ܪ‬௚ = 13600 ௄௚௙ ௠ య ܲ ൌ ߛ‫݄כ‬ ܲ ൌ ߛ‫݄כ‬ ܲͳ൅ ൬Ͳǡ͹ͷ݉ െ Ͳǡͷ݉ ‫כ‬ͳͲͲͲ ‫݂݃ܭ‬ ݉ ଷ ൰൅ ൬ͳ͵ ͸ͲͲ ‫݂݃ܭ‬ ݉ ଷ ‫Ͳכ‬ǡͷ൰ൌ ൬ͳ͵ ͸ͲͲ ‫݂݃ܭ‬ ݉ ଷ ‫Ͳכ‬ǡͳͷ݉ ൰ ܲͳ൅ (250) + ( 6800 ) = (20400) ܲͳ ൌ (20400) − (250) − ( 6800 )
  • 19.
    Mecânica dos FluídosPágina 19 ܲͳ ൌ ͳ͵ ͵ ͵ ͷ ‫݂݃ܭ‬ ݉ ଶ 2.10 ) No manômetro diferencia da figura o fluido A é água , B é óleo e o fluído manométrico é mercúrio. Sendo h1= 25cm, h2 = 100 cm, h3 = 80cm e h4 = 10 cm, qual a diferença de pressão PA-PB? Dados : ߛ‫ܪ‬ଶ0 = 1000 ௄௚௙ ௠ య ǡߛ‫ܪ‬௚ = 13600 ௄௚௙ ௠ య ǡߛ×௟௘௢ = 800 ௄௚௙ ௠ య PA + (ߛ‫ܪ‬ଶ0 ∗ ℎ1 ) + ൫ߛ‫ܪ‬௚ ∗ ℎ2൯+ ൫ߛ‫ܪ‬௚ ∗ ℎ4൯ൌ ܲ‫ܤ‬ ൅ ൫ߛ‫ܪ‬௚ ∗ ℎ4൯൅ ሺߛ×௟௘௢ ∗ ℎ3) ܲ‫ܣ‬ ൅ ሺͳͲͲͲ ‫݂݃ܭ‬ ݉ ଷ ‫כ‬ʹ ͷ… ሻ൅ ൬ͳ͵ ͸ͲͲ ‫݂݃ܭ‬ ݉ ଷ ‫ͲͲͳכ‬… ൰൅ ൬ͳ͵ ͸ͲͲ ‫݂݃ܭ‬ ݉ ଷ ‫Ͳͳכ‬… ൰ ൌ ܲ‫ܤ‬ ൅ ൬ͳ͵ ͸ͲͲ ‫݂݃ܭ‬ ݉ ଷ ‫Ͳͳכ‬… ൰൅ ሺͺͲͲ ‫݂݃ܭ‬ ݉ ଷ ∗ 80cm) ܲ‫ܣ‬ ൅ ሺͳͲͲͲ ‫݂݃ܭ‬ ݉ ଷ ‫כ‬ʹ ͷ… ሻ൅ ൬ͳ͵ ͸ͲͲ ‫݂݃ܭ‬ ݉ ଷ ‫ͲͲͳכ‬… ൰൅ ൬ͳ͵ ͸ͲͲ ‫݂݃ܭ‬ ݉ ଷ ‫Ͳͳכ‬… ൰ ൌ ܲ‫ܤ‬ ൅ ൬ͳ͵ ͸ͲͲ ‫݂݃ܭ‬ ݉ ଷ ‫Ͳͳכ‬… ൰൅ ሺͺͲͲ ‫݂݃ܭ‬ ݉ ଷ ∗ 80cm) ܲ‫ܣ‬ ൅ ʹ ͷͲ൅ ͳ͵ ͸ͲͲ൅ ͳ͵ ͸Ͳ ൌ ܲ‫ܤ‬ ൅ ͳ͵ ͸Ͳ൅ ͸ͶͲ ܲ‫ܣ‬ െ ܲ‫ܤ‬ ൌ ͳ͵ ͸Ͳ൅ ͸ͶͲെ ʹ ͷͲെ ͳ͵ ͸ͲͲെ ͳ͵ ͸Ͳ ܲ‫ܣ‬ െ ܲ‫ܤ‬ ൌ െͳ͵ ʹ ͳͲ ‫݂݃ܭ‬ ݉ ଷ
  • 20.
    Mecânica dos Fluídos 2.11– Calcular a pressão na base do tanque d Dados : Pressão no fundo = Pressão no fundo = Pressão no fundo = Pressão no fundo = Calcular a pressão na base do tanque da figura se o manômetro contem água, quanto será h? Página 20 a figura se o manômetro contem água, quanto será h?