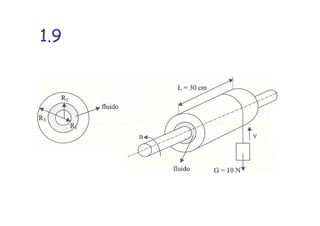
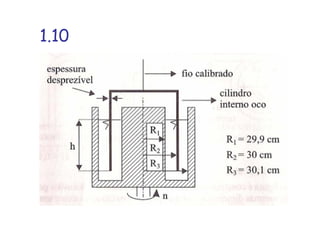
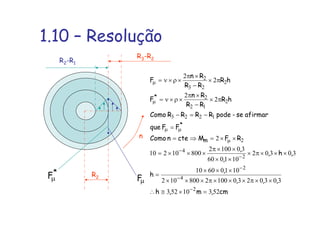
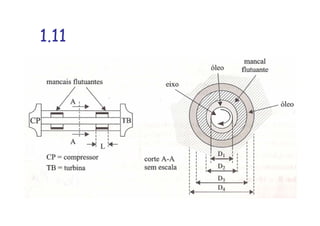
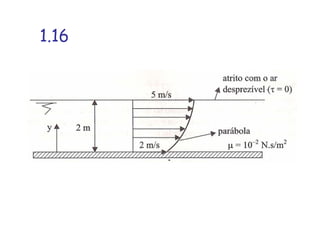
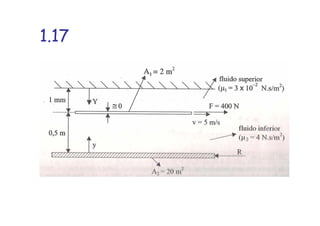
1. O documento apresenta as resoluções de 21 exercícios propostos no livro do Professor Brunetti sobre exercícios de física e mecânica. 2. As resoluções envolvem cálculos com unidades como força, velocidade, densidade e outros para chegar às respostas corretas. 3. Os exercícios tratam de temas como cinemática, dinâmica, hidrostática e hidrodinâmica.

1. Exercícios propostos
Livro do Prof. Brunetti
Exercícios 1.1 – 1.3 – 1.5

2. 1.1 - Resolução

3. 1.1 – Resolução (cont)

4. 1.2 – Resolução
St)ou(
s
cm
,,
SI)eSMK(
s
m
,
)
m
skgf
ou(
m
utm
g
m
kgf
,
*
4
2
Hr
2
246
2
6
4
3
302
1016101016
1016
82
105
82
10
820
8201000820
−−
−
−
×=××=ν
×≅
×
=
ρ
µ
=ν
×
==
γ
=ρ
=×=γ×γ=γ

5. 1.3 - Resolução

6. 1.3 – Resolução (cont.)

7. 1.4 - Resolução
Pa)ou(
m
N
,,
v
sPa,,
23
4
616
102
4
00830
008308301010
=
×
×=
ε
×µ=τ
×=××=ρ×ν=µ∴
ρ
µ
=ν
−
−

8. 1.5 -

9. Resolução

10. 1.6

11. 1.6 - Resolução
s
m
,
,,
,,
v
,,
)(
v
10100,5
:se-temrepousoemcilindrooSupondo
4-
122
050090800010
1050101050
050090
2
1091010
8000
4
2
2
≅
××π××
××××
=∴
××π×
×−
××=×
−
−
−

12. 1.7

13. Resolução

14. 1.8

15. 1.8 - Resolução
3
2
21
2
2
2
21
16800
320020000408020000
10
802000080
80
80
4040
40
2
1010
2
10
10
m
N
L
4
0,1
L,
V
A
V)(AVV
:quese-temVVe
V
G
Como
AGG
ATGeAGT
AA
,
FF
L
4
0,1
VeL,A
2
22
2221
21
1
1
2
=γ
+γ=∴×+γ=
×
×π
××π
×+γ=∴×+γ=γ
÷×+×γ=×γ
==γ
×+=∴
×+=×+=
×=×
×
×==
×
×π
=××π=
−
−
µµ

16. 1.9

17. Resolução

18. 1.10

19. 1.10 – Resolução
R2
R3-R2
n
µF
*
Fµ
R2-R1
cm,m,h
,,,
,
h
,h,
,
,
RFMctenComo
FFque
afirmarse-podeRRRRComo
hR
RR
Rn
F
hR
RR
Rn
F
m
*
*
52310523
30302301002800102
10106010
30302
101060
301002
80010210
2
2
2
2
2
2
4
2
2
4
2
1223
2
12
2
2
23
2
=×≅∴
××π×××π×××
×××
=
×××π×
××
××π
×××=
××=⇒=
=
−=−
π×
−
×π
×ρ×ν=
π×
−
×π
×ρ×ν=
−
−
−
−
−
µ
µµ
µ
µ

20. 1.11

21. Resolução

22. 1.12

23. 1.12 - Resolução
G
T
MOV
cFµ
cte
s
m
v == 2
NT
,
)
,
(
T
LD
v
GFGT ic
48
2
50
10
2
50250
2
1050
2
3
=∴
π
××π×
×
−
×−=
π
ε
µ−=−=
−
−
µ

24. 1.12 – Resolução (cont.)
Nm,,,M
MMMaigualseráquemotorseja,ourotação,dadireçãona
Mmomentoumexistirdevequeconcluirse-podeMMComo
Nm,
,
,
)
,
(
D
FM
Nm,
,d
TM
2
i
104252
52
2
502
50
10
2
50250
10
10
2
42
2
10
48
2
1
12
2
3
2
1
=−=
−=
>
=×
π
××π×
×
−
×=×=
=×=×=
−
−
µ
s
m
v
v *
*
10
255
2
=∴=
µF
2
iD
T
2
d
2
d
T ×
n
*
v
2
iD
F ×µ

25. 1.13

26. 1.13 - Resolução

27. 1.14

28. 1.14 – Resolução
001040005010500
1002510400
1
2550050500050
2005010400
1
50
5050050
1
50
1
2502010
2010200
1010521
2
2
2
2
2
2
2
=××=τ∴=+×−=⇒=
=××=τ∴=+×−=⇒=
=××=τ∴=⇒=
+−=+=⇒=∴
−=∴××−×=
−=∴+××=∴=⇒=
=∴=⇒=
×+×=∴=⇒=
++=
−
−
−
,
dy
dv
0,1mypara
cm
dina
s
,
dy
dv
m,ypara
cm
dina
sdy
dv
0ypara
y
dy
dv
ey-250yv
s
b
ms
aa,,0,1a2,5:(1)em(2)De
(2)a,bb,a
dy
dv
0,1mypara3)
0c0v0ypara2)
(1),b,a,
s
m
2,5v0,1mypara)
cbyayv
2
2

29. 1.15

30. 1.15 - Resolução

31. 1.16

32. 1.16 - Resolução
2
2
2
2
030310
1
3351
23750
1
3
1
7504
2
43
42200
2
43
2225
2
m
N
,
dy
dv
e
sdy
dv
que0yparay,
dy
dv
b)
memye
s
m
emvcomyy,v
s
b
ms
,aa
a
:(2)e(1)De
(2)abba
dy
dv
2mypara
(1)
a
bba
s
m
5v2mypara
s
m
c
s
m
2v0ypara
a)
=×=×µ=τ==⇒+−=
++−=
=∴−=⇒−=
−
−=⇒+××=∴=⇒=
−
=⇒+×+×=∴=⇒=
=∴=⇒=
−

33. 1.17

34. Resolução

35. Resolução (cont.)

36. 1.18 - Resolução
%,%
)()(%
3217
100
323287
200000
293287
150000
323287
200000
100
1
21
≅ρ∆
×
×
×
−
×=×
ρ
ρ−ρ
=ρ∆

37. 1.19 - Resolução

38. 1.20 - Resolução
338
44910
27338287
441000
m
N
,
)(C
ar ≅×
+×
=γ o

39. 1.21 - Resolução