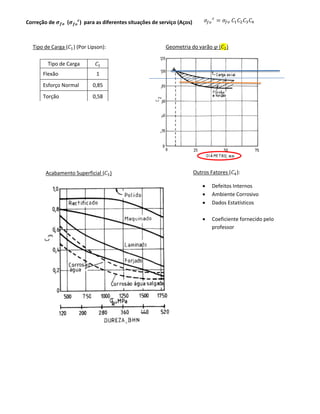
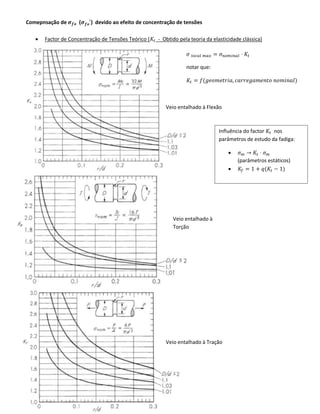
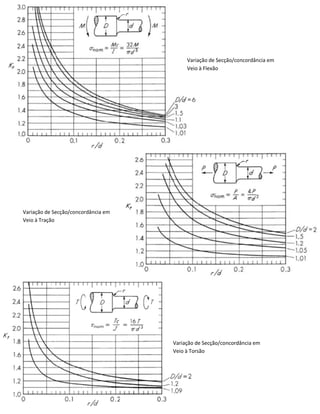
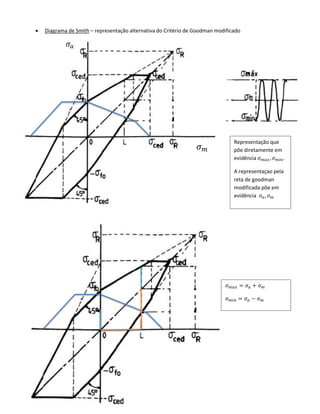
O documento discute metodologias práticas para o dimensionamento à fadiga de materiais, focando em curvas S-N que relacionam a tensão (σa) com o número de ciclos até a falha. São apresentadas fórmulas e critérios de dimensionamento, incluindo Soderberg e Goodman, além de fatores de correção relacionados à geometria do material, acabamento superficial e condições de carga. O conceito de tensão estática equivalente também é introduzido, fornecendo uma comparação entre solicitações dinâmicas e estáticas.