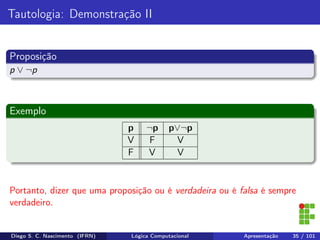
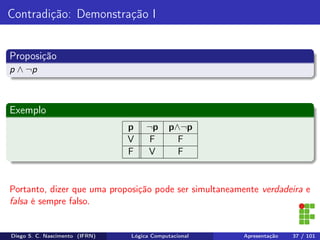
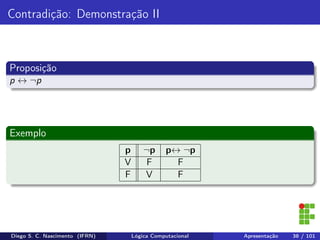
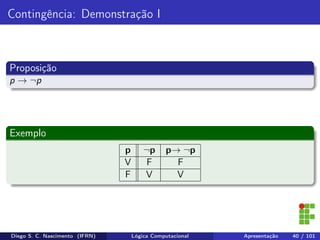
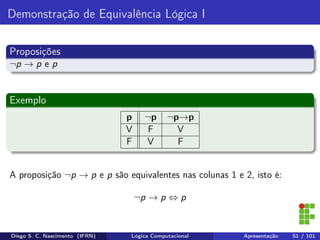
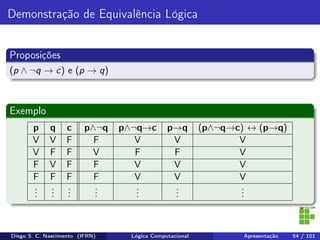
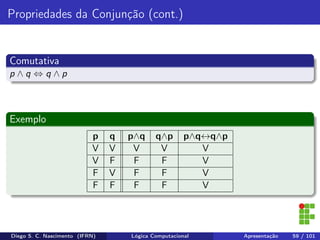
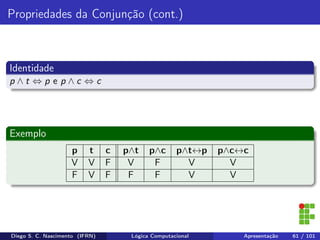
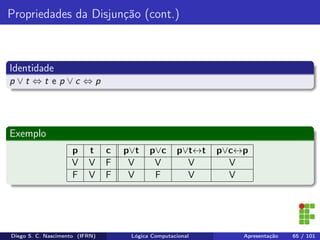
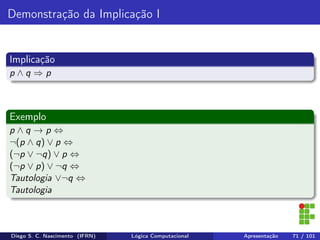
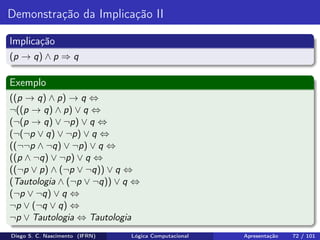
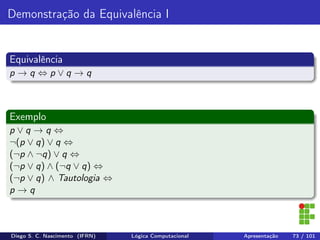
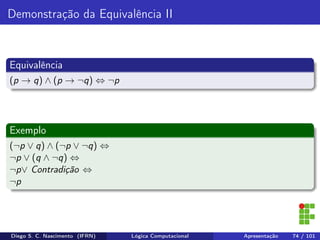
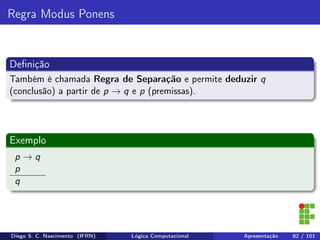
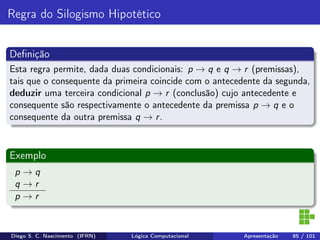
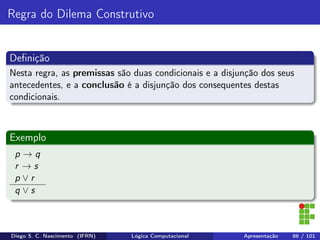
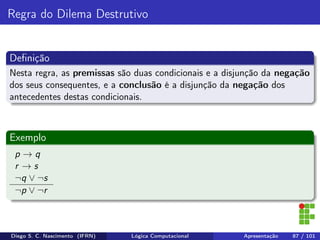
O documento apresenta uma introdução ao curso de Lógica Computacional ministrado por Diego Silveira Costa Nascimento no Instituto Federal do Rio Grande do Norte. A ementa do curso inclui tópicos como lógica proposicional, tabelas-verdade, implicação e equivalência lógica, método dedutivo e lógica de predicados. O documento também discute conceitos fundamentais da lógica como proposições, conectivos lógicos, negação, conjunção, disjunção, condicional e bicondicional