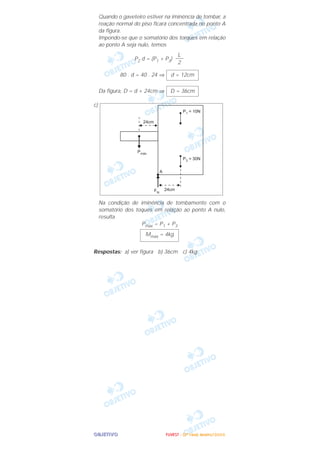
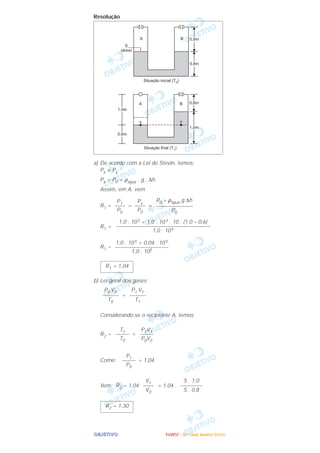
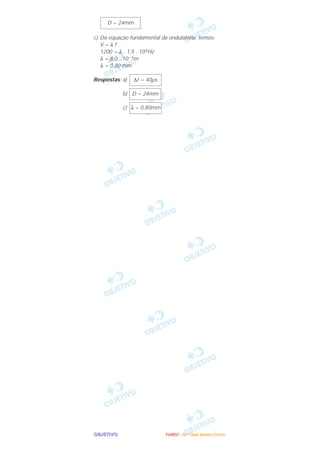
O documento apresenta cinco problemas de física resolvidos. O primeiro problema trata de uma pista de skate e calcula a velocidade do skatista, a altura máxima alcançada e a distância necessária entre as rampas. O segundo problema analisa as condições de equilíbrio de um gaveteiro. O terceiro calcula forças e velocidades envolvidas no movimento de um elevador suspenso. O quarto determina características ópticas de uma lente projetora. E o quinto analisa mudanças de pressão e temper