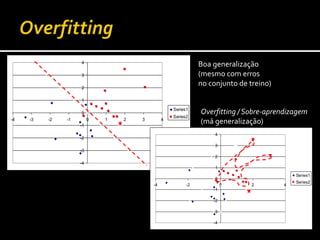
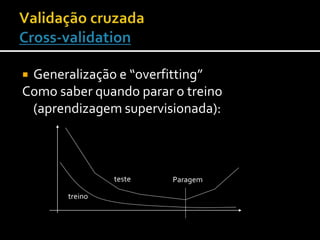
O documento discute conceitos fundamentais de aprendizagem automática, incluindo generalização versus overfitting, avaliação de modelos em conjuntos de treino e teste, e validação cruzada para evitar overfitting. Ele também explica como calcular e interpretar intervalos de confiança para comparar resultados de modelos.

1. Mestrado em Engenharia Informática

2.  Generalização e Overfitting
 Avaliação de hipóteses e comparação de
resultados
30/01/2015 Aprendizagem Automática / Machine Learning 2

3.  Até que ponto a nossa hipótese ira ter o
resultado correcto para exemplos fora do
conjunto de treino?
30/01/2015 Aprendizagem Automática / Machine Learning 3

4. -4
-3
-2
-1
0
1
2
3
4
-4 -3 -2 -1 0 1 2 3 4
Series1
Series2
-4
-3
-2
-1
0
1
2
3
4
-4 -2 0 2 4
Series1
Series2
Boa generalização
(mesmo com erros
no conjunto de treino)
Overfitting / Sobre-aprendizagem
(má generalização)

5.  Generalização e “overfitting”
Como saber quando parar o treino
(aprendizagem supervisionada):
treino
teste Paragem

6.  Validação => três conjuntos de dados:
◦ Treino,Teste,Validação
 Conjuntos pequenos (k-fold validation/leave n-off)
1. Dividir dados em k subconjuntos
2. Em cada uma de k experiências usar um dos conjuntos para validação
3. Calcular nº médio de iterações (n) para minimizar erro de validação
4. Treinar com todos os dados n épocas

7.  Cada teste dá um resultado (erro médio, qualidade média,
etc.) X = {x1, x2, …, xn}
 Um conjunto de testes terá também um média (bem como
variância e desvio-padrão)
 Média (mean)
 Variância (variance)
 O desvio padrão
(standard deviation)


n
i
ix
n
X
1
1




n
i
i Xx
n
Xs
1
2
)(
1
1
)(


n
i
i Xx
n
X
1
2
)(
1
)(
7AA/ML, Luís Nunes, DCTI/ISCTE

8.  Um intervalo de confiança de C%, diz-nos que, com C% de probabilidade, a média
real (para um número infinito de experiências) estará no intervalo definido por
n é o número de experiências realizadas
t a distribuiçãoT-student, parametrizada por C,n.
Ex: O intervalo de confiança de 95%, para um erro médio de 0.1, com variância 0.01,
para 30 experiências:
Excel:TINV(1 – C, n-1) =TINV(1 - 0.95, 29) = 2.04
n
s(X)tX,
n
s(X)– tX nC,nC, 




2.04t95,30 
 0.1037250.096275,
30
0.012.040.1,
30
0.012.04–0.1 


 
8AA/ML, Luís Nunes, DCTI/ISCTE

9.  Para provar (com uma certeza razoável) que
um método é melhor que outro é necessário
que os intervalos de confiança de ambas as
experiências não se sobreponham
9AA/ML, Luís Nunes, DCTI/ISCTE

10.  http://en.wikipedia.org/wiki/Student's_t-test
30/01/2015 Aprendizagem Automática / Machine Learning 10

11.  Generalização e Overfitting
 Avaliação de hipóteses e comparação de
resultados
30/01/2015 Aprendizagem Automática / Machine Learning 11