Este documento apresenta uma introdução ao Machine Learning usando a biblioteca scikit-learn em Python. Ele discute conceitos básicos de aprendizagem supervisionada e não-supervisionada, modelos como regressão linear, KNN, SVM, PCA e K-Means e técnicas como seleção de modelo e validação cruzada.

1. Machine Learning usando scikits.learnMarcelo Gomes Pereira de LacerdaEngenharia da ComputaçãoEscola Politécnica de PernambucoUniversidade de PernambucoPUG-PE - Julho de 2011

2. RoteiroElementos BásicosAprendizagem SupervisionadaSeleção de ModeloAprendizagem Não-SupervisionadaConclusãoPUG-PE - Julho de 2011

3. Elementos BásicosBase de dados (features = Array 2D, labelsArray 1D)EstimatorEvaluatorPUG-PE - Julho de 2011

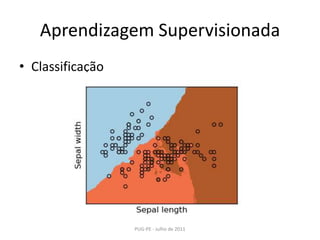
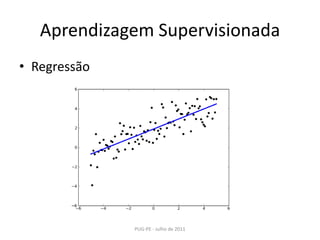
4. Aprendizagem SupervisionadaEncontrar relação entre dois datasets: X e YA aprendizagem ocorre sob “orientações” do humano, o qual diz se uma resposta dada pelo modelo está correta ou não e qual a resposta certa.X => Array 2D. Ex.: [[1,2,3],[3,4,5],[5,6,7]]Y => Array 1D (na maioria dos casos). Ex.: [0,0,1]fit(X,Y)predict(p)PUG-PE - Julho de 2011

5. Aprendizagem SupervisionadaClassificaçãoPUG-PE - Julho de 2011

6. Aprendizagem SupervisionadaRegressãoPUG-PE - Julho de 2011

7. K-NearestNeighborClassifier (KNN)PUG-PE - Julho de 2011

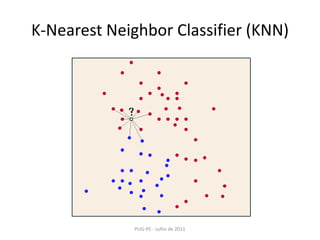
8. K-NearestNeighborClassifier (KNN)PUG-PE - Julho de 2011import numpy as npfrom scikits.learn import datasetsiris = datasets.load_iris()iris_X = iris.datairis_y = iris.targetnp.random.seed(0)indices = np.random.permutation(len(iris_X))iris_X_train = iris_X[indices[:-10]]iris_y_train = iris_y[indices[:-10]]iris_X_test = iris_X[indices[-10:]]iris_y_test = iris_y[indices[-10:]]

9. K-NearestNeighborClassifier (KNN)PUG-PE - Julho de 2011fromscikits.learn.neighborsimportNeighborsClassifierknn = NeighborsClassifier()printknn.fit(iris_X_train, iris_y_train)NeighborsClassifier(n_neighbors=5, window_size=1, algorithm=auto)printknn.predict(iris_X_test)array([1, 2, 1, 0, 0, 0, 2, 1, 2, 0])

10. Regressão Lineary = xb + ey = variável alvox = dadob = coeficientee = ruído da observaçãoPUG-PE - Julho de 2011

11. Regressão LinearPUG-PE - Julho de 2011fromscikits.learnimportlinear_modeldiabetes = datasets.load_diabetes()diabetes_X_train = diabetes.data[:-20]diabetes_X_test = diabetes.data[-20:]diabetes_y_train = diabetes.target[:-20]diabetes_y_test = diabetes.target[-20:]regr = linear_model.LinearRegression()regr.fit(diabetes_X_train, diabetes_y_train)regr.predict(diabetes_X_test)[1,2.6,-1.67,3,...,2.45]

12. Regressão para ClassificaçãoRegressão Linear não é recomendadaDá muito peso a elementos distantes da fronteira de decisão!Solução: Regressão Logística (Sigmóide)PUG-PE - Julho de 2011

13. Regressão para ClassificaçãoPUG-PE - Julho de 2011logistic = linear_model.LogisticRegression(C=1e5)logistic.fit(iris_X_train, iris_y_train)LogisticRegression(C=100000.0, intercept_scaling=1, dual=False, fit_intercept=True, penalty='l2', tol=0.0001)

14. SupportVector Machines (SVM)Achar a combinação de amostras de treinamento de forma que maximize a margem entre as classesPUG-PE - Julho de 2011

15. SupportVector Machines (SVM)SVC = SupportVectorClassificationSVR = SupportVectorRegressionPUG-PE - Julho de 2011fromscikits.learnimportsvmsvc = svm.SVC(kernel='linear')svc.fit(iris_X_train, iris_y_train)

16. SupportVector Machines (SVM)Outros Kernelssvc = svm.SVC(kernel='linear')svc = svm.SVC(kernel='poly',degree=3)svc = svm.SVC(kernel='rbf')PUG-PE - Julho de 2011

17. Seleção de ModeloPUG-PE - Julho de 2011

18. Seleção de Modelo Medição da qualidade de predição do modelo através do método scoreDica: Implementar K-FoldCrossValidation para obter resultados mais precisos.PUG-PE - Julho de 2011>>> fromscikits.learnimportdatasets, svm>>> digits = datasets.load_digits()>>> X_digits = digits.data>>> y_digits = digits.target>>> svc = svm.SVC()>>> svc.fit(X_digits[:-100], y_digits[:-100]).score(X_digits[-100:], y_digits[-100:])0.97999999999999998

19. Seleção de ModeloPUG-PE - Julho de 2011>>> importnumpy as np>>> X_folds = np.array_split(X_digits, 10)>>> y_folds = np.array_split(y_digits, 10)>>> scores = list()>>> for k in range(10):... X_train = list(X_folds)... X_test = X_train.pop(k)... X_train = np.concatenate(X_train)... y_train = list(y_folds)... y_test = y_train.pop(k)... y_train = np.concatenate(y_train)... scores.append(svc.fit(X_train, y_train).score(X_test, y_test))>>> printscores[0.9555555555555556, 1.0, 0.93333333333333335, 0.99444444444444446, 0.98333333333333328, 0.98888888888888893, 0.99444444444444446, 0.994413407821229, 0.97206703910614523, 0.96089385474860334]

20. Seleção de ModeloO scikits.learn dá uma mãozinha!Ou... Melhor ainda!PUG-PE - Julho de 2011>>> kfold = cross_val.KFold(len(X_digits), k=3)>>> [svc.fit(X_digits[train], y_digits[train]).score(X_digits[test], y_digits[test])... for train, test in kfold][0.95530726256983245, 1.0, 0.93296089385474856, 0.98324022346368711, 0.98882681564245811, 0.98882681564245811, 0.994413407821229, 0.994413407821229, 0.97206703910614523, 0.95161290322580649]>>> cross_val.cross_val_score(svc, X_digits, y_digits, cv=kfold, n_jobs=-1)array([ 0.95530726, 1., 0.93296089, 0.98324022, 0.98882682, 0.98882682, 0.99441341, 0.99441341, 0.97206704, 0.9516129 ])

21. Seleção de ModeloCross-ValidationGeneratorsKFold(n, k)StratifiedKFold(y, k)LeaveOneOut(n)LeaveOneLabelOut(labels)PUG-PE - Julho de 2011

22. Aprendizagem Não-SupervisionadaPUG-PE - Julho de 2011

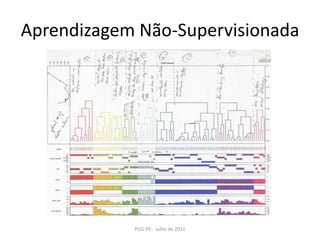
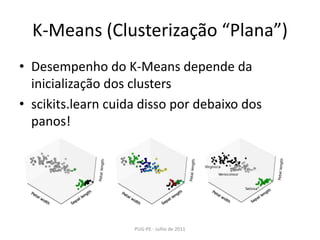
23. K-Means (Clusterização “Plana”)PUG-PE - Julho de 2011>>> fromscikits.learnimport cluster, datasets>>> iris = datasets.load_iris()>>> X_iris = iris.data>>> y_iris = iris.target>>> k_means = cluster.KMeans(k=3)>>> k_means.fit(X_iris) KMeans(verbose=0, k=3, max_iter=300, init='k-means++',...>>> printk_means.labels_[::10][1 1 1 1 1 0 0 0 0 0 2 2 2 2 2]>>> printy_iris[::10][0 0 0 0 0 1 1 1 1 1 2 2 2 2 2]

24. K-Means (Clusterização “Plana”)Desempenho do K-Means depende da inicialização dos clustersscikits.learn cuida disso por debaixo dos panos!PUG-PE - Julho de 2011

25. PCA (Principal Componente Analysis)PUG-PE - Julho de 2011

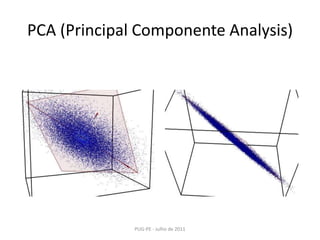
26. PCA (Principal Componente Analysis)PUG-PE - Julho de 2011>>> x1 = np.random.normal(size=100)>>> x2 = np.random.normal(size=100)>>> x3 = x1 + x2>>> X = np.c_[x1, x2, x3]>>> fromscikits.learnimportdecomposition>>> pca = decomposition.PCA()>>> pca.fit(X)>>> printpca.explained_variance_[ 2.77227227e+00, 1.14228495e+00, 2.66364138e-32]>>> X_reduced = pca.fit_transform(X, n_components=2)>>> X_reduced.shape(100, 2)

27. ConclusãoPUG-PE - Julho de 2011 =

28. Fontehttp://gaelvaroquaux.github.com/scikit-learn-tutorial/PUG-PE - Julho de 2011

29. OBRIGADO!PUG-PE - Julho de 2011