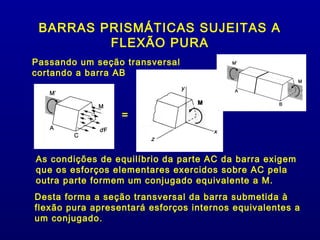
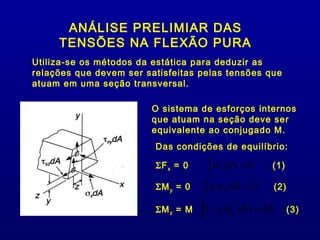
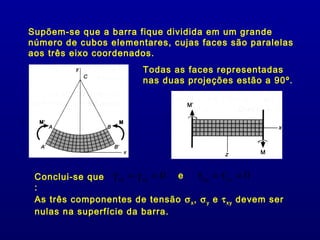
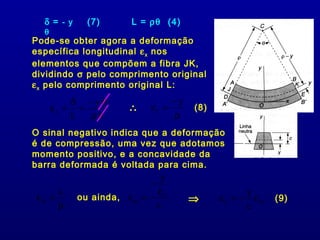
1) O documento discute flexão pura em barras prismáticas, onde momentos iguais e opostos são aplicados no mesmo plano longitudinal, causando curvatura uniforme. 2) É analisado o estado de tensões em uma seção transversal sob flexão pura, que resulta em um estado uniaxial de tensão com a tensão variando linearmente através da espessura. 3) A superfície onde a tensão é zero é chamada de superfície neutra.

1. RESISTÊNCIA DOS
MATERIAIS
FLEXÃO PURA

2. INTRODUÇÃO
Considere um membro prismático (barra) submetido a
dois conjugados ou momentos, iguais e de sentidos
opostos, atuando no mesmo plano longitudinal.
Assim, para o caso em questão é dito que o membro
está sob FLEXÃO PURA.
PURA

3. BARRAS PRISMÁTICAS SUJEITAS A
FLEXÃO PURA
Passando um seção transversal
cortando a barra AB
=
As condições de equilíbrio da parte AC da barra exigem
que os esforços elementares exercidos sobre AC pela
outra parte formem um conjugado equivalente a M.
Desta forma a seção transversal da barra submetida à
flexão pura apresentará esforços internos equivalentes a
um conjugado.

4. ANÁLISE PRELIMIAR DAS
TENSÕES NA FLEXÃO PURA
Utiliza-se os métodos da estática para deduzir as
relações que devem ser satisfeitas pelas tensões que
atuam em uma seção transversal.
O sistema de esforços internos
que atuam na seção deve ser
equivalente ao conjugado M.
Das condições de equilíbrio:
ΣF x = 0 ∫ σ dA = 0 (1)
x
ΣM y = 0 ∫ z σ dA = 0 (2)
x
ΣM z = M ∫ (− y σ )dA = M (3)
x

5. DEFORMAÇÕES EM UMA BARRA
SIMÉTRICA NA FLEXÃO PURA
Analisa-se as deformações em uma barra prismática que
contém um plano de simetria.
A barra se flexiona sob a ação
dos conjugados, mas
permanece simétrica em
relação ao plano.
O momento fletor é o mesmo
em qualquer seção, a barra se
flexiona de modo uniforme.
A linha AB, segundo a face superior da barra intercepta
o plano de conjugados, tem uma curvatura constante.
O mesmo acontece com a linha A’B’, na face inferior.

6. Supõem-se que a barra fique dividida em um grande
número de cubos elementares, cujas faces são paralelas
aos três eixo coordenados.
Todas as faces representadas
nas duas projeções estão a 90º.
Conclui-se que γ xy = γ xz = 0 e τ xy = τ xz = 0
:
As três componentes de tensão σ x , σ y e τ xy devem ser
nulas na superfície da barra.

7. Portanto, a única componente de tensão que não se
anula é a componente normal σ x .
Desse modo, em qualquer ponto de uma barra esbelta
submetida à flexão pura, tem-se um estado uniaxial de
tensões.
Lembrando que quando M > 0, a linha AB diminui de
comprimento e a linha A’B’ aumenta de comprimento,
verifica-se que a deformação específica ε x e a tensão
σ x são negativas na parte superior da barra
(compressão) e positivas na parte inferior (tração).
Deve haver então uma superfície paralela à face
superior e à face inferior da barra, onde ε x e σ x se
tornam nulas . Esta superfície é chamada de superfície
neutra.
neutra

8. A superfície neutra intercepta
o plano de simetria ao longo de
um arco de circunferência DE.
Pode-se escrever:
L = ρθ (4)
Considerando que o arco JK
está localizado acima da
superfície neutra, tem-se para
L’:
L’ = (ρ - y) θ (5)
Como o comprimento original
do arco JK era L:
δ = L’ - L (6)
ou
δ = (ρ - y) θ - ρ θ = - y (7)
θ

9. δ = - y (7) L = ρθ (4)
θ
Pode-se obter agora a deformação
específica longitudinal ε x nos
elementos que compõem a fibra JK,
dividindo σ pelo comprimento original
ε x pelo comprimento original L: (8)
δ −yθ −y
εx = = ∴ εx = (8)
L ρθ ρ
O sinal negativo indica que a deformação
é de compressão, uma vez que adotamos
momento positivo, e a concavidade da
barra deformada é voltada para cima.
y
−
c εx y
εm = ou ainda, ε m = ⇒ εx = − εm (9)
ρ c c