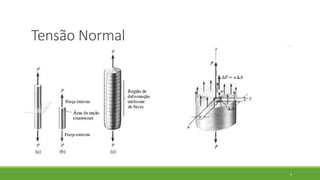
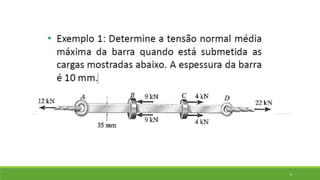
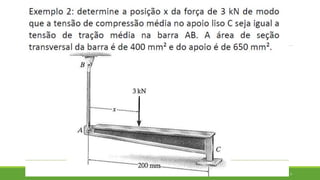
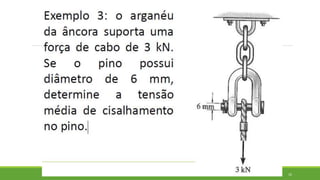
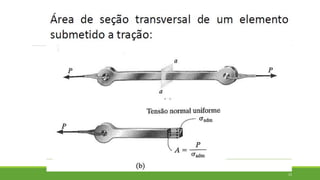
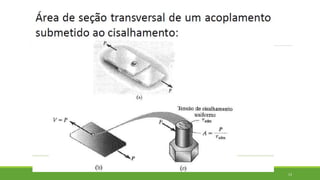
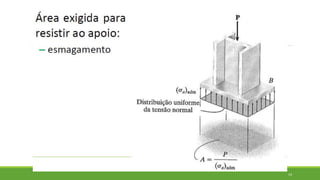
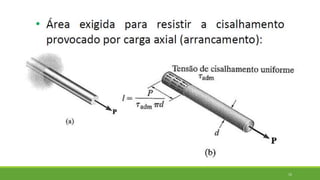
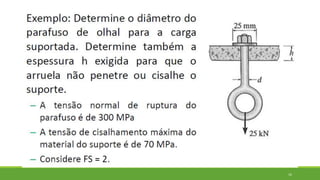
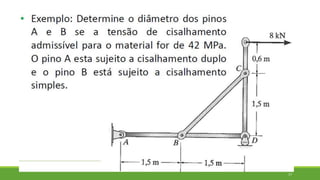
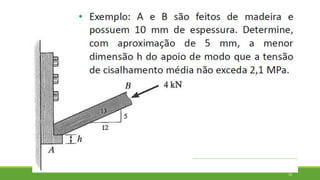
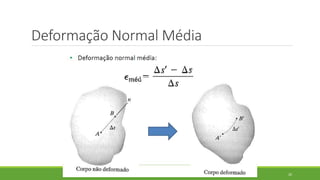
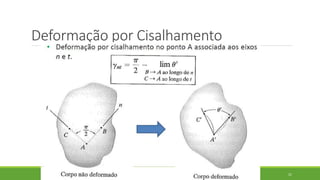
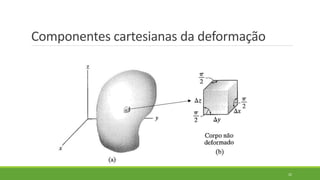
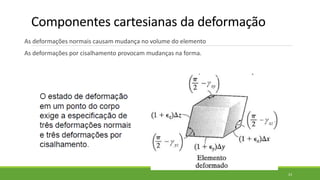
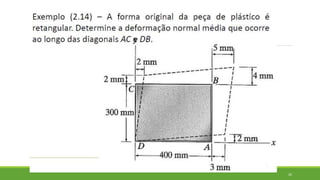
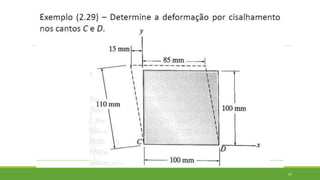
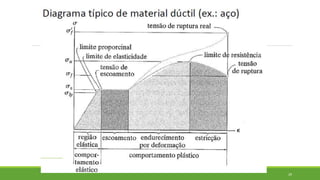
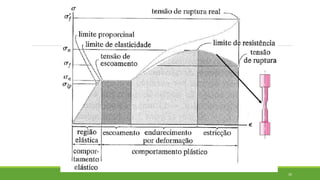
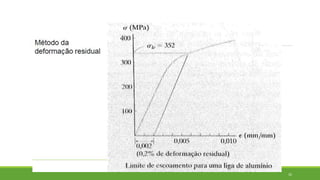
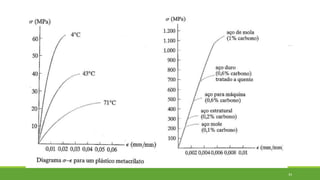
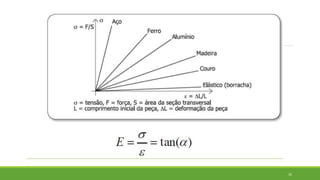
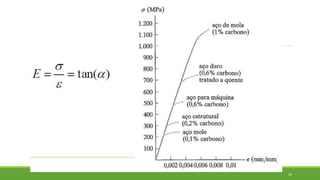
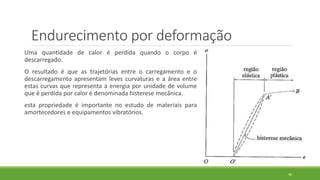
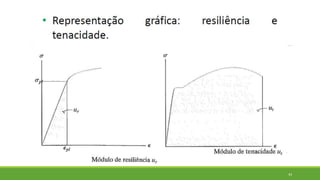
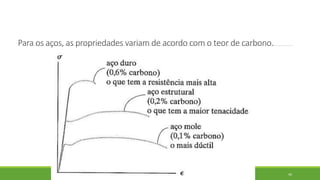
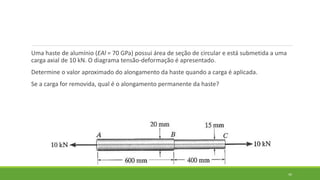
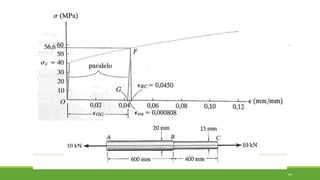
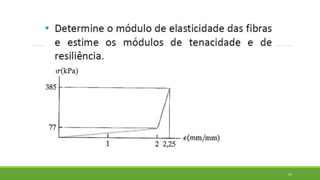
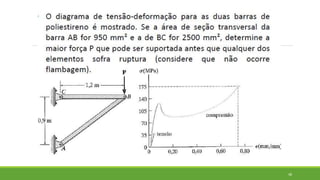
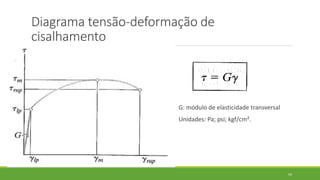
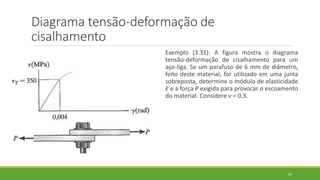
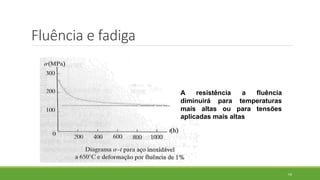
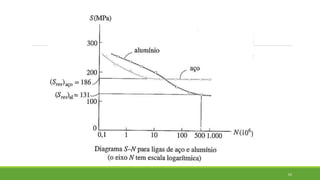
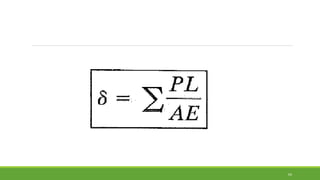
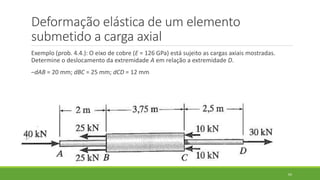
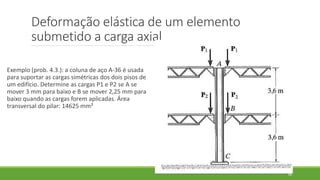
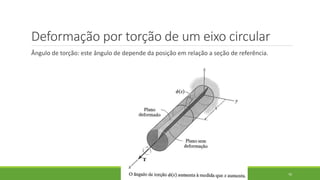
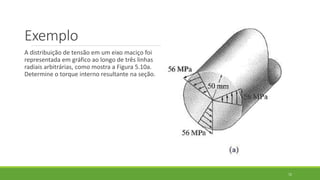
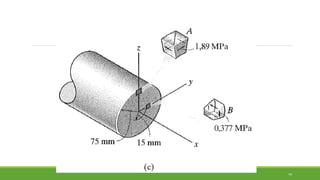
Este documento discute conceitos de resistência dos materiais como tensão normal, tensão cisalhante, deformação, propriedades dos materiais, diagramas tensão-deformação, e equipamentos estáticos. Inclui exemplos e exercícios sobre cálculos de tensão, deformação, módulo de elasticidade e dimensões de barras sob carga axial.

1. Equipamentos Estáticos
Faculdade Multivix
CIARA BARCELOS ZANELATO

2. Conhecimentos prévios
Resistencia dos Materiais;
Dinâmica aplicada à máquinas
2

3. 3

4. Introdução...
Equipamentos estáticos: o que são?
Por que estuda-los?
O que iremos aprender?
Trabalho “Braçal”, cálculos e
muitos exercícios;
Qual minha contribuição como
engenheiro mecânico?
VAMOS LÁ?
4

5. Tensão Normal
5

6. 6

7. 7

8. Tensão cisalhante Simples
8

9. Tensão Cisalhante Dupla
9

10. 10

11. A escora de madeira mostrada na Figura está suspensa por uma haste
de aço de 10 mm de diâmetro que está presa na parede.
Considerando que a escora suporta uma carga vertical de 5 kN,
calcule a tensão de cisalhamento média na haste na parede e ao
longo dos dois planos sombreados da escora, um dos quais é indicado
como abcd.
11

12. 12

13. 13

14. 14

15. 15

16. 16

17. 17

18. 18

19. DEFORMAÇÃO
19

20. Deformação Normal Média
20

21. Deformação por Cisalhamento
21

22. Componentes cartesianas da deformação
22

23. Componentes cartesianas da deformação
As deformações normais causam mudança no volume do elemento
As deformações por cisalhamento provocam mudanças na forma.
23

24. Análise de pequenas deformações
A maioria dos projetos de engenharia envolve aplicações para as quais somente são permitidas
pequenas deformações:
Deformações normais são muito pequenas e comparação com a unidade (ϵ << 1).
Ângulos de deformação por cisalhamento são pequenos o suficiente para permitir aproximações
matemáticas como sen θ = θ e tg θ = θ.
Alguns elementos apresentam deformações tão pequenas em relação a outros que podem ser
considerados como rígidos, pelo menos em parte da análise.
24

25. 25

26. 26

27. 27

28. Propriedades dos Materiais
28

29. 29

30. 30

31. Materiais dúcteis
São materiais que apresentam grandes deformações antes da ruptura (principalmente na região
de escoamento)
A ductilidade de um material pode ser expressa em termos da porcentagem de alongamento
(deformação de ruptura em porcentagem) ou da porcentagem de redução de área:
31

32. 32

33. Materiais frágeis
Estes materiais exibem pouco ou nenhum escoamento antes da falha.
A tensão ruptura por tração não é bem definida, pois o surgimento de trincas iniciais no corpo se
mostra bastante aleatório.
Os materiais frágeis apresentam uma resistência à compressão axial muito mais alta que à
tração.
33

34. 34

35. 35

36. 36

37. Exercício
Uma haste de poliestireno, de comprimento de 300 mm e diâmetro de 25,4 mm, é submetida a
uma carga de tração de 3560 N. Sabendo que E = 3,1 GPa, determine:
–O alongamento da haste;
–A tensão normal na haste;
37

38. Uma barra de alumínio de 1,5 m de comprimento não poderá alongar-se mais do que 1 mm e a
tensão normal não pode exceder a 40 Mpa, quando estiver submetida a uma carga axial de 3 kN.
Sabendo que E = 70 GPa, determine o diâmetro necessário da barra.
38

39. Endurecimento por deformação
Se um corpo de prova de um material dúctil for
solicitado na região plástica, e então o
carregamento for retirado, a deformação elástica é
recuperada, porém a deformação plástica
permanece.
•O material passará a ter um ponto de
escoamento mais alto, porém uma região plástica
menor.
39

40. Endurecimento por deformação
Uma quantidade de calor é perdida quando o corpo é
descarregado.
O resultado é que as trajetórias entre o carregamento e o
descarregamento apresentam leves curvaturas e a área entre
estas curvas que representa a energia por unidade de volume
que é perdida por calor é denominada histerese mecânica.
esta propriedade é importante no estudo de materiais para
amortecedores e equipamentos vibratórios.
40

41. Energia de Deformação
41

42. Energia de Deformação
A resiliência de um material representa sua capacidade de absorver energia sem sofrer
qualquer dano permanente.
Módulo de tenacidade: representa a densidade de energia absorvida pelo material antes da
ruptura.
Esta propriedade é muito importante no projeto de elementos estruturais e de máquinas que
possam estar submetidos as carregamentos acidentais.
42

43. 43

44. Para os aços, as propriedades variam de acordo com o teor de carbono.
44

45. Uma haste de alumínio (EAl = 70 GPa) possui área de seção de circular e está submetida a uma
carga axial de 10 kN. O diagrama tensão-deformação é apresentado.
Determine o valor aproximado do alongamento da haste quando a carga é aplicada.
Se a carga for removida, qual é o alongamento permanente da haste?
45

46. 46

47. 47

48. 48

49. Coeficiente de Poisson
Quando submetido a uma força axial, um corpo deformável não apenas altera sua dimensão
axial, mas também suas dimensões transversais.
49

50. 50

51. Para maioria dos materiais sólidos não porosos o
valor de ν encontra se entre 0,25 e 0,33.
O valor máximo possível para o coeficiente de
Poisson é 0,5.
51

52. Coeficiente de Poisson
Exemplo (3.29): a figura mostra a porção elástica do
diagrama tensão deformação para um aço liga. O
corpo de prova do qual ela foi obtida tinha um
diâmetro de original de 13 mm e comprimento de
referência de 50 mm. Quando a carga aplicada ao
corpo de prova for de 50 kN, o diâmetro é de
12,99265 mm. Determine o coeficiente de Poisson
para o material.
52

53. Diagrama tensão-deformação de
cisalhamento
O comportamento de um material submetido ao cisalhamento puro pode ser estudado a partir
de ensaios com corpos de prova na forma de tubos de parede fina submetidos a carga de torção.
A partir do torque e do ângulo de torção (medidos experimentalmente), pode-se calcular a
tensão de cisalhamento e a deformação angular.
Os resultados podem ser relacionados na forma de um diagrama tensão-deformação de
cisalhamento, que vai apresentar muitas características semelhantes a já vistas.
53

54. Diagrama tensão-deformação de
cisalhamento
G: módulo de elasticidade transversal
Unidades: Pa; psi; kgf/cm².
54

55. Diagrama tensão-deformação de
cisalhamento
As três constantes do material E, ν e G estão relacionadas pela equação:
Uma vez que E e G podem ser determinados experimentalmente, o coeficiente de Poisson é
determinado por esta equação.
55

56. Diagrama tensão-deformação de
cisalhamento
Exemplo (3.31): A figura mostra o diagrama
tensão-deformação de cisalhamento para um
aço-liga. Se um parafuso de 6 mm de diâmetro,
feito deste material, for utilizado em uma junta
sobreposta, determine o módulo de elasticidade
E e a força P exigida para provocar o escoamento
do material. Considere ν = 0,3.
56

57. Fluência e fadiga
Fluência: é a deformação permanente dependente do tempo que ocorrem nos materiais
submetidos a grandes tensões ou altas temperaturas.
Em alguns materiais, a taxa de fluência é dependente da temperatura. Ex.: metais e materiais
cerâmicos.
Em outros materiais, a taxa de fluência é mais dependente do nível de tensão aplicado. Ex.:
concreto e madeira
57

58. Fluência e fadiga
Quando a fluência é importante no projeto, é considerado o limite de fluência, que representa o
valor de tensão inicial mais alta que o material pode suportar durante um tempo específico sem
apresentar determinada deformação por fluência.
Uma forma de determinar o limite de fluência é aplicar simultaneamente tensões diferentes em
corpos de prova e observar o tempo necessário para a ocorrência de certa deformação por
fluência
58

59. Fluência e fadiga
A resistência a fluência
diminuirá para temperaturas
mais altas ou para tensões
aplicadas mais altas
59

60. Fluência e fadiga
Fadiga é a redução da resistência de um material quando
submetido a ciclos repetitivos de tensão e deformação.
Devido a fadiga, a ruptura ocorre a uma tensão menor que a
tensão de escoamento do material.
A fadiga é responsável por grande parte das falhas de
elementos mecânicos submetidos a carregamentos cíclicos.
60

61. Fluência e fadiga
Em projetos de elementos submetidos a carregamentos cíclicos utiliza-se o limite de resistência
a fadiga, que é a maior tensão aplicada sem a observação de evidências de falha nos elemento
testados.
Para a obtenção do limite de resistência a fadiga, corpos de prova são submetidos a
determinada tensão cíclica até falharem. Os resultados são marcados em um gráfico
denominado diagrama S-N (diagrama tensão-ciclo)
61

62. 62

63. Carga Axial
63

64. 64

65. Deformação elástica de um elemento
submetido a carga axial
Exemplo (prob. 4.4.): O eixo de cobre (E = 126 GPa) está sujeito as cargas axiais mostradas.
Determine o deslocamento da extremidade A em relação a extremidade D.
–dAB = 20 mm; dBC = 25 mm; dCD = 12 mm
65

66. Deformação elástica de um elemento
submetido a carga axial
Exemplo (prob. 4.3.): a coluna de aço A-36 é usada
para suportar as cargas simétricas dos dois pisos de
um edifício. Determine as cargas P1 e P2 se A se
mover 3 mm para baixo e B se mover 2,25 mm para
baixo quando as cargas forem aplicadas. Área
transversal do pilar: 14625 mm²
66

67. Exercício Avaliativo
A barra de aço A-36 mostrada na Figura 4.6a é composta por dois
segmentos, AB e BD, com áreas de seção transversal 600 mm2 e A
1.200 mm2, respectivamente. Determine o deslocamento vertical da
extremidade A e o deslocamento de B em relação a C.
67

68. Torção
68

69. Deformação por torção de um eixo circular
Torque é um momento que tende a torcer um elemento em torno de seu eixo longitudinal.
–Efeitos do torque:
69

70. Deformação por torção de um eixo circular
Ângulo de torção: este ângulo de depende da posição em relação a seção de referência.
70

71. Deformação por torção de um eixo
circular
Isolando um elemento a uma distância longitudinal x da seção de referência e uma posição
radial ρ pode-se entender a deformação por cisalhamento que ocorre devido a torção.
71

72. Exemplo
A distribuição de tensão em um eixo maciço foi
representada em gráfico ao longo de três linhas
radiais arbitrárias, como mostra a Figura 5.10a.
Determine o torque interno resultante na seção.
72

73. O eixo mostrado na Figura 5.12a está apoiado em
dois mancais e sujeito a três torques. Determine a
tensão de cisalhamento desenvolvida nos pontos
A e B localizados na seção a-a do eixo (Figura
5.12c).
73

74. 74

75. Transmissão de potência
Potencia é torque multiplicado pela velocidade angular do eixo;
75

76. Um eixo maciço de aço AB mostrado na
Figura 5.14 será utilizado para transmitir
3.750 W do motor M o qual está acoplado.
Se o eixo girar a w = 175 rpm e o aço tiver
uma tensão cisalhamento admissível de
100 MPa determine o diâmetro exigido
para o eixo com precisão de mm.
76

77. Um tubo de aço com diâmetro externo de 62,5 mm
é usado para transmitir 3 kW quando gira a 27
rev/minuto. Determine, com aproximação de
múltiplos de 5 mm, o diâmetro interno do tubo se a
tensão de cisalhamento admissível for Tadm = 70
MPa.
77

78. O projeto prevê que o eixo de transmissão AB será um tubo de
parede fina. O motor transmite 125 kW quando o eixo está
girando a 1500 rpm. Determine a espessura mínima da parede
do eixo se o diâmetro externo for de 62,5 mm e a tensão
admissível for de 50 MPa.
78

79. Equipamentos estáticos
CIARA BARCELOS
79