Estudo dos Triângulos e suas Propriedades O triângulo é uma figura geométrica plana formada por três lados, três ângulos e três vértices. Ele é considerado um dos polígonos mais importantes da Geometria, servindo de base para vários estudos matemáticos e aplicações práticas no cotidiano, como construções, engenharia, navegação, arquitetura e até mesmo em artes visuais. 🔹 Classificação dos Triângulos Os triângulos podem ser classificados de acordo com os lados ou com os ângulos: Quanto aos lados: Equilátero: possui os três lados iguais e, consequentemente, os três ângulos internos medem 60°. Isósceles: tem dois lados iguais e, por isso, os ângulos opostos a esses lados também são iguais. Escaleno: apresenta todos os lados diferentes, assim como os ângulos. 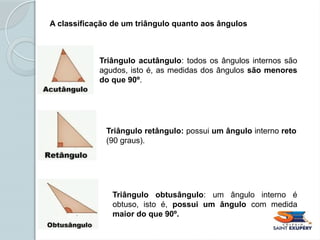Quanto aos ângulos: Acutângulo: todos os ângulos são menores que 90°. Retângulo: possui um ângulo reto (90°). Os lados que formam o ângulo reto são chamados de catetos, e o lado oposto é a hipotenusa. Obtusângulo: apresenta um ângulo maior que 90°. 🔹 Propriedades Fundamentais Soma dos ângulos internos A soma dos ângulos internos de qualquer triângulo é sempre igual a 180°. Desigualdade triangular Em qualquer triângulo, a soma das medidas de dois lados deve ser sempre maior que a medida do terceiro lado. Essa propriedade garante a existência do triângulo. Altura, mediana e bissetriz Altura: segmento que parte de um vértice e forma um ângulo reto com o lado oposto. Mediana: segmento que parte de um vértice e encontra o ponto médio do lado oposto. Bissetriz: segmento que divide um ângulo em duas partes iguais. Esses elementos internos são usados para calcular áreas, equilíbrios e pontos notáveis do triângulo. Área do triângulo A área pode ser determinada de diversas formas: Pela fórmula básica: 𝐴 = 𝑏 ⋅ ℎ 2 A= 2 b⋅h ​ , onde 𝑏 b é a base e ℎ h a altura. Pelo Teorema de Herão, quando conhecemos os três lados. 🔹 Triângulos Notáveis Triângulo equilátero: além de todos os lados iguais, possui simetria especial, sendo muito usado em cálculos geométricos. Triângulo retângulo: é de extrema importância porque nele se aplica o Teorema de Pitágoras, que estabelece a relação: 𝑎 2 = 𝑏 2 + 𝑐 2 a 2 =b 2 +c 2 onde 𝑎 a é a hipotenusa e 𝑏 , 𝑐 b,c são os catetos. 🔹 Pontos Notáveis No estudo dos triângulos, existem pontos especiais que surgem da interseção de elementos internos: Ortocentro: encontro das alturas. Baricentro: encontro das medianas, representando o centro de massa do triângulo. Circuncentro: encontro das mediatrizes, centro da circunferência que passa pelos vértices. Incentro: encontro das bissetrizes, centro da circunferência inscrita no triângulo. 🔹 Importância dos Triângulos Os triângulos são fundamentais não apenas no campo da Matemática, mas em diversas áreas práticas: Engenharia e Arquitetura: estruturas triangulares são usadas pela estabilidade que oferecem. Navegação e Astronomia: triângulos ajudam a calcular distâncias e posições. Tecnolo

1. Classificação dos Triângulos segundo o comprimento de seus
lados
 Módulos 46,47,48 e 49
O triângulo isósceles Caracterizado por ter dois
lados com a mesma medida, chamados de
congruentes.
No triângulo escaleno, os três lados possuem
medidas diferentes umas das outras e,
consequentemente, os ângulos são diferentes entre si.
O triângulo equilátero cujos lados são todos
congruentes, ou seja, têm a mesma medida. Com
isso, os três ângulos também são iguais e medem
60 graus.

2. A classificação de um triângulo quanto aos ângulos
Triângulo acutângulo: todos os ângulos internos são
agudos, isto é, as medidas dos ângulos são menores
do que 90º.
Triângulo obtusângulo: um ângulo interno é
obtuso, isto é, possui um ângulo com medida
maior do que 90º.
Triângulo retângulo: possui um ângulo interno reto
(90 graus).

3. Triângulos e Propriedades
 Vértices A,B e C
 Lados AB, BC, CA
 Ângulos internos a, b, c
 Ângulos externos e, f, g
A SOMA DAS MEDIDAS DOS ÂNGULOS INTERNOS É
IGUAL A 180°
Propriedade 1

4. Exemplo:
Ao traçar dois ângulos de medidas 40° e 67° partindo
respectivamente dos vértices A e B, um terceiro ângulo é
formado no ponto C, formando o triângulo ABC, como mostra a
figura.
X + 40° + 67° = 180°
X+ 107° = 180°
x= 180° - 107°
X= 73°
40°+ 67°+ 73° =180°

5. Propriedade 2
Em todo triângulo, os ângulos interno e externo, num mesmo
vértice, são adjacentes suplementares. Lembre-se de que
ângulos adjacentes são aqueles com um lado em comum,
mas nenhum ponto interno em comum.
a + x = 180°
b + y = 180°
c + z = 180°

6. Propriedade 3
Em todo triângulo, a medida de um ângulo externo é sempre igual
à soma das medidas dos ângulos internos não adjacentes a ele.
 139° é a soma dos ângulos internos não adjacentes a ele
90° e 49°
 131 é a soma dos ângulos internos não adjacentes a ele
90° e 41°
 90° é a soma dos ângulos 49° e 41

7. Propriedade 4
Em todo triângulo, ao maior ângulo, opõe-se o maior lado, ou seja
se encontra no lado oposto.
90° > 60 > 30°
oposto oposto oposto
2 1
> >

8. Exemplos:
1. Qual deve ser a medida de x?
X+ 50° = 120°
X = 120° - 50
X= 70°

9. 2. Exemplo:
O triângulo a seguir possui dois ângulos internos medem 40° e
60°. Quanto deve medir o ângulo externo não adjacente a
eles?
X = 60° + 40°
X= 100°
?

10. Exemplo 3:
x + x + 50° + 10° = 180°
2 x = 180° - 50° - 10°
2x = 120°
X = 120° = 60°
2
Os ângulos internos de um triângulo têm suas medidas
representadas°. Quanto mede cada ângulo desse triângulo?
60° + 50° = 110°
X = 60°