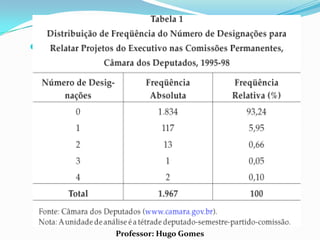
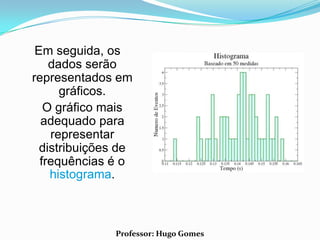
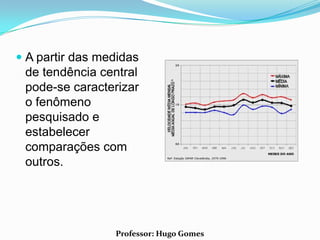
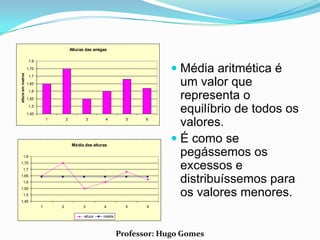
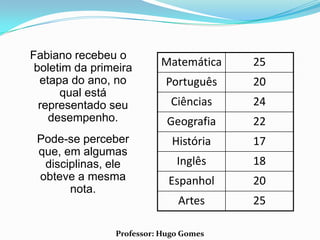
O documento discute conceitos estatísticos básicos como representações gráficas, medidas de tendência central e medidas de dispersão. As medidas de tendência central abordadas são média aritmética, moda e mediana. A moda é definida como o valor que mais se repete na série, enquanto a mediana separa os dados em duas metades iguais.