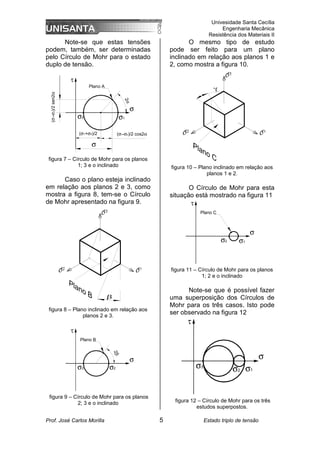
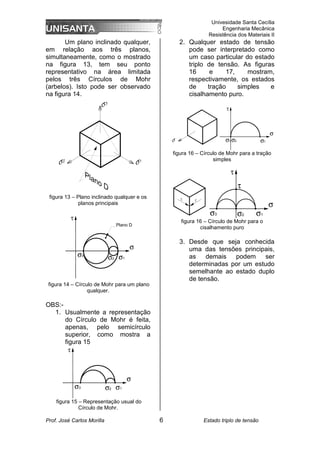
(1) O documento discute o estado triplo de tensão em um ponto, com tensões atuando em três direções ortogonais.
(2) É possível determinar as tensões principais, que são as tensões normais nos planos onde as tensões de cisalhamento são nulas.
(3) As tensões principais formam um elipsóide de tensões, onde a maior tensão principal é o valor máximo de tensão possível no ponto.