O documento apresenta uma análise de tensões em um elemento plano submetido a um estado plano de tensões. São determinadas: 1) As tensões normais e de cisalhamento no elemento após uma rotação de 30°; 2) As tensões principais e a tensão de cisalhamento máxima por meio do Círculo de Mohr; 3) Que os planos de tensão principal formam ângulos de 45° com os planos de tensão de cisalhamento máxima.

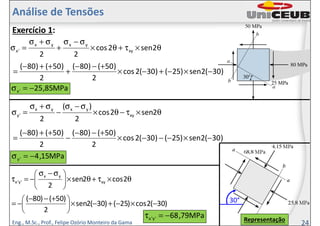
1. Eng., M.Sc., Prof., Felipe Ozório Monteiro da Gama
Exercício 1:
θ×τ+θ×
σ−σ
+
σ+σ
=σ 2sen2cos
22
xy
yxyx
'x
θ×τ+θ×




 σ−σ
−=τ 2cos2sen
2
xy
yx
'y'x
θ×τ−θ×
σ−σ
−
σ+σ
=σ 2sen2cos
2
)(
2
xy
yxyx
'y
Análise de Tensões
)30(2sen)25()30(2cos
2
)50()80(
2
)50()80(
−×−+−×
+−−
+
++−
=
MPa85,25'x −=σ
)30(2sen)25()30(2cos
2
)50()80(
2
)50()80(
−×−−−×
+−−
−
++−
=
MPa15,4'y −=σ
)30(2cos)25()30(2sen
2
)50()80(
−×−+−×




 +−−
−=
MPa79,68'y'x −=τ
24
30°
Representação

2. Eng., M.Sc., Prof., Felipe Ozório Monteiro da Gama
Confere!!!
Exercício 1:
Análise de Tensões
De fato, a soma das tensões normais em um elemento submetido ao ESTADO
PLANO DE TENSÕES independe da orientação desse elemento.
Concluímos que:
Verificando: 'y'xyx σ+σ=σ+σ
25
Para:
Tensões iniciais (σ)
(θ=0°)
MPa25
MPa50
MPa80
xy
y
x
−=τ
+=σ
−=σ
MPa8,68
MPa15,4
MPa84,25
'y'x
'y
'x
−=τ
−=σ
−=σ
Tensões transformadas (σ’)
(θ=30°)
)15,4(84,25 −+−5080 +− =
MPa30− MPa30−=

4. Eng., M.Sc., Prof., Felipe Ozório Monteiro da Gama
Tensões principais e Tensão de Cisalhamento Máxima
Na prática da engenharia é importante determinar a orientação dos planos em
que a tensão normal chega ao máximo e ao mínimo, assim como o plano no
qual a tensão de cisalhamento é máxima.
Tensões Principais
27

5. Eng., M.Sc., Prof., Felipe Ozório Monteiro da Gama
As equações de σx’ e τx’y’ são equações paramétricas de uma circunferência.
θτ+θ




 σ−σ
−=τ 2cos.2sen.
2
xy
yx
'y'x
( )2
( )2
+
Tensões principais e Tensão de Cisalhamento Máxima
Mudando essa parcela de membro.
θτ+θ
σ−σ
+
σ+σ
=σ 2sen.2cos.
22
xy
yxyx
'x
Depois, elevando-se ambas ao quadrado e somando, temos:
Temos:
2
xy
2
yx2
'y'x
2
yx
'x
22
τ+




 σ−σ
=τ+




 σ+σ
−σ Equação do
Círculo de Mohr
28
Tensões Principais

6. Eng., M.Sc., Prof., Felipe Ozório Monteiro da Gama
Substituindo na eq. acima:
2
yx
med
σσ
σ
+
=
2
2
2
xy
yx
R τ
σσ
+




 −
=
Então temos:
Que é a equação de uma
circunferência de raio R, com centro
no ponto C de abscissa σmed e
ordenada zero (0).
e
Tensões principais e Tensão de Cisalhamento Máxima
2
2
2
''
2
'
22
xy
yx
yx
yx
x τ
σσ
τ
σσ
σ +




 −
=+




 +
− Equação do
Círculo de Mohr
( ) 22
''
2
' Ryxmedx =+− τσσ
30
P=(x;y)
y
0x
Tensões Principais
σmed
a b=0

7. Eng., M.Sc., Prof., Felipe Ozório Monteiro da Gama
Essa equação define dois
valores 2θσ (θ e θ+180)
com diferença de 180° (A e
B) OU dois valores de 2θσ
(θ e θ+90) com diferença
de 90° (A e B).
Tensões principais (σ1 e σ2)
31
Determinação da direção que maximiza ou minimiza a tensão σx.
0
d
d 'x
=
θ
σ
∴
σ−σ
τ
=
θ
θ
∴
)(
2
2cos
2sen
yx
xy
2
2tg
yx
xy
σ−σ
τ
=θσ
θτ+θ
σ−σ
+
σ+σ
=σ 2sen.2cos.
22
xy
yxyx
'x
0
( ) θτ+θ
σ−σ
×−= 2cos22sen
2
2 xy
yx
-2 sen2θ 2 cos2θ
2
2tg
d
d
yx
xy'x
σ−σ
τ
=θ=
θ
σ
σ
1
1 = C + R
2
2 = C - R
2 = min
1 = max
θσ (elemento) = 2θσ (círculo)
Tensões Principais
R =
B (-σy;-τxy)
C
B (-σy;+τxy)
180º
90º
A (+σx;+τxy)
(θσ)
θσ = θp1 = Orientação (ângulo giro) do
elemento plano onde σx = σ1 e σy = σ2.

8. Eng., M.Sc., Prof., Felipe Ozório Monteiro da Gama
Desta forma, quando a orientação θ é tal que o plano dos pontos A e B,
coincidam com o plano das tensões principais, de forma que: σx = σ1 e σy = σ2, a
tensão cisalhante será nula!
Tensões principais (σ1 e σ2)
34
180º
B (-σy;0)
2 = min
A (+σx;0)
C
=0 =0
1 = max
0)'(
RC
RC
'y'x
mín2
máx1
=θτ
−=σ=σ
+=σ=σ
σ
Assim, as tensões cisalhantes atuantes nos planos de tensão normal principal
(máximas/mínimas), são sempre nulas!
2
xy
2
yxyx
mín,máx
22
τ+




 σ−σ
±
σ+σ
=σ
C = σmed
Raio
Tensões Principais
θσ (elemento) = 2θσ (círculo)Lembrando que:

9. Eng., M.Sc., Prof., Felipe Ozório Monteiro da Gama
θτ+θ




 σ−σ
−=τ 2cos.2sen.
2
xy
yx
'y'x
Essa equação define dois
valores 2θτ (θ e θ+180)
com diferença de 180° (A e
B) OU dois valores de 2θτ
(θ e θ+90) com diferença
de 90° (A e B).
Tensão de Cisalhamento Máxima (τmax)
35
Determinação da direção que maximiza a tensão τxy.
0
d
d 'y'x
=
θ
τ
∴
τ
σ−σ−
=
θ
θ
∴
xy
yx
2
)(
2cos
2sen
xy
yx
2
)(
2tg
τ
σ−σ−
=θτ
( ) θτ−θ
σ−σ
×−= 2sen22cos
2
2 xy
yx
2 cos2θ -2 sen2θ
xy
yx
'y'x 2
2tg
d
d
τ





 σ−σ
−
=θ=
θ
τ
τ
min
max = +Rmax
min = -R
Tensões Principais
θτ = θS1 = Orientação (ângulo giro)
do elemento plano onde τxy = τmax.
θσ (elemento) = 2θσ (círculo)
A (-σx;+τxy)
C
B (-σy;-τxy)
180º
90º
B (+σy;-τxy)
R
(θτ)

10. Eng., M.Sc., Prof., Felipe Ozório Monteiro da Gama
Desta forma, verifica-se que o máximo valor da tensão de cisalhamento é igual
ao raio R da circunferência.
36
As tensões normais atuantes nos planos de
tensão cisalhante máxima, são iguais à
média (σmed = C) das componentes de
tensão normal para θ = 0.
Tensão de Cisalhamento Máxima (τmax e τmin)
Tensões Principais
2
xy
2
yx
min,máx
2
R τ+




 σ−σ
±=±=τ ( )
2
' yx
méd'y'x
σ+σ
=σ=σ=θσ τ
C = σmed

11. Eng., M.Sc., Prof., Felipe Ozório Monteiro da Gama
=>
Como a tg 2θτ é o inverso negativo da tg 2θσ, os ângulos 2θτ e 2θσ tem
diferença de 90° e, portanto, os ângulos θτ e θσ são separados de 45°. Os
planos de máxima tensão de cisalhamento formam ângulo de 45° com os
planos principais.
37
Tensões Principais e Tensão de Cisalhamento Máxima
Tensões Principais
2
2tg
yx
xy
σ−σ
τ
=θσ
xy
yx
2
)(
2tg
τ
σ−σ−
=θτ
θ(elemento) = 2θ(círculo)
INVERSO
NEGATIVO
x’
θσ
x’
σmed
45°
θτ
θτ
=>
θσ = θτ - 45º

12. Eng., M.Sc., Prof., Felipe Ozório Monteiro da Gama
Tensões principais: Planos principais:
Tensão de cisalhamento máxima:
39
Tensões Principais e Tensão de Cisalhamento Máxima





 σ−σ
τ
=θσ
2
2tg
yx
xy
xy
yx
2
2tg
τ





 σ−σ
−
=θτ
RC
RC
mín2
máx1
−=σ=σ
+=σ=σ
2
xy
2
yxyx
mín,máx
22
τ+




 σ−σ
±
σ+σ
=σ
C = σmed
Raio
2
xy
2
yx
min,máx
2
R τ+




 σ−σ
±=±=τ
( )
2
' yx
méd'y'x
σ+σ
=σ=σ=θσ τ
C = σmed
Planos principais:
θσ (elemento) = 2θσ (círculo)
( ) 0''y'x =θτ σ
Tensões Principais
θσ = θτ - 45º