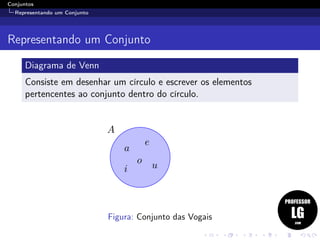
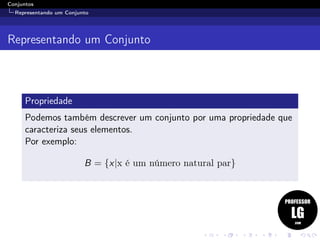
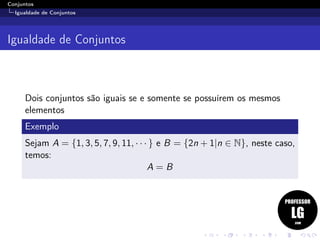
1. O documento discute os conceitos básicos de conjuntos, incluindo definições de conjunto, elemento, pertinência e representações de conjuntos através de diagramas de Venn, enumeração e propriedades. 2. A igualdade de conjuntos é explicada como sendo quando dois conjuntos possuem exatamente os mesmos elementos, independente da ordem ou repetição. 3. Conjuntos vazios, unitários e universos são definidos, sendo o conjunto vazio aquele sem elementos, o unitário com um único elemento e o universo contendo todos os

1. Conjuntos
Conjuntos
Professor LG
2017

2. Conjuntos
1 Conjunto - Elemento - Pertinência
2 Representando um Conjunto
3 Igualdade de Conjuntos
4 Conjuntos Vazio, Unitário e Universo

3. Conjuntos
Conjunto - Elemento - Pertinência
Conjunto - Elemento - Pertinência
Noções Primitivas
No estudo de conjuntos três noções são aceitas sem definição:
Conjunto
Elemento
Pertinência

4. Conjuntos
Conjunto - Elemento - Pertinência
Conjunto - Elemento - Pertinência
Intuitivamente, conjunto é uma lista ou coleção bem definida de
objetos.
São exemplos de conjuntos:
1 Conjunto das vogais
2 Conjunto dos números naturais pares
3 Conjunto das estações do ano

5. Conjuntos
Conjunto - Elemento - Pertinência
Conjunto - Elemento - Pertinência
Intuitivamente, conjunto é uma lista ou coleção bem definida de
objetos.
São exemplos de conjuntos:
1 Conjunto das vogais
2 Conjunto dos números naturais pares
3 Conjunto das estações do ano
Cada um dos membros que formam um conjunto é denominado de
elemento. Os conjuntos acima possuem os seguintes elementos:
1 a, e, i, o, u
2 0, 2, 4, 6, 8, 10, · · ·
3 Primavera, Verão, Outono, Inverno

6. Conjuntos
Conjunto - Elemento - Pertinência
Conjunto - Elemento - Pertinência
Em geral indicamos conjuntos com letras maiúsculas
(A, B, C, D, · · · ) e elementos com letras minúsculas (a, b, c, d, · · · ).
Relação de Pertinência
Seja A um conjunto e a um elemento.
Se a pertence ao conjunto A, escrevemos:
a ∈ A
Caso a não seja um elemento de A, escrevemos:
a ∈ A

7. Conjuntos
Representando um Conjunto
Representando um Conjunto
As principais formas de representação de um conjunto são:
Diagrama de Venn
Enumeração
Propriedade

8. Conjuntos
Representando um Conjunto
Representando um Conjunto
Diagrama de Venn
Consiste em desenhar um círculo e escrever os elementos
pertencentes ao conjunto dentro do círculo.
Figura: Conjunto das Vogais

9. Conjuntos
Representando um Conjunto
Representando um Conjunto
Enumeração
Basta indicar os elementos do conjunto entre chaves.
Exemplos:
A = {a, e, i, o, u}
B = {0, 2, 4, 6, 8, 10, · · · }
C = {Primavera, Verão, Outono, Inverno}

10. Conjuntos
Representando um Conjunto
Representando um Conjunto
Propriedade
Podemos também descrever um conjunto por uma propriedade que
caracteriza seus elementos.
Por exemplo:
B = {x|x é um número natural par}

11. Conjuntos
Igualdade de Conjuntos
Igualdade de Conjuntos
Dois conjuntos são iguais se e somente se possuírem os mesmos
elementos
Exemplo
Sejam A = {1, 3, 5, 7, 9, 11, · · · } e B = {2n + 1|n ∈ N}, neste caso,
temos:
A = B

12. Conjuntos
Igualdade de Conjuntos
Igualdade de Conjuntos
Observações
Elementos repetidos, por simplicidade, podem ser considerados
uma única vez.
{1, 2, 2, 3, 3, 3, 4, 4, 4, 4} = {1, 2, 3, 4}
A ordem dos elementos não importa.
{a, e, i, o, u} = {u, o, i, e, a}
Quando o conjunto A não é igual ao conjunto B, escrevemos:
A = B

13. Conjuntos
Conjuntos Vazio, Unitário e Universo
Conjuntos Vazio, Unitário e Universo
Conjunto Vazio
Denominamos de conjunto vazio, cuja notação é ∅, o conjunto que
não possui elementos.
Podemos usar uma propriedade contraditória para definir o
conjunto vazio, por exemplo:
∅ = {x|x = x}
Outra maneira de representar o conjunto vazio é através de duas
chaves:
∅ = {}

14. Conjuntos
Conjuntos Vazio, Unitário e Universo
Conjuntos Vazio, Unitário e Universo
Conjunto Unitário
Se um conjunto possui apenas um elemento, ele é denominado de
conjunto unitário.
Exemplo:
A = {x ∈ N|x é um número par e primo}
Observe que o conjunto {∅} = ∅ uma vez que, {∅} é um conjunto
unitário, sendo o conjunto vazio seu único elemento.

15. Conjuntos
Conjuntos Vazio, Unitário e Universo
Conjuntos Vazio, Unitário e Universo
Conjunto Universo
O conjunto que possui todos os elementos relativos a um
determinado assunto com o qual estamos trabalhando é chamado
de conjunto universo e o denotamos por U.

16. Conjuntos
Conjuntos Vazio, Unitário e Universo
Quando resolvemos uma equação é importante termos o conjunto
universo bem definido, conforme podemos ver na tabela abaixo:
Universo N Z Q R
x2 = 2 ∅ ∅ ∅ −
√
2,
√
2
5x = 3 ∅ ∅
3
5
3
5
x + 9 = 4 ∅ {−5} {−5} {−5}
x + 7 = 10 {3} {3} {3} {3}