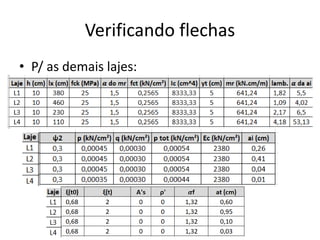
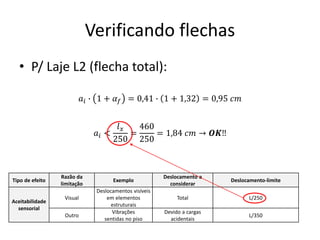
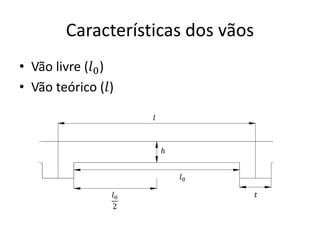
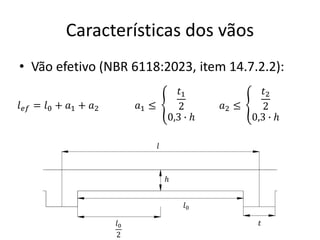
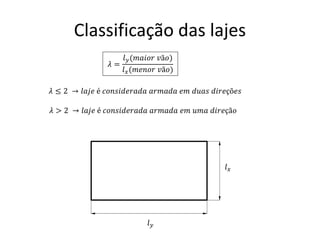
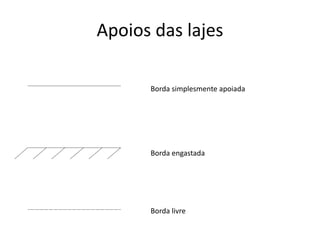
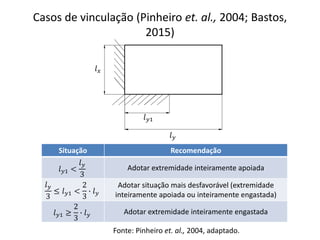
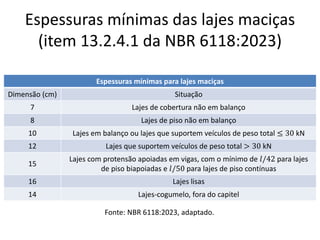
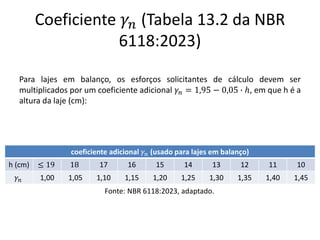
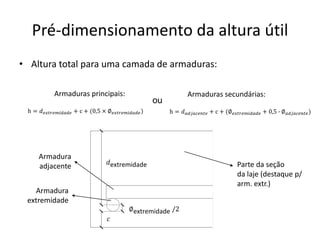
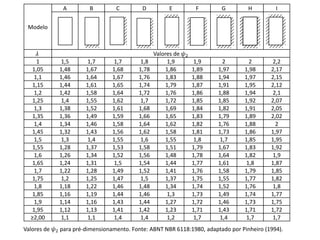
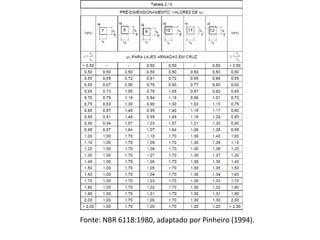
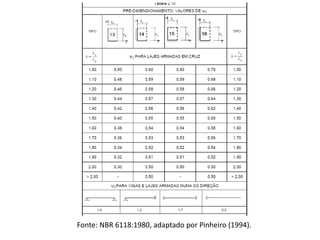
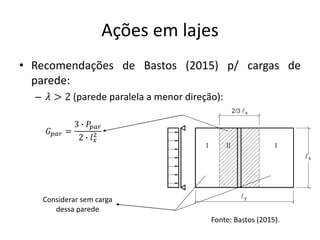
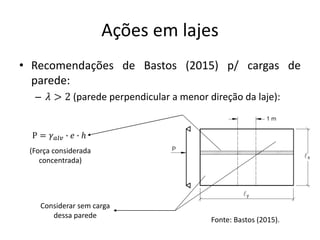
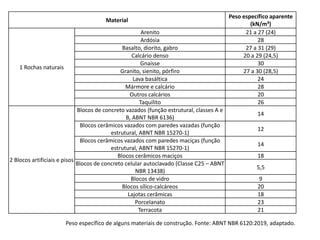
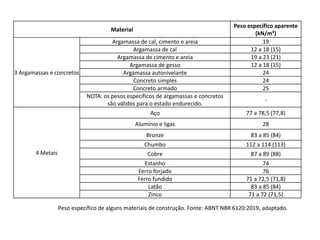
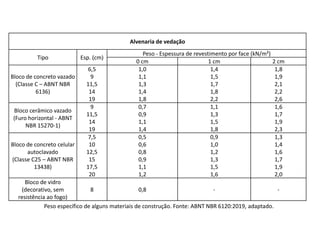
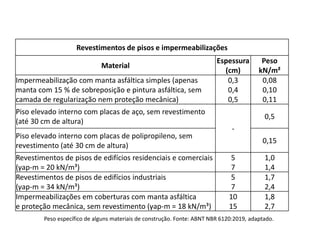
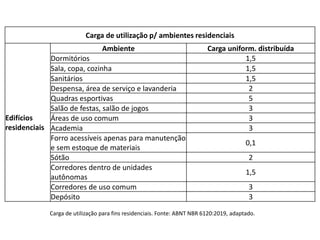
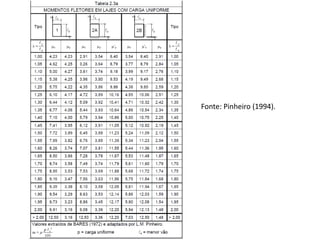
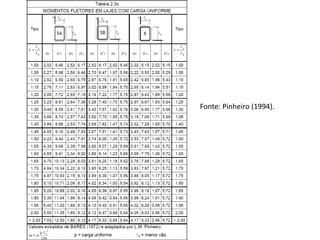
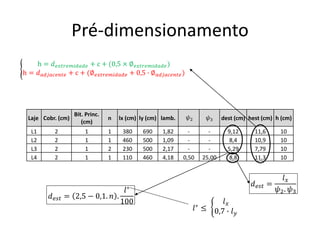
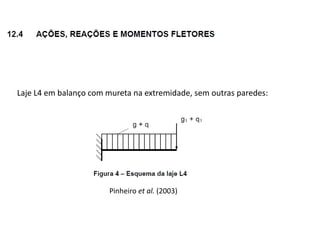
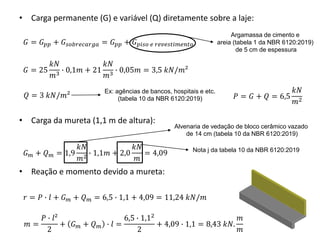
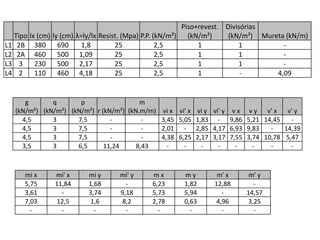
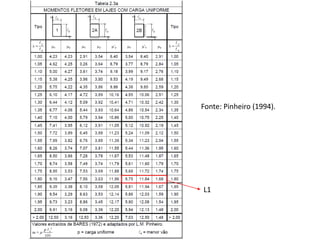
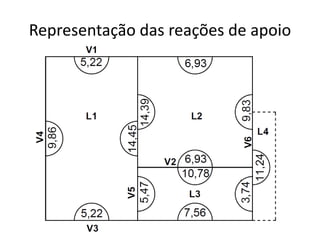
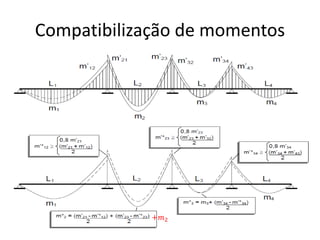
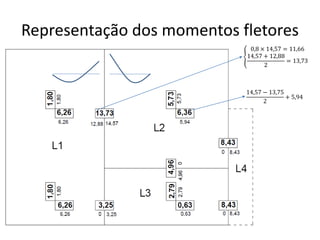
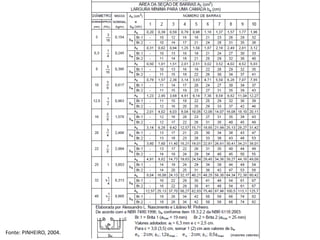
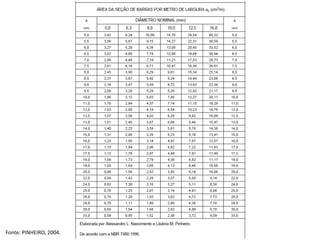
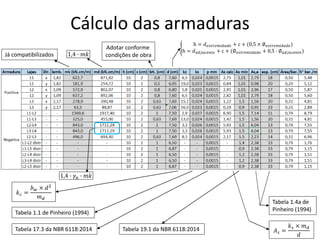
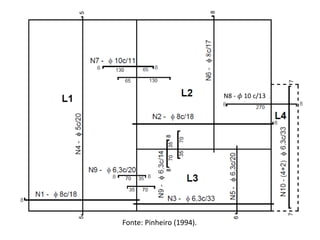
O documento aborda lajes maciças, definindo suas características, carregamentos e classificação segundo normativas como a NBR 6118:2023. Inclui detalhes sobre espessura mínima, coeficiente de solicitação e pré-dimensionamento, além de considerar as ações das cargas em lajes. Também cita pesos específicos de materiais de construção e recomendações sobre apoios e vinculações.

1. Lajes Maciças
Prof. Pedro Paulo Martins de
Carvalho

2. Introdução
• Definição
• Função
• Carregamentos
Disponível em:
https://www.facebook.com/engenhariacasaconstrucao/photos/a.5624
29744181450/595666130857811/?type=3

3. Características dos vãos
• Vão livre (𝑙0)
• Vão teórico (𝑙)
𝑙0
2
𝑙0
ℎ
𝑙
𝑡

4. Características dos vãos
• Vão efetivo (NBR 6118:2023, item 14.7.2.2):
𝑙0
2
𝑙0
ℎ
𝑙
𝑡
𝑙𝑒𝑓 = 𝑙0 + 𝑎1 + 𝑎2 𝑎1 ≤ 𝑎2 ≤
ቐ
𝑡1
2
0,3 ∙ ℎ
ቐ
𝑡2
2
0,3 ∙ ℎ

5. Classificação das lajes
𝜆 =
𝑙𝑦(𝑚𝑎𝑖𝑜𝑟 𝑣ã𝑜)
𝑙𝑥(𝑚𝑒𝑛𝑜𝑟 𝑣ã𝑜)
𝜆 ≤ 2 → 𝑙𝑎𝑗𝑒 é 𝑐𝑜𝑛𝑠𝑖𝑑𝑒𝑟𝑎𝑑𝑎 𝑎𝑟𝑚𝑎𝑑𝑎 𝑒𝑚 𝑑𝑢𝑎𝑠 𝑑𝑖𝑟𝑒çõ𝑒𝑠
𝜆 > 2 → 𝑙𝑎𝑗𝑒 é 𝑐𝑜𝑛𝑠𝑖𝑑𝑒𝑟𝑎𝑑𝑎 𝑎𝑟𝑚𝑎𝑑𝑎 𝑒𝑚 𝑢𝑚𝑎 𝑑𝑖𝑟𝑒çã𝑜
𝑙𝑦
𝑙𝑥

6. Apoios das lajes
• No encontro de lajes adjacentes (momento
negativo), deve-se verificar a diferença de
porte, momento fletor e a espessura dessas
lajes para então considerar o tipo de vínculo.

7. Apoios das lajes
Borda simplesmente apoiada
Borda engastada
Borda livre

8. Casos de vinculação (Pinheiro et. al., 2004; Bastos,
2015)
𝑙𝑦
𝑙𝑦1
𝑙𝑥
Situação Recomendação
𝑙𝑦1 <
𝑙𝑦
3
Adotar extremidade inteiramente apoiada
𝑙𝑦
3
≤ 𝑙𝑦1 <
2
3
∙ 𝑙𝑦
Adotar situação mais desfavorável (extremidade
inteiramente apoiada ou inteiramente engastada)
𝑙𝑦1 ≥
2
3
∙ 𝑙𝑦 Adotar extremidade inteiramente engastada
Fonte: Pinheiro et. al., 2004, adaptado.

9. Espessuras mínimas das lajes maciças
(item 13.2.4.1 da NBR 6118:2023)
Espessuras mínimas para lajes maciças
Dimensão (cm) Situação
7 Lajes de cobertura não em balanço
8 Lajes de piso não em balanço
10 Lajes em balanço ou lajes que suportem veículos de peso total ≤ 30 kN
12 Lajes que suportem veículos de peso total > 30 kN
15
Lajes com protensão apoiadas em vigas, com o mínimo de 𝑙/42 para lajes
de piso biapoiadas e 𝑙/50 para lajes de piso contínuas
16 Lajes lisas
14 Lajes-cogumelo, fora do capitel
Fonte: NBR 6118:2023, adaptado.

10. Coeficiente 𝛾𝑛 (Tabela 13.2 da NBR
6118:2023)
Para lajes em balanço, os esforços solicitantes de cálculo devem ser
multiplicados por um coeficiente adicional 𝛾𝑛 = 1,95 − 0,05 ∙ ℎ, em que h é a
altura da laje (cm):
coeficiente adicional 𝛾𝑛 (usado para lajes em balanço)
h (cm) ≤ 19 18 17 16 15 14 13 12 11 10
𝛾𝑛 1,00 1,05 1,10 1,15 1,20 1,25 1,30 1,35 1,40 1,45
Fonte: NBR 6118:2023, adaptado.

11. Cobrimentos (tabela 7.2 da NBR
6118:2023)
Cobrimento nominal para cada classe de agressividade, para ∆𝒄 = 𝟏𝟎 𝒎𝒎
Tipo de elemento
Classe de agressividade ambiental
I II III IV¹
Cobrimento nominal (mm)
Laje² (concreto armado) 20 25 35 45
¹Nas superfícies expostas a ambientes agressivos, como reservatórios, estações de tratamento de água
e esgoto, condutos de esgoto, canaletas de efluentes e outras obras em ambientes química e
intensamente agressivos, devem ser atendidos os cobrimentos da classe de agressividade IV.
²Para a face superior de lajes e vigas que serão revestidas com argamassa de contrapiso, com
revestimentos finais secos tipo carpete e madeira, com argamassa de revestimento e acabamento,
como pisos de elevado desempenho, pisos cerâmicos, pisos asfálticos e outros, as exigências desta
Tabela podem ser substituídas pelas de 7.4.7.5, respeitado um cobrimento nominal ≥ 15 mm.
Fonte: NBR 6118:2023, adaptado.

12. Pré-dimensionamento da altura útil
• Não consta na NBR 6118:2023;
• Método utilizado tradicionalmente para lajes retangulares de
extremidades apoiadas ou engastadas (Pinheiro et. al., 2004 e
Bastos, 2015):
– d é a altura útil da laje (cm)
– 𝑛 corresponde ao número de bordas engastadas
– 𝑙∗
(m) é o menor entre:
𝑑 =
2,5 − 0,1 ∙ 𝑛 ∙ 𝑙∗
100
ቊ
𝑙𝑥
0,7 ∙ 𝑙𝑦

13. Pré-dimensionamento da altura útil
• Altura total para uma camada de armaduras:
ou
h = 𝑑𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡𝑒 + c + (∅𝑒𝑥𝑡𝑟𝑒𝑚𝑖𝑑𝑎𝑑𝑒 + 0,5 ∙ ∅𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡𝑒)
h = 𝑑𝑒𝑥𝑡𝑟𝑒𝑚𝑖𝑑𝑎𝑑𝑒 + c + (0,5 × ∅𝑒𝑥𝑡𝑟𝑒𝑚𝑖𝑑𝑎𝑑𝑒)
Armaduras principais: Armaduras secundárias:
∅extremidade /2
𝑑extremidade Parte da seção
da laje (destaque p/
arm. extr.)
𝑐
Armadura
extremidade
Armadura
adjacente

14. Pré-dimensionamento da altura útil
• Armadura principal:
– As negativas mais próximas às extremidades da seção
– Todas as positivas, quando 𝜆 ≤ 2
– Apenas as paralelas ao menor vão, quando 𝜆 > 2
• Armadura secundárias:
– Demais situações

15. Pré-dimensionamento da altura útil
• Método que era recomendado pela ABNT NBR 6118:1980, item
4.2.3.1 C:
– d é a altura útil da laje (cm)
– 𝑙𝑥 é o menor vão
– 𝜓2 é o coeficiente relacionado aos vínculos e dimensões da laje
– 𝜓3 é o coeficiente que depende do aço considerado
𝑑 ≥
𝑙𝑥
𝜓2 ∙ 𝜓3

16. Pré-dimensionamento da altura útil
𝜓3 para pré-dimensionamento
𝑓𝑦𝑘 do aço (MPa)
Vigas e lajes
nervuradas
Lajes maciças
250 25 35
500 17 25
600 15 20
Fonte: NBR 6118:1980, adaptado.

17. Modelo
A B C D E F G H I
𝜆 Valores de 𝜓2
1 1,5 1,7 1,7 1,8 1,9 1,9 2 2 2,2
1,05 1,48 1,67 1,68 1,78 1,86 1,89 1,97 1,98 2,17
1,1 1,46 1,64 1,67 1,76 1,83 1,88 1,94 1,97 2,15
1,15 1,44 1,61 1,65 1,74 1,79 1,87 1,91 1,95 2,12
1,2 1,42 1,58 1,64 1,72 1,76 1,86 1,88 1,94 2,1
1,25 1,4 1,55 1,62 1,7 1,72 1,85 1,85 1,92 2,07
1,3 1,38 1,52 1,61 1,68 1,69 1,84 1,82 1,91 2,05
1,35 1,36 1,49 1,59 1,66 1,65 1,83 1,79 1,89 2,02
1,4 1,34 1,46 1,58 1,64 1,62 1,82 1,76 1,88 2
1,45 1,32 1,43 1,56 1,62 1,58 1,81 1,73 1,86 1,97
1,5 1,3 1,4 1,55 1,6 1,55 1,8 1,7 1,85 1,95
1,55 1,28 1,37 1,53 1,58 1,51 1,79 1,67 1,83 1,92
1,6 1,26 1,34 1,52 1,56 1,48 1,78 1,64 1,82 1,9
1,65 1,24 1,31 1,5 1,54 1,44 1,77 1,61 1,8 1,87
1,7 1,22 1,28 1,49 1,52 1,41 1,76 1,58 1,79 1,85
1,75 1,2 1,25 1,47 1,5 1,37 1,75 1,55 1,77 1,82
1,8 1,18 1,22 1,46 1,48 1,34 1,74 1,52 1,76 1,8
1,85 1,16 1,19 1,44 1,46 1,3 1,73 1,49 1,74 1,77
1,9 1,14 1,16 1,43 1,44 1,27 1,72 1,46 1,73 1,75
1,95 1,12 1,13 1,41 1,42 1,23 1,71 1,43 1,71 1,72
≥2,00 1,1 1,1 1,4 1,4 1,2 1,7 1,4 1,7 1,7
Valores de 𝜓2 para pré-dimensionamento. Fonte: ABNT NBR 6118:1980, adaptado por Pinheiro (1994).

18. Fonte: NBR 6118:1980, adaptado por Pinheiro (1994).

19. Fonte: NBR 6118:1980, adaptado por Pinheiro (1994).

20. Ações em lajes
• São consideradas as seguintes cargas sobre as lajes:
– Peso próprio das lajes;
– Revestimentos;
– Piso e contrapiso;
– Paredes;
– Carga de utilização.
• Pinheiro et al. (2003) considera que as cargas de
paredes apoiadas diretamente na laje podem, em
geral, ser admitidas uniformemente distribuídas na
laje, recomendando carga maior ou igual a um terço da
carga da parede por metro linear ou 1 kN/m² em caso
de paredes em posição não definida.

21. Ações em lajes
• Recomendações de Bastos (2015) p/ cargas de
parede:
– 𝜆 ≤ 2:
𝐺𝑝𝑎𝑟𝑒𝑑𝑒 =
𝛾𝑎𝑙𝑣 ∙ 𝑒 ∙ ℎ ∙ 𝑙
𝐴
• 𝛾𝑎𝑙𝑣 - peso específico da unidade de alvenaria que compõe a
parede (kN/m3);
• 𝐺𝑝𝑎𝑟𝑒𝑑𝑒 - carga uniforme da parede (kN/m2);
• 𝑒 - espessura total da parede (m);
• ℎ - altura da parede (m);
• 𝑙 - comprimento da parede (m);
• 𝐴 - área da laje em planta (m2)
NBR 6120

22. Ações em lajes
• Recomendações de Bastos (2015) p/ cargas de
parede:
– 𝜆 ≤ 2 (considerando o revestimento):
𝛾𝑝𝑎𝑟 = 𝛾𝑎𝑙𝑣 ∙ 𝑒𝑎𝑙𝑣 + 𝛾𝑎𝑟𝑔 ∙ 𝑒𝑎𝑟𝑔
• 𝛾𝑝𝑎𝑟 - peso específico da parede (kN/m²3);
• 𝛾𝑎𝑙𝑣- peso específico da unidade de alvenaria (kN/m³2);
• 𝑒 - espessura da unidade de alvenaria (m);
• 𝛾𝑎𝑟𝑔 - peso específico da argamassa do revestimento (kN/m³3);
• 𝑒𝑎𝑟𝑔- espessura do revestimento (m).
𝐺𝑝𝑎𝑟 =
𝛾𝑝𝑎𝑟 ∙ ℎ ∙ 𝑙
𝐴

23. Ações em lajes
• Recomendações de Bastos (2015) p/ cargas de
parede:
– 𝜆 > 2 (parede paralela a menor direção):
𝐺𝑝𝑎𝑟 =
3 ∙ 𝑃𝑝𝑎𝑟
2 ∙ 𝑙𝑥
2
Considerar sem carga
dessa parede
Fonte: Bastos (2015).

24. Ações em lajes
• Recomendações de Bastos (2015) p/ cargas de
parede:
– 𝜆 > 2 (parede perpendicular a menor direção da laje):
P = 𝛾𝑎𝑙𝑣 ∙ 𝑒 ∙ ℎ
Considerar sem carga
dessa parede
(Força considerada
concentrada)
Fonte: Bastos (2015).

25. Peso específico de alguns materiais de construção. Fonte: ABNT NBR 6120:2019, adaptado.
Material
Peso específico aparente
(kN/m³)
1 Rochas naturais
Arenito 21 a 27 (24)
Ardósia 28
Basalto, diorito, gabro 27 a 31 (29)
Calcário denso 20 a 29 (24,5)
Gnaisse 30
Granito, sienito, pórfiro 27 a 30 (28,5)
Lava basáltica 24
Mármore e calcário 28
Outros calcários 20
Taquilito 26
2 Blocos artificiais e pisos
Blocos de concreto vazados (função estrutural, classes A e
B, ABNT NBR 6136)
14
Blocos cerâmicos vazados com paredes vazadas (função
estrutural, ABNT NBR 15270-1)
12
Blocos cerâmicos vazados com paredes maciças (função
estrutural, ABNT NBR 15270-1)
14
Blocos cerâmicos maciços 18
Blocos de concreto celular autoclavado (Classe C25 – ABNT
NBR 13438)
5,5
Blocos de vidro 9
Blocos sílico-calcáreos 20
Lajotas cerâmicas 18
Porcelanato 23
Terracota 21

26. Peso específico de alguns materiais de construção. Fonte: ABNT NBR 6120:2019, adaptado.
Material
Peso específico aparente
(kN/m³)
3 Argamassas e concretos
Argamassa de cal, cimento e areia 19
Argamassa de cal 12 a 18 (15)
Argamassa de cimento e areia 19 a 23 (21)
Argamassa de gesso 12 a 18 (15)
Argamassa autonivelante 24
Concreto simples 24
Concreto armado 25
NOTA: os pesos específicos de argamassas e concretos
são válidos para o estado endurecido.
-
4 Metais
Aço 77 a 78,5 (77,8)
Alumínio e ligas 28
Bronze 83 a 85 (84)
Chumbo 112 a 114 (113)
Cobre 87 a 89 (88)
Estanho 74
Ferro forjado 76
Ferro fundido 71 a 72,5 (71,8)
Latão 83 a 85 (84)
Zinco 71 a 72 (71,5)

27. Alvenaria de vedação
Tipo Esp. (cm)
Peso - Espessura de revestimento por face (kN/m²)
0 cm 1 cm 2 cm
Bloco de concreto vazado
(Classe C – ABNT NBR
6136)
6,5
9
11,5
14
19
1,0
1,1
1,3
1,4
1,8
1,4
1,5
1,7
1,8
2,2
1,8
1,9
2,1
2,2
2,6
Bloco cerâmico vazado
(Furo horizontal - ABNT
NBR 15270-1)
9
11,5
14
19
0,7
0,9
1,1
1,4
1,1
1,3
1,5
1,8
1,6
1,7
1,9
2,3
Bloco de concreto celular
autoclavado
(Classe C25 – ABNT NBR
13438)
7,5
10
12,5
15
17,5
20
0,5
0,6
0,8
0,9
1,1
1,2
0,9
1,0
1,2
1,3
1,5
1,6
1,3
1,4
1,6
1,7
1,9
2,0
Bloco de vidro
(decorativo, sem
resistência ao fogo)
8 0,8 - -
Peso específico de alguns materiais de construção. Fonte: ABNT NBR 6120:2019, adaptado.

28. Revestimentos de pisos e impermeabilizações
Material
Espessura
(cm)
Peso
kN/m²
Impermeabilização com manta asfáltica simples (apenas
manta com 15 % de sobreposição e pintura asfáltica, sem
camada de regularização nem proteção mecânica)
0,3
0,4
0,5
0,08
0,10
0,11
Piso elevado interno com placas de aço, sem revestimento
(até 30 cm de altura)
-
0,5
Piso elevado interno com placas de polipropileno, sem
revestimento (até 30 cm de altura)
0,15
Revestimentos de pisos de edifícios residenciais e comerciais
(γap-m = 20 kN/m³)
5
7
1,0
1,4
Revestimentos de pisos de edifícios industriais
(γap-m = 34 kN/m³)
5
7
1,7
2,4
Impermeabilizações em coberturas com manta asfáltica
e proteção mecânica, sem revestimento (γap-m = 18 kN/m³)
10
15
1,8
2,7
Peso específico de alguns materiais de construção. Fonte: ABNT NBR 6120:2019, adaptado.

29. Carga de utilização p/ ambientes residenciais
Edifícios
residenciais
Ambiente Carga uniform. distribuída
Dormitórios 1,5
Sala, copa, cozinha 1,5
Sanitários 1,5
Despensa, área de serviço e lavanderia 2
Quadras esportivas 5
Salão de festas, salão de jogos 3
Áreas de uso comum 3
Academia 3
Forro acessíveis apenas para manutenção
e sem estoque de materiais
0,1
Sótão 2
Corredores dentro de unidades
autônomas
1,5
Corredores de uso comum 3
Depósito 3
Carga de utilização para fins residenciais. Fonte: ABNT NBR 6120:2019, adaptado.

30. Ações em lajes
• Exemplo: calcular carga da parede (esp. nom. do
elem.: 14 cm; e revestimento por face: 2 cm) de 2,8
m de altura para a laje ilustrada a seguir:
𝐺𝑝𝑎𝑟 =
𝛾𝑝𝑎𝑟 ∙ ℎ ∙ 𝑙
𝐴
𝐺𝑝𝑎𝑟 =
1,9 ∙ 2,8 ∙ 4,39
4,5 ∙ 5,5
𝐺𝑝𝑎𝑟 = 0,95 𝑘𝑁/𝑚²

31. Cálculo das reações de apoio pelo
método das charneiras plásticas
• Charneiras aproximadas (item 14.7.6.1 – b):
– 45° entre dois apoios do mesmo tipo;
– 60° a partir do apoio considerado engastado, se o outro for
considerado simplesmente apoiado;
– 90° a partir do apoio, quando a borda vizinha for livre.
Fonte: Pinheiro (2003).

32. Cálculo das reações de apoio pelo
método das charneiras plásticas
• Cálculo por meio de tabelas (Pinheiro, 1994),
usando para 𝜐, coeficientes adimensionais
(𝜈𝑥, 𝜈𝑦, 𝜈′𝑥, 𝜈′𝑦), o que resulta nas reações de
apoio: 𝑣𝑥, 𝑣𝑦, 𝑣′𝑥, 𝑣′𝑦:
𝑣 = 𝜐 ∙
𝑝 ∙ 𝑙𝑥
10

33. Fonte: Pinheiro (1994).

34. Fonte: Pinheiro (1994).

35. Fonte: Pinheiro (1994).

36. Cálculo do momento fletor
• Método elástico:
– Baseado na teoria clássica de placas delgadas
(Teoria de Kirchhoff)

37. Cálculo do momento fletor
• Cálculo por meio de tabelas:
– Adota-se coeficiente de Poisson igual a 0,15.
– Adota-se coeficientes tabelados (Pinheiro, 1994):
𝜇𝑥, 𝜇𝑦, 𝜇′𝑥, 𝜇′𝑦 para calcular os momentos: 𝑚𝑥,
𝑚𝑦, 𝑚′𝑥, 𝑚′𝑦.
𝑚 = 𝜇 ∙
𝑝 ∙ 𝑙𝑥
2
10
𝑚𝑥, 𝑚′𝑥 - momentos na direção de 𝑙𝑥
𝑚𝑦, 𝑚′𝑦 - momentos na direção de 𝑙𝑦

38. Fonte: Pinheiro (1994).

39. Fonte: Pinheiro (1994).

40. Fonte: Pinheiro (1994).

41. Fonte: Pinheiro (1994).

42. Fonte: Pinheiro (1994).

43. Lajes de geometrias complexas
• Em lajes de geometrias complexas, os métodos numéricos
conduzem a resultados mais precisos;
• No entanto, alguns autores sugerem formas simplificadas de
determinação de esforços nesses casos, como admitir apoios
simples quando for adequado, conforme proposto por
Chamberlain (2001):
Momentos positivos:
𝑀𝑥 =
𝑝𝑑 ∙ 𝐿𝑥
2
8
𝑀𝑦 =
𝑝𝑑 ∙ 𝐿𝑦
2
8

44. Compatibilização de momentos
fletores em lajes
Prof. Pedro Paulo Martins de
Carvalho

45. Compatibilização de momentos em lajes
adjacentes (item 14.7.6.2 da NBR 6118:2014)
• Situação de predominância
de cargas permanentes:
considerar inicialmente
lajes isoladas e realizar
posterior compatibilização
simplificada;
• É permitido adotar maior
momento negativo ou
equilibrar os momentos.
Fonte: Pinheiro et. al., 2004

46. Fonte: Pinheiro et. al., 2004

47. Critério
• Momentos negativos diferentes advindos de
lajes adjacentes.
• P/ Momentos da mesma ordem de grandeza:
Caso a compatibilidade gere
tendência de aumento do
momento positivo, considerar!
Maior negativo
Menor negativo

48. +𝑚2
Fonte: Pinheiro et. al., 2004

49. Critério
• Se, por exemplo:
𝑚′12 < 0,5 𝑚′21 ,
podemos adotar L1
engastada e L2
simplesmente
apoiada nas bordas
de contato dessas
duas lajes.
Fonte: Pinheiro et. al., 2004

50. Exemplo de dimensionamento
(Pinheiro et al., 1994)

51. Exemplo de dimensionamento
• Classe de agressividade fraca;
• Concreto C25;
• Desconsiderar eventuais ações horizontais;
• Usar aço CA-50 e bitola da armadura principal: 10 mm;
• Para a estimativa da altura útil:
– Usar método tradicional para lajes com extremidades apoiadas ou
engastadas;
– Usar método da NBR 6118:1980 para lajes em balanço.

54. Pré-dimensionamento
𝑑𝑒𝑠𝑡 = 2,5 − 0,1. 𝑛 .
𝑙∗
100
൝
h = 𝑑𝑒𝑥𝑡𝑟𝑒𝑚𝑖𝑑𝑎𝑑𝑒 + c + (0,5 × ∅𝑒𝑥𝑡𝑟𝑒𝑚𝑖𝑑𝑎𝑑𝑒)
h = 𝑑𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡𝑒 + c + (∅𝑒𝑥𝑡𝑟𝑒𝑚𝑖𝑑𝑎𝑑𝑒 + 0,5 ∙ ∅𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡𝑒)
Laje Cobr. (cm)
Bit. Princ.
(cm)
n lx (cm) ly (cm) lamb. dest (cm) hest (cm) h (cm)
L1 2 1 1 380 690 1,82 - - 9,12 11,6 10
L2 2 1 1 460 500 1,09 - - 8,4 10,9 10
L3 2 1 2 230 500 2,17 - - 5,29 7,79 10
L4 2 1 1 110 460 4,18 0,50 25,00 8,8 11,3 10
𝜓2 𝜓3
𝑑𝑒𝑠𝑡 =
𝑙𝑥
𝜓2. 𝜓3
ቊ
𝑙𝑥
0,7 ∙ 𝑙𝑦
𝑙∗ ≤

55. Laje L4 em balanço com mureta na extremidade, sem outras paredes:
Pinheiro et al. (2003)

56. • Carga permanente (G) e variável (Q) diretamente sobre a laje:
• Carga da mureta (1,1 m de altura):
• Reação e momento devido a mureta:
𝐺 = 𝐺𝑝𝑝 + 𝐺𝑠𝑜𝑏𝑟𝑒𝑐𝑎𝑟𝑔𝑎 = 𝐺𝑝𝑝 + 𝐺𝑝𝑖𝑠𝑜 𝑒 𝑟𝑒𝑣𝑒𝑠𝑡𝑖𝑚𝑒𝑛𝑡𝑜
𝐺 = 25
𝑘𝑁
𝑚3 ∙ 0,1𝑚 + 21
𝑘𝑁
𝑚3 ∙ 0,05𝑚 = 3,5 𝑘𝑁/𝑚²
Argamassa de cimento e
areia (tabela 1 da NBR 6120:2019)
de 5 cm de espessura
𝑄 = 3 𝑘𝑁/𝑚²
Ex: agências de bancos, hospitais e etc.
(tabela 10 da NBR 6120:2019)
Alvenaria de vedação de bloco cerâmico vazado
de 14 cm (tabela 10 da NBR 6120:2019)
𝐺𝑚 + 𝑄𝑚 = 1,9
𝑘𝑁
𝑚2 ∙ 1,1𝑚 + 2,0
𝑘𝑁
𝑚
= 4,09 Nota j da tabela 10 da NBR 6120:2019
𝑟 = 𝑃 ∙ 𝑙 + 𝐺𝑚 + 𝑄𝑚 = 6,5 ∙ 1,1 + 4,09 = 11,24 𝑘𝑁/𝑚
𝑃 = 𝐺 + 𝑄 = 6,5
𝑘𝑁
𝑚2
𝑚 =
𝑃 ∙ 𝑙²
2
+ 𝐺𝑚 + 𝑄𝑚 ∙ 𝑙 =
6,5 ∙ 1,12
2
+ 4,09 ∙ 1,1 = 8,43 𝑘𝑁.
𝑚
𝑚

57. Ações, Reações e Momentos Fletores
para lajes L1, L2 e L3.

58. Tipo lx (cm) ly (cm) λ=ly/lx Resist. (Mpa) P.P. (kN/m²)
Piso+revest.
(kN/m²)
Divisórias
(kN/m²) Mureta (kN/m)
L1 2B 380 690 1,8 25 2,5 1 1 -
L2 2A 460 500 1,09 25 2,5 1 1 -
L3 3 230 500 2,17 25 2,5 1 1 -
L4 2 110 460 4,18 25 2,5 1 - 4,09
g
(kN/m²)
q
(kN/m²)
p
(kN/m²) r (kN/m²)
m
(kN.m/m) vi x vi' x vi y vi' y v x v y v' x v' y
4,5 3 7,5 - - 3,45 5,05 1,83 - 9,86 5,21 14,45 -
4,5 3 7,5 - - 2,01 - 2,85 4,17 6,93 9,83 - 14,39
4,5 3 7,5 - - 4,38 6,25 2,17 3,17 7,55 3,74 10,78 5,47
3,5 3 6,5 11,24 8,43 - - - - - - - -
mi x mi' x mi y mi' y m x m y m' x m' y
5,75 11,84 1,68 - 6,23 1,82 12,88 -
3,61 - 3,74 9,18 5,73 5,94 - 14,57
7,03 12,5 1,6 8,2 2,78 0,63 4,96 3,25
- - - - - - - -

59. Fonte: Pinheiro (1994).
L1

60. Fonte: Pinheiro (1994).
L1

61. Representação das reações de apoio

62. Compatibilização de momentos
+𝑚2

63. Representação dos momentos fletores
ቐ
0,8 × 14,57 = 11,66
14,57 + 12,88
2
= 13,73
14,57 − 13,75
2
+ 5,94

64. Dimensionamento das
armaduras de lajes

65. Dimensionamento
• O cálculo de 𝐴𝑠 é realizado por metro linear
de laje (p/ cada 100 cm).
• Momento fletor de cálculo: 𝑚𝑑 = 𝛾𝑓 × 𝑚𝑘.
• Coeficiente para uso da tabela e cálculo de 𝐴𝑠:
𝑘𝑐 =
𝑏𝑤 × 𝑑2
𝑚𝑑
𝐴𝑠 =
𝑘𝑠 × 𝑚𝑑
𝑑
100 𝑐𝑚
Tabela
𝑘𝑠
Tabela N° de
barras
Adotar ∅

66. Fonte: PINHEIRO, 2004.

67. Fonte: PINHEIRO, 2004.

68. Fonte: PINHEIRO, 2004.

69. Dimensionamento
• Verificar armadura mínima:
• Taxa de armadura mínima calculada para o
momento mínimo (item 17.3.5.2.1 da NBR
6118:2023):
𝜌 = 𝐴𝑠 × (𝑏𝑤 × 𝑑)
𝑀𝑑,𝑚𝑖𝑛 = 0,8 ∙ 𝑊0 ∙ 𝑓𝑐𝑡𝑘,𝑠𝑢𝑝
𝑊0 → módulo de resistência da seção transversal bruta de concreto, relativo à fibra mais tracionada,
𝑊 =
𝑏.ℎ²
6
para seções retangulares.
Em todo o caso, respeitar a taxa mínima:
0,15 %

70. 𝐴𝑠,𝑚𝑎𝑥 = 4% × 𝐴𝑐
𝝆𝒎𝒊𝒏 (
𝑨𝒔,𝒎𝒊𝒏
𝑨𝒄
), valores em %
Seção 20 25 30 35 40 45 50 55 60 65 70
retangular 0,15 0,15 0,15 0,164 0,179 0,194 0,208 0,211 0,219 0,226 0,233
Fonte: Tabela 17.3 da NBR 6118:2022, adaptado.
𝝆𝒎𝒊𝒏 (
𝑨𝒔,𝒎𝒊𝒏
𝑨𝒄
), valores em %
Seção 80 85 90
retangular 0,245 0,251 0,256
Taxas mínimas de armadura de flexão
(Tabela 17.3 da NBR 6118:2022, adaptado)
Taxa máxima de armadura de flexão
(itens 19.3.3.3 e 17.3.5.2.4 da NBR 6118:2022, adaptado):

71. Armadura mínima
Elementos sem
armadura ativa
Armaduras negativas 𝜌𝑠 ≥ 𝜌𝑚𝑖𝑛
Armaduras negativas de bordas sem continuidade 𝜌𝑠 ≥ 0,67 ∙ 𝜌𝑚𝑖𝑛
Armaduras positivas de lajes armadas nas duas
direções
𝜌𝑠 ≥ 0,67 ∙ 𝜌𝑚𝑖𝑛
Armadura positiva (principal) de lajes armadas em
uma direção
𝜌𝑠 ≥ 𝜌𝑚𝑖𝑛
Armadura positiva (secundária) de lajes armadas
em uma direção
Maior entre:
𝐴𝑠
𝑠
≥ 20% da
armadura principal
𝐴𝑠
𝑠
≥ 0,9 cm²/m
𝜌𝑠 ≥ 0,5 ∙ 𝜌𝑚𝑖𝑛
Armaduras mínimas passivas para lajes. Fonte: Tabela 19.1 da ABNT NBR 6118:2022, adaptado.
Armaduras mínimas passivas para lajes

72. Considerações da NBR 6118:2022, item 20.1
• Qualquer barra da armadura de flexão deve ter diâmetro no
máximo igual a h/8.
• As barras da armadura principal de flexão devem apresentar
espaçamento no máximo igual a 2 h ou 20 cm, prevalecendo o
menor desses dois valores na região dos maiores momentos
fletores.
• A armadura secundária de flexão deve ser igual ou superior a 20 %
da armadura principal, mantendo-se, ainda, um espaçamento entre
barras de no máximo 33 cm. A emenda dessas barras deve respeitar
os mesmos critérios de emenda das barras da armadura principal.
• Os estribos em lajes nervuradas, quando necessários, não podem
ter espaçamento superior a 20 cm.

73. Espaçamento mínimo
• Não especificado para lajes pela NBR 6118:2022;
• Bastos (2015) recomenda que o espaçamento adotado não
dificulte a disposição e amarração das barras da armadura, o
completo preenchimento da peça pelo concreto e o
envolvimento das barras pelo concreto. Indica ainda que é
possível adotar os valores para as armaduras longitudinais das
vigas:
• O espaçamento a ser utilizado deve permitir a passagem do
vibrador.
ቐ
2 𝑐𝑚
𝜙𝑙
1,2 ∙ 𝑑𝑚𝑎𝑥

74. Exemplo de dimensionamento

75. Concreto: 𝐶25
Aço 𝐶𝐴 − 50 (∅ ≥ 6,3 𝑚𝑚)
Aço 𝐶𝐴 − 60 (∅ ≥ 5,0 𝑚𝑚)
𝑐 = 2 𝑐𝑚
Classe de agressividade Ambiental I
Dados:

76. Disposições construtivas
• Diâmetro:
– Diâmetro máximo:
– Recomenda-se, para o diâmetro mínimo:
– Adotado inicialmente:
∅𝑚𝑎𝑥 ≤
ℎ
8
=
10 𝑐𝑚
8
= 12,5 𝑚𝑚
∅𝑚𝑖𝑛 = 5 𝑚𝑚 (Pinheiro, 2004)
∅ = 10 𝑚𝑚
∅𝑚𝑖𝑛 = 6,3 𝑚𝑚 (Bastos, 2015)

77. Disposições construtivas
• Espaçamento:
– Espaçamento máximo:
• Armadura principal:
• Armadura secundária:
– Espaçamento mínimo:
𝑠𝑚𝑎𝑥 ≥ ቊ
2 × ℎ = 2 × 10 = 20 𝑐𝑚
20 𝑐𝑚
𝑠𝑚𝑎𝑥 = 33 𝑐𝑚
𝑠𝑚𝑖𝑛 = 10 𝑐𝑚

78. Armadura mínima
Elementos sem
armadura ativa
Armaduras negativas 𝜌𝑠 ≥ 𝜌𝑚𝑖𝑛
Armaduras negativas de bordas sem continuidade 𝜌𝑠 ≥ 0,67 ∙ 𝜌𝑚𝑖𝑛
Armaduras positivas de lajes armadas nas duas
direções
𝜌𝑠 ≥ 0,67 ∙ 𝜌𝑚𝑖𝑛
Armadura positiva (principal) de lajes armadas em
uma direção
𝜌𝑠 ≥ 𝜌𝑚𝑖𝑛
Armadura positiva (secundária) de lajes armadas
em uma direção
Maior entre:
𝐴𝑠
𝑠
≥ 20% da
armadura principal
𝐴𝑠
𝑠
≥ 0,9 cm²/m
𝜌𝑠 ≥ 0,5 ∙ 𝜌𝑚𝑖𝑛
Armaduras mínimas passivas para lajes. Fonte: Tabela 19.1 da ABNT NBR 6118:2019, adaptado.
Armaduras mínimas passivas para lajes

79. Armaduras mínimas
• P/𝜆 > 2:
– Negativa e positiva principais (𝜌𝑠 ≥ 𝜌𝑚𝑖𝑛 - tab. da norma):
– Negativa de distribuição e positiva secundária:
𝐴𝑠,𝑚𝑖𝑛 = 𝜌𝑚𝑖𝑛. 𝑏. ℎ = 0,0015.100.10 = 1,5𝑐𝑚2
/𝑚
𝐴𝑠,𝑚𝑖𝑛 = ൞
0,2. 𝐴𝑠,𝑝𝑟𝑖𝑛𝑐
0,5. 𝜌𝑚𝑖𝑛. 𝑏. ℎ = 0,15.1,5 = 0,75 𝑐𝑚2
/𝑚
0,9 𝑐𝑚2
/𝑚

80. Armaduras mínimas
• P/𝜆 ≤ 2:
– Negativa principal:
– Positivas (principal ou secundária):
– Negativa secundária:
𝐴𝑠,𝑚𝑖𝑛 = 𝜌𝑚𝑖𝑛. 𝑏. ℎ = 0,0015.100.10 = 1,5𝑐𝑚2
/𝑚
𝐴𝑠,𝑚𝑖𝑛 = 0,67. 𝜌𝑚𝑖𝑛. 𝑏. ℎ = 0,67.1,5 = 1,00𝑐𝑚2/𝑚
𝐴𝑠,𝑚𝑖𝑛 = ൞
0,2. 𝐴𝑠,𝑝𝑟𝑖𝑛𝑐
0,5. 𝜌𝑚𝑖𝑛. 𝑏. ℎ = 0,15.1,5 = 0,75 𝑐𝑚2/𝑚
0,9 𝑐𝑚2
/𝑚

81. Cálculo das armaduras
Já compatibilizados 1,4 ∙ 𝑚𝑘
Adotar conforme
condições de obra
൝
h = 𝑑𝑒𝑥𝑡𝑟𝑒𝑚𝑖𝑑𝑎𝑑𝑒 + c + (0,5 × ∅𝑒𝑥𝑡𝑟𝑒𝑚𝑖𝑑𝑎𝑑𝑒)
h = 𝑑𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡𝑒 + c + (∅𝑒𝑥𝑡𝑟𝑒𝑚𝑖𝑑𝑎𝑑𝑒 + 0,5 ∙ ∅𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡𝑒)
𝑘𝑐 =
𝑏𝑤 × 𝑑2
𝑚𝑑
𝐴𝑠 =
𝑘𝑠 × 𝑚𝑑
𝑑
Tabela 1.4a de
Pinheiro (1994)
Tabela 1.1 de Pinheiro (1994)
Tabela 17.3 da NBR 6118:2014 Tabela 19.1 da NBR 6118:2014
1,4 ∙ 𝛾𝑛 ∙ 𝑚𝑘

82. Fonte: Pinheiro (1994).
N8 - 𝜙 10 c/13

83. Cálculo de flechas em lajes

84. Verificação da existência de fissuras
• De acordo com o item 17.3.1 da NBR 6118:2014, no ELS, as
estruturas trabalham parcialmente nos estádios I e II e o
momento de fissuração (𝑀𝑟 ) define a separação desses
estádios:
• Em que:
𝑴𝒓 =
𝜶 ∙ 𝒇𝒄𝒕 ∙ 𝑰𝒄
𝒚𝒕
𝛂 Situação
1,2 Seções T ou duplo T
1,3 Seções I ou T invertido
1,5 Seções retangulares
𝜶
Fator que correlaciona aproximadamente a resistência
à tração na flexão vs. tração direta
𝒚𝒕
Distância do centro de gravidade da seção à fibra mais
tracionada
𝑰𝒄 Momento de inércia da seção bruta de concreto
𝒇𝒄𝒕
Resistência à tração direta do concreto, conforme
8.2.5 da NBR 6118:2014.

85. Verificação da existência de fissuras
• Considerando tratar-se de uma laje (de seção retangular) e
para concretos do grupo I, temos:
𝐼𝑐 =
𝑏 ∙ ℎ³
12
𝑓𝑐𝑡 = 𝑓𝑐𝑡,𝑚 = 0,3 ∙ 𝑓𝑐𝑘
2
3 (𝑓𝑐𝑘 ≤ 50 𝑀𝑃𝑎)
𝛼 = 1,5
𝑓𝑐𝑡 = 𝑓𝑐𝑡,𝑚 = 2,12 ∙ 𝑙𝑛 1 + 0,1 ∙ 𝑓𝑐𝑘 + 8 (𝑓𝑐𝑘 > 50 𝑀𝑃𝑎)
P/ calcular 𝑀𝑟, utilizar o 𝑓𝑐𝑡𝑘, inf no estado-limite de formação de fissuras e o
𝑓𝑐𝑡, 𝑚 no estado-limite de deformação excessiva.
𝑓𝑐𝑡𝑘,𝑖𝑛𝑓 = 0,7 ∙ 𝑓𝑐𝑡,𝑚

86. Verificação da existência de fissuras
• DETERMINAÇÃO DO ESTÁDIO (item 17.3.2.1 - NBR 6118):
– Será considerado o procedimento para cálculo de flechas em vigas.
– Caso 𝑀𝑠𝑜𝑙,𝑟𝑎𝑟𝑎 < 𝑀𝑎, não ocorrem fissuras e considera-se a seção do
no estádio I. A flecha é calculada apenas com o momento de inércia 𝐼𝑐.
– Do contrário, ocorrem fissuras, considera-se a seção do no estádio II e
calcula-se (𝐸𝐼)𝑒𝑞. A flecha é calculada considerando o 𝐸𝑐𝑠.
– Combinação rara (Tabela 11.4 da NBR 6118, item 11.8.3.2):
𝑭𝒅,𝒔𝒆𝒓 valor de cálculo das ações para combinações de serviço
𝑭𝒒𝟏𝒌 valor característico das ações variáveis principais diretas
𝝍𝟏 Fator de redução de combinação frequente para ELS (Tabela 11.4 da NBR 6118)
𝑴𝒔𝒐𝒍,𝒓𝒂𝒓𝒂 Momento fletor solicitante na combinação rara
𝑴𝒂 Momento fletor na seção crítica do vão considerado
𝐹𝑑,𝑠𝑒𝑟 = Σ𝐹𝑔𝑖𝑘 + 𝐹𝑞1𝑘 + Σ𝜓1𝑗𝐹𝑞𝑗𝑘

87. Ações 𝝍𝟎 𝝍𝟏 𝝍𝟐
Cargas
acidentais de
edifícios
Locais em que não há predominância de pesos de
equipamentos que permanecem fixos por longos períodos de
tempo, nem de elevadas concentrações de pessoas
0,5 0,4 0,3
Locais em que há predominância de pesos de equipamentos
que permanecem fixos por longos períodos de tempo, ou de
elevada concentração de pessoas
0,7 0,6 0,4
Biblioteca, arquivos, oficinas e garagens 0,8 0,7 0,6
Vento Pressão dinâmica do vento nas estruturas em geral 0,6 0,3 0
Temperatura
Variações uniformes de temperatura em relação à média
anual local
0,6 0,5 0,3
Tabela 11.2 da NBR 6118:2023 - Valores do coeficiente 𝛾𝑓2
• DETERMINAÇÃO DO ESTÁDIO (item 17.3.2.1 - NBR 6118):
Verificação da existência de fissuras

88. Verificação da existência de fissuras
• FLECHA IMEDIATA:
– Ocorre quando são aplicados os carregamentos iniciais;
– Calcula-se a rigidez equivalente (item 17.3.2.1.1 da NBR 6118:2023):
(𝐸𝐼)𝑒𝑞,𝑡0= 𝐸𝑐𝑠
𝑀𝑟
𝑀𝑎
3
𝐼𝑐 + 1 −
𝑀𝑟
𝑀𝑎
3
𝐼𝐼𝐼 ≤ 𝐸𝑐𝑠𝐼𝑐
𝑰𝒄 Momento de inércia da seção bruta de concreto.
𝑰𝑰𝑰 Momento de inércia da seção fissurada de concreto no estádio II, calculado com 𝛼𝑒 =
𝐸𝑠
𝐸𝑐𝑠
.
𝑴𝒂
Momento fletor na seção crítica do vão considerado (momento máximo para vigas biapoiadas e
contínuas e momento no apoio para balanços).
𝑴𝒓
Momento de fissuração do elemento estrutural, cujo valor deve ser reduzido à metade no caso
de utilização de barras lisas.
𝑬𝒄𝒔 Módulo de elasticidade secante do concreto.

89. Verificação da existência de fissuras
• Caso seja necessária uma maior precisão para vigas continuas,
é permitido adotar um valor ponderado para a rigidez
equivalente:
(𝐸𝐼)𝑒𝑞=
1
𝑙
(𝐸𝐼)𝑒𝑞,1× 𝑎1 + (𝐸𝐼)𝑒𝑞,𝑣× 𝑎𝑣 + (𝐸𝐼)𝑒𝑞,2× 𝑎2
(𝐸𝐼)𝑒𝑞,1 é a rigidez equivalente do trecho 1
(𝐸𝐼)𝑒𝑞,𝑣 é a rigidez equivalente do trecho de momentos positivos
(𝐸𝐼)𝑒𝑞 é a rigidez equivalente do trecho 2
onde:
𝑎1/𝑙 e 𝑎2/𝑙 podem ser considerados iguais a 0,15, por aproximação.

90. Verificação da existência de fissuras
• FLECHA IMEDIATA:
– Caso ocorra estádio I (𝑓𝑐𝑘 ≤ 50 𝑀𝑃𝑎): não é necessário calcular
(𝐸𝐼)𝑒𝑞,𝑡0. Sendo assim, temos:
𝐸𝐼 = 𝐸𝑐𝑠𝐼𝑐
𝐼𝑐 =
𝑏 ∙ ℎ³
12
𝐸𝑐𝑠 = 𝛼𝑖𝐸𝑐𝑖
𝛼𝑖 = 0,8 + 0,2
𝑓𝑐𝑘
80
≤ 1,0

91. Verificação da existência de fissuras
• FLECHA IMEDIATA:
– Equações para cálculo da linha neutra e 𝐼2 no estádio II (𝑓𝑐𝑘 ≤
50 𝑀𝑃𝑎):
𝑏
2
∙ 𝑥2
2
+ 𝛼𝑒 ∙ 𝐴′
𝑠 ∙ (𝑥2 − 𝑑′) − 𝛼𝑒 ∙ 𝐴𝑠 ∙ (𝑑 − 𝑥2) = 0
𝐼2 =
𝑏 ∙ 𝑥2³
3
+ 𝛼𝑒 ∙ 𝐴𝑠 ∙ 𝑑 − 𝑥2
2 + 𝛼𝑒 ∙ 𝐴′
𝑠 ∙ (𝑥2 − 𝑑′)²

92. Verificação da existência de fissuras
• FLECHA IMEDIATA:
– Para 𝜆 ≤ 2,0, utilizar coeficientes 𝛼 de Pinheiro (1994) e a equação
para a flecha imediata (𝑎𝑖):
– Flecha total (𝑎𝑡 ):
𝑎𝑖 =
𝛼 ∙ 𝑏 ∙ 𝑝 ∙ 𝑙𝑥
4
1200 ∙ 𝐸𝐼
𝜶 Coeficiente tabelado em função de 𝜆 ou 𝛾
𝒃 Largura da seção
𝑬𝑰 Rigidez da laje à flexão
𝒑 carregamento para combinação quase permanente
𝒍𝒙 Menor vão
𝑎𝑡 = 𝑎𝑖(1 + 𝛼𝑓)

93. Verificação da existência de fissuras
• FLECHA IMEDIATA:
– Para 𝜆 > 2,0 e carga distribuída uniformemente:
• Biapoiada:
• Apoio do tipo engaste-simples:
• Apoio do tipo engaste-engaste:
𝑎𝑖 =
5 ∙ 𝑝 ∙ 𝑙𝑥
4
384 ∙ 𝐸𝐼
𝑎𝑖 =
𝑝 ∙ 𝑙𝑥
4
185 ∙ 𝐸𝐼
𝑎𝑖 =
𝑝 ∙ 𝑙𝑥
4
384 ∙ 𝐸𝐼

94. Verificação da existência de fissuras
• FLECHA DIFERIDA:
– Está relacionada ao efeito da fluência que ocorre devido a
carregamentos que atuam na estrutura ao longo do tempo (NBR
6118:2014, item 17.3.2.1.2).
𝝃 coeficiente função do tempo - Tabela 17.1 da NBR 6118:2014 ou das expressões a seguir
𝒕𝟎 Idade, em meses, relativa à data de aplicação da carga de longa duração
𝛼𝑓 =
Δ𝜉
1 + 50 ∙ 𝜌′
𝜌′ =
𝐴′𝑠
𝑏 ∙ 𝑑
𝑡0 =
σ 𝑃𝑖𝑡0𝑖
σ 𝑃𝑖
𝑃𝑖 são as parcelas de carga e 𝑡0𝑖 é a idade em que se aplica cada 𝑃𝑖.

95. Verificação da existência de fissuras
• FLECHA DIFERIDA:
Δ𝜉 = 𝜉 𝑡 − 𝜉(𝑡0)
𝜉 𝑡 = 0,68 ∙ 0,996𝑡
∙ 𝑡0,32
para 𝑡 ≤ 70 meses
𝜉 𝑡 = 2 para 𝑡 > 70 meses
Tempo (t) em meses 0 0,5 1 2 3 4 5 10 20 40 ≥70
Coeficiente ξ(t) 0 0,54 0,68 0,84 0,95 1,04 1,12 1,36 1,64 1,89 2
Valores do coeficiente ξ em função do tempo. Fonte: Tabela 17.1 da NBR 6118:2014, adaptado.

96. P/ existência de fissuras
• Estádio I (𝑓𝑐𝑘 ≤ 50 𝑀𝑃𝑎):
𝑥1 =
𝑏 ∙ ℎ²
2
+ (𝛼𝑒 − 1) ∙ 𝐴𝑠 ∙ 𝑑
𝑏 ∙ ℎ + (𝛼𝑒 − 1) ∙ 𝐴𝑠
𝐼1 =
𝑏 ∙ ℎ³
12
+ 𝑏 ∙ ℎ ∙ 𝑥1 −
ℎ
2
2
+ (𝛼𝑒 − 1) ∙ 𝐴𝑠 ∙ (𝑑 − 𝑥1)²

97. Fonte: Pinheiro (1994)

98. Tipo de efeito
Razão da
limitação
Exemplo
Deslocamento a
considerar
Deslocamento-limite
Aceitabilidade
sensorial
Visual
Deslocamentos visíveis
em elementos
estruturais
Total L/250
Outro
Vibrações
sentidas no piso
Devido a cargas
acidentais
L/350
Efeitos
estruturais em
serviço
Superfícies que
devem
drenar água
Coberturas e
varandas
Total L/250
Pavimentos que
devem
permanecer
planos
Ginásios e
pistas de
boliche
Total L/350+contraflecha
Ocorrido após a
construção do piso
L/600
Elementos que
suportam
equipamentos
sensíveis
Laboratórios
Ocorrido após
nivelamento do
equipamento
De acordo com recomendação do
fabricante do equipamento
Efeitos em
elementos não
estruturais
Paredes
Alvenaria, caixilhos e
revestimentos
Após a construção
da parede
L/500 e 10 mm e θ=0,0017 rad
Divisórias leves e
caixilhos telescópicos
Ocorrido após a
instalação da divisória
L/250 e 25 mm
Movimento lateral de
edifícios
Provocado pela ação do
vento para combinação
frequente (y1 = 0,30)
H/1700 e Hi/850 entre pavimentos
Movimentos térmicos
verticais
Provocado por diferença
de temperatura
L/400 e 15 mm
Limites para deslocamentos (Tabela 13.3 da NBR 6118:2014, adaptado).

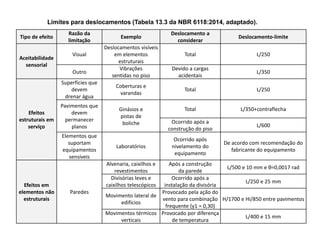
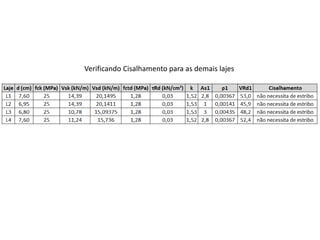
99. Verificação de força cortante
• NBR 6118:2023, item 19.4.
• lajes maciças ou nervuradas, não necessitam de armadura
transversal devido à força cortante, quando esta, a uma
distância d da face do apoio, obedecer à expressão:
– Em que:
𝑉𝑠𝑑 ≤ 𝑉𝑅𝑑1
𝑉𝑅𝑑1 = [𝜏𝑅𝑑 ∙ 𝑘 ∙ 1,2 + 40 ∙ 𝜌1 + 0,15 ∙ 𝜎𝑐𝑝] ∙ 𝑏𝑤 ∙ 𝑑
𝜏𝑅𝑑 = 0,25 ∙ 𝑓𝑐𝑡𝑑
𝑓𝑐𝑡𝑑 =
𝑓𝑐𝑡𝑘,𝑖𝑛𝑓
𝛾𝑐
𝜌1 =
𝐴𝑠1
𝑏𝑤 ∙ 𝑑
≤ 0,02
𝜎𝑐𝑝 =
𝑁𝑠𝑑
𝐴𝑐

100. Verificação de força cortante
– k é um coeficiente que tem os seguintes valores:
• Para elementos onde 50 % da armadura inferior não
chega até o apoio: k = |1|;
• Para os demais casos: k = | 1,6 − d |, não menor que | 1
|, com d em metros;
𝝉𝑹𝒅 tensão resistente de cálculo do concreto ao cisalhamento
𝒃𝒘 largura mínima da seção ao longo da altura útil d
𝑨𝒔𝟏
área da armadura de tração que se estende até não menos que d + lb,nec
além da seção considerada
𝑵𝒔𝒅 força longitudinal na seção devida à protensão ou carregamento

101. Continuação do exemplo

102. Verificando Cisalhamento
𝑉𝑠𝑑 = 1,4 𝑉𝑠𝑘 = 1,4 . 14,45 = 20,23 𝑘𝑁/𝑚
𝑉𝑅𝑑1 = 𝜏𝑅𝑑. 𝑘. 1,2 + 40. 𝜌1 . 𝑑
𝜏𝑅𝑑 = 0,25. 𝑓𝑐𝑡𝑑 = 0,25.
0,21. 𝑓𝑐𝑘
2/3
1,4
= 0,25.
0,1795
1,4
= 0,0321 𝑘𝑁/𝑐𝑚²
𝑘 = 1,6 − 0,076 = 1,524 𝑚 > 1 𝑚
𝑑 = 7,6 𝑐𝑚
P/ Laje L1, considerando a maior cortante:

103. Verificando Cisalhamento
• P/ Laje L1, considerando a maior cortante:
𝜌1 =
𝐴𝑠1
𝐴𝑐
=
2,79
100 . 7,6
= 0,367% < 0,02
𝑉𝑅𝑑1 = 0,0321 . 1,524 . 1,2 + 40 . 0,00367 . 100 . 7,6 = 50,07 𝑘𝑁/𝑚
𝑉𝑠𝑑 = 20,23 𝑘𝑁/𝑚 < 50,07𝑘𝑁/𝑚
𝑳𝒂𝒋𝒆 𝒏ã𝒐 𝒏𝒆𝒄𝒆𝒔𝒔𝒊𝒕𝒂 𝒅𝒆 𝒂𝒓𝒎𝒂𝒅𝒖𝒓𝒂 𝒕𝒓𝒂𝒏𝒔𝒗𝒆𝒓𝒔𝒂𝒍‼

104. Verificando Cisalhamento para as demais lajes

105. Verificando flechas
• P/ Laje L2 (verificando estádio):
𝑀𝑟 =
𝛼 ∙ 𝑓𝑐𝑡 ∙ 𝐼𝑐
𝑦𝑡
=
1,5 ∙ 0,26 ∙ 8.333,3
5
= 641,24 𝑘𝑁. 𝑐𝑚/𝑚
𝛼 = 1,5 (retangular)
𝑓𝑐𝑡 = 𝑓𝑐𝑚 = 0,3. 𝑓𝑐𝑘
2/3
= 0,3. 252/3
= 0,26 𝑘𝑁/𝑐𝑚²
𝐼𝑐 =
𝑏 ∙ ℎ³
12
=
100 ∙ 10³
12
= 8.333,3 𝑐𝑚4
𝑦𝑡 =
ℎ
2
=
10
2
= 5

106. Verificando flechas
• P/ Laje L2 (verificando estádio):
𝑀𝑟 = 641,24 𝑘𝑁.
𝑐𝑚
𝑚
≥ 𝑀𝑠𝑜𝑙, 𝑟𝑎𝑟𝑎 = 636 𝑘𝑁.
𝑐𝑚
𝑚
Estádio I
Não é necessário o cálculo de 𝐸𝐼𝑒𝑞

107. Verificando flechas
• P/ Laje L2 (flecha imediata):
𝑎𝑖 =
𝛼 ∙ 𝑏 ∙ 𝑝 ∙ 𝑙𝑥
4
1200 ∙ 𝐸𝐼
=
4,02 ∙ 100 ∙ 5,4 ∙ 10−4 ∙ 4604
12.000 ∙ 2.380 ∙ 8.333,3
= 0,41 𝑐𝑚
𝛼 = 4,02
𝑏 = 100 𝑐𝑚
𝑝 = 𝑔 + 𝜓 ∙ 𝑞 = 4,5 + 0,3 ∙ 3 = 5,4 𝑘𝑁/𝑚² = 5,4 ∙ 10−4
𝑘𝑁/𝑐𝑚2
𝐸𝑐𝑠 = 0,85 ∙ 5600 ∙ 25 = 2.380 𝑘𝑁/𝑐𝑚²
𝐼𝑐 = 8.333,3 𝑐𝑚4
𝑙𝑥 = 460 𝑐𝑚

108. Verificando flechas
• P/ as demais lajes:

109. Verificando flechas
• P/ Laje L2 (flecha diferida):
𝛼𝑓 =
Δ𝜉
1 + 50 ∙ 𝜌′
=
1,32
1 + 0
= 1,32
𝜌′
=
𝐴′𝑠
𝑏 ∙ 𝑑
=
0
𝑏 ∙ 𝑑
= 0
Tempo (t) em meses 0 0,5 1 2 3 4 5 10 20 40 ≥70
Coeficiente ξ(t) 0 0,54 0,68 0,84 0,95 1,04 1,12 1,36 1,64 1,89 2
Valores do coeficiente ξ em função do tempo. Fonte: Tabela 17.1 da NBR 6118:2014, adaptado.
Δ𝜉 = 2 − 0,68 = 1,32
Armadura de compressão = 0

110. Verificando flechas
• P/ Laje L2 (flecha total):
𝑎𝑖 ∙ 1 + 𝛼𝑓 = 0,41 ∙ 1 + 1,32 = 0,95 𝑐𝑚
𝑎𝑖 <
𝑙𝑥
250
=
460
250
= 1,84 𝑐𝑚 → 𝑶𝑲‼
Tipo de efeito
Razão da
limitação
Exemplo
Deslocamento a
considerar
Deslocamento-limite
Aceitabilidade
sensorial
Visual
Deslocamentos visíveis
em elementos
estruturais
Total L/250
Outro
Vibrações
sentidas no piso
Devido a cargas
acidentais
L/350

111. Referências Bibliográficas
• NBR-6118 – “Projeto e Execução de Obras de Concreto
Armado”, ABNT, 2014.
• NBR-6120 – “Cargas para o Cálculo de Estruturas de
Edificações”, ABNT, 2003.
• BASTOS, P. S. S. Estruturas de Concreto Armado. Notas de
Aula. 2014.
• PINHEIRO, L. M.; MUZARDO, C. D.; SANTOS, S. P. Fundamentos
de Concreto e Projeto de Edifícios. Notas de Aula. 2004.
• Chamberlain, Z. - Exemplo de um Projeto Completo de um
Edifício de Concreto Armado. Notas de Aula. 2001.