1. O documento é uma apostila sobre dimensionamento de estruturas de concreto armado que aborda tópicos como pilares, torção, punção, lajes e fundações.
2. Pilares são elementos verticais sujeitos principalmente a compressão, mas também à flexão, cisalhamento e instabilidade. São classificados quanto à posição e esbeltez, sendo esta relacionada à possibilidade de flambagem.
3. O dimensionamento de pilares envolve verificar seções, armaduras longitudinal e transversal, considerando imperfeições, excentric









![10
de terem os coeficientes de ponderação das ações majorados.
1.6. CRITÉRIOS DE DIMENSIONAMENTO
A NBR 6118/2014 não admite pilares com índice de esbeltez λ superior a 200,
exceto no caso de elementos pouco comprimidos, com força normal menor que 0,10 fcdAc.
Para pilares com índice de esbeltez maior ou igual a 140, na análise de 2ª ordem, devem-
se multiplicar os esforços solicitantes finais de cálculo por um coeficiente adicional:
]4,1/)140(01,0[11 n
A esbeltez limite (λ1) corresponde ao valor da variável que a partir do qual os
efeitos de 2ª ordem provocam uma redução da capacidade resistente do pilar no estado
limite último, quando comparada com a capacidade resistente obtida de acordo com a
teoria de 1ª ordem. Essa redução é definida arbitrariamente, não devendo ser superior a
10%, segundo a NBR 6118/2014.
O valor de 1 pode ser calculado pela expressão:
b
h
e
1
1
5,1225
onde 35 1 90
e1/h é a excentricidade relativa de 1ª ordem na extremidade do pilar onde ocorre
o momento de 1ª ordem de maior valor absoluto. Com os diagramas de esforços normais
e de momentos fletores em cada tramo do pilar, calculam-se as excentricidades iniciais
no topo e na base, dividindo-se o valor do momento pela força axial.
N
M
e
topo
topoi , e
N
M
e base
basei , (excentricidades iniciais)
h é a dimensão da seção na direção considerada.
Com relação ao parâmetro b temos as seguintes considerações a serem feitas:
a) Para pilares biapoiados sem carga horizontal, com pelo menos um dos momentos
que atuam nas extremidades do pilar sendo maior que o momento mínimo:
14,0,40,040,060,0 b
A
B
b sendo
M
M
Onde MA e MB são os momentos de 1ª ordem nos extremos do pilar, obtidos na
análise de 1ª ordem no caso de estruturas de nós fixos e os momentos totais (1ª ordem e
2ª ordem global) no caso de estruturas de nós móveis. Deve ser adotado para MA o maior](https://image.slidesharecdn.com/apostilaconcretoarmado2-170424130445/85/Apostila-de-Concreto-Armado-2-10-320.jpg)























![35
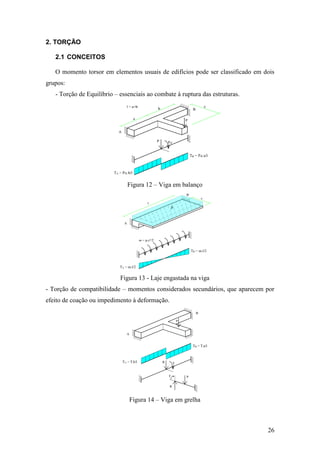
3. PUNÇÃO
Figura 18 – Panorama da fissuração em uma laje puncionada
3.1 COMPORTAMENTO DE LAJES SOB CARGA DE PUNÇÃO
Com relação ao comportamento das lajes sob o carregamento de punção, os ensaios
mostram que as deformações circunferenciais são inicialmente maiores que as
deformações radiais [Leonhardt e Mönnig (1979)]. Por isso, as fissuras radiais surgem
em primeiro lugar. Somente no ato do colapso há formação de uma fissura quase circular,
que limita o contorno de um sólido deslocado ao redor do pilar. Segundo CORDOVIL
(1997), a distância dessa fissura circular indica até onde a superfície de ruptura se estende.
Em lajes sem armadura de cisalhamento, essa superfície atinge distâncias que variam
entre duas a três vezes a altura útil d da laje, como ilustra a figura 19. O sólido deslocado
tem a semelhança de um tronco de cone, entretanto, com uma irregularidade acentuada.
Figura 19 – Zona de ruptura em lajes submetidas à punção, sem armadura transversal
CORDOVIL (1997) ressalta ainda que, no caso de lajes com armadura de
cisalhamento, a superfície de ruptura pode ocorrer em três posições diferentes:
- na zona entre o pilar e a primeira camada da armadura de cisalhamento, com
ruptura somente do concreto adjacente ao pilar (punção restrita);](https://image.slidesharecdn.com/apostilaconcretoarmado2-170424130445/85/Apostila-de-Concreto-Armado-2-35-320.jpg)