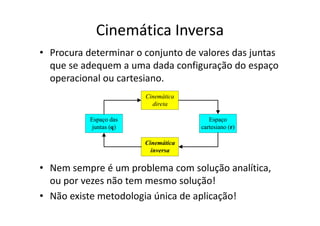
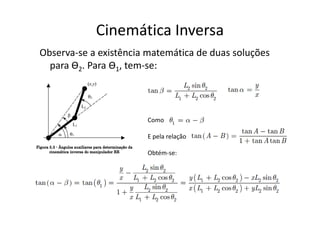
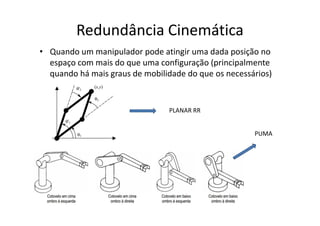
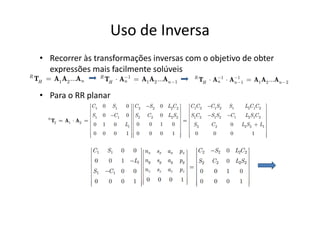
A aula aborda a cinemática inversa de manipuladores seriais, que determina os valores das juntas para uma configuração no espaço operacional. A cinemática inversa nem sempre tem solução analítica e pode haver múltiplas soluções ou degeneração. Exemplos incluem cinemática inversa de manipuladores planares RR e situações de redundância cinemática.

1. ROBÓTICA (ROB74) – AULA 4
CINEMÁTICA INVERSA DE
MANIPULADORES SERIAIS
PROF.: Michael Klug

2. PROGRAMA
• CINEMÁTICA DIRETA DE MANIPULADORES
SERIAIS
– Espaços das juntas e espaço cartesiano
– O algoritmo da cinemática direta– O algoritmo da cinemática direta
– Os 4 parâmetros de elos e juntas
• Denavit-Hartenberg
– Transformação associada a um elo

3. Cinemática Inversa
• Procura determinar o conjunto de valores das juntas
que se adequem a uma dada configuração do espaço
operacional ou cartesiano.
• Nem sempre é um problema com solução analítica,
ou por vezes não tem mesmo solução!
• Não existe metodologia única de aplicação!

4. • Exemplo: Manipulador RR no Plano
Cinemática Inversa
• Partindo das equações da cinemática direta, tem-se:

5. Elevando os termos ao quadrado
E sucessivamente
Cinemática Inversa
E sucessivamente

6. Observa-se a existência matemática de duas soluções
para Ө2. Para Ө1, tem-se:
Cinemática Inversa
Como
E pela relação
Obtém-se:

7. • Exemplo: Manipulador RR no espaço
Cinemática Inversa
Dos elementos relativos a px e py (posição), acha-se Ө1
A obtenção de Ө2 pode ser imediata se considerarmos as componentes de
orientação, bastando atender a nz e sz e o arctg do seu quociente, ou com
base no termo pz, tem-se
OBS: limitações de precisão numérica, o
ideal seria o uso da função arco-tangente

8. • Quando um manipulador pode atingir uma dada posição no
espaço com mais do que uma configuração (principalmente
quando há mais graus de mobilidade do que os necessários)
Redundância Cinemática
PLANAR RRPLANAR RR
PUMA

9. • Para um número infinito de configurações para uma dada
posição da mão diz-se que se atingiu uma situação de
degeneração.
• Ex: Robô RR planar de elos iguais para a mão no ponto (0,0),
ou situação em que o punho do robô fique com dois eixos
colineares e alinhados
Redundância Cinemática
colineares e alinhados

10. • Recorrer às transformações inversas com o objetivo de obter
expressões mais facilmente solúveis
• Para o RR planar
Uso de Inversa

11. Uso de Inversa
Tentando recorrer apenas a termos de posição, tem-se
Admitindo que Ө1 já tenha sido obtido anteriormente, obtém-se:

12. • Exemplo:
Relação Usual
OBS: apesar da dificuldade de obtenção da cinemática
inversa para casos gerais, a maioria dos manipuladores
industriais possuem soluções que são facilmente
encontradas na literatura.

13. • 3 DOF (GdL)
Punho Esférico

14. • Comparando os termos com a matriz de transformação geral para orientação
Punho Esférico
obtém-se

15. • Desacoplamento entre posição e orientação
Manipuladores com Punho Esférico
Olhar exemplos na literatura!!!